GSEB Solutions Class 12 Chemistry Chapter 1 The Solid State

Gujarat Board GSEB Textbook Solutions Class 12 Chemistry Chapter 1 The Solid State Textbook Questions and Answers, Additional Important Questions, Notes Pdf.

Gujarat Board Textbook Solutions Class 12 Chemistry Chapter 1 The Solid State

GSEB Class 12 Chemistry The Solid State InText Questions and Answers

Question 1.
Why are solids rigid?
Answer:
In solids, the constituent particles (atoms/ions/molecules) are held together by strong inter atomic or inter ionic or inter molecular attractive forces and hence solids are rigid.

Question 2.
Why do solids have a definite volume?
Answer:
In solids, the constituent particles are bound together by strong attractive forces and the interparticle distances remain unchanged at a given temperature. Thus, the solids have a definite volume.

Question 3.
Classify the following as amorphous or crystalline solids:
Polyurethane, naphthalene, benzoic acid, Teflon, potassium nitrate, cellophane, polyvinyl chloride, fiberglass, copper?
Answer:
Ionic – (NH₄)₃PO₄ and LiBr
Metallic – Brass and Rb
Molecular – P₄O₁₀,I₂ P₄
Network (Covalent) – Graphite, SiC, Si
Amorphous – Plastics

Question 4.
Why is glass considered a supercooled liquid?
Answer:
Like liquids, glass has a tendency to flow, though very slowly. Hence it is considered a supercooled liquid.

Question 5.
Refractive index of a solid is observed to have the same value along with all directions. Comment on the nature of this solid. Would it show cleavage property?
Answer:
Solid is amorphous because amorphous solids are isotropic in nature. No, it would not show the cleavage property.

Question 6.
Classify the following solids in different categories based on the nature of intermolecular forces operating in them:
Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide?
Answer:

1. Ionic solids: Potassium sulphate, zinc sulphide
2. Covalent solid: Graphite, silicon carbide
3. Molecular solid: Benzene, urea, ammonia, water, argon
4. Metallic solid: Rubidium, tin.

Question 7.
Solid A is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it?
Answer:
Covalent or network solid.

Question 8.
Ionic solids conduct electricity in molten state but not in solid state Explain?
Answer:
In Solid-state, ions are not free therefore ionic solids are bad conductors. However, in a molten state, the ions become free to conduct electric current.

Question 9.
What type of solids are electrical conductors, malleable and ductile?
Answer:
Metallic solids

Question 10.
Give the significance of a ‘lattice point’?
Answer:
Each lattice point represents one constituent particle of the solid. This constituent particle may be an atom, a molecule (group of atoms) or an ion.

Question 11.
Name the parameters that characterise a unit cell?
Answer:

1. Edge lengths along the three edges a, b and c.
2. Angles α, β and γ.

Question 12.
Distinguish between
1. Hexagonal and monoclinic unit cells
2. Face-centred and end-centered unit cells
Answer:

1. For Hexagonal unit cell, a = b ≠ c, α = β = 90°, γ = 120°.
   For monoclinic unit cell a ≠ b ≠ c, α = γ = 90°, β = 90°.
2. Face centred unit cell has pointed at the comers as well as the centre of each face. It has 4 atoms per unit cell.
   End centred unit cell has pointed at all the comers and at the centre of any two opposite faces. It has 2 atoms per unit cell.

Question 13.
Explain how many portions of an atom located at

1. corner and
2. body centre of a cubic unit cell is part of its neighbouring unit cell?

Answer:

1. 1/8th part of an atom located at comer belongs to neighbouring unit cell.
2. The atom at the body centre of a cubic unit cell is not shared by any other unit cell. Hence, it belongs fully to the unit cell.

Question 14.
What is the two-dimensional coordination number of a molecule in a square close-packed layer?
Answer:
Four

Question 15.
A compound forms a hexagonal close-packed structure. What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?
Answer:
An atom in hep structure has three voids, one octahedral and two tetrahedral.
Number of atoms in 0-5 mol = 0.5 × 6.022 × 10²³ = 3.011 × 10²³
Total number of voids = 3 × 3.011 × 10²³ = 9.033 × 10²³
Number of tetrahedral voids = 2 × 3.011 × 10²³ = 6.022 × 10²³.

Question 16.
A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy \(\frac{1}{3}\) rd of tetrahedral voids. What is the formula of the compound?
Answer:
Let the number of N atoms = 1
Number of tetrahedral voids = 2
Since only \(\frac{2}{3}\) rd of these are occupied by the atoms of element M, the number of M atoms = M_4/3 N or M₄N₃

Question 17.
Which of the following lattices has the highest packing efficiency

1. simple cubic
2. body- centered cubic and
3. hexagonal close-packed lattice?

Answer:
hep (74%) > bcc (68%) > simple cubic (52.4%)

Question 18.
An element with a molar mass 2.7 × 10^-2 kg mol^-1 forms a cubic unit cell with an edge length 405 pm. If its density is 2.7 × 10²³ kg^-3, what is the nature of the cubic unit cell?
Answer:
d = 2.7 × 10³ kg^-3 m, a = 405 × 10^-12 m
N_A = 6.022 × 10²³, M = 2.7 × 10^-2

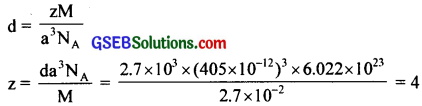
Since z = 4, the unit cell is fee or ccp.

Question 19.
What type of defect can arise when a solid is heated? Which physical property is affected by it and in what way?
Answer:
A vacancy defect is created when a solid is heated. This is because on the heating some atoms or ions leave the lattice site completely. As a result, the density of the substance decreases.

Question 20.
What type of stoichiometric defect is shown by:

1. ZnS
2. AgBr

Answer:

1. ZnS: Frenkel defect
2. AgBr: Schottky defect and Frenkel defect

Question 21.
Explain how vacancies are introduced in an ionic solid when a cation of higher valence is added as an impurity in it?
Answer:
When a cation of higher valency is added as an impurity in the ionic solid, some of the site of the original cations are occupied by the cations of higher valency. For example, Sr⁺² in NaCl. Each Sr⁺² replaces two Na⁺ ions. It occupies the site of one Na⁺ ion and the other site remains vacant. The cation vacancies thus produced are equal in number to that Sr⁺² ions.

Question 22.
Ionic solids, which have anionic vacancies due to metal excess defect, develop colour. Explain with the help of a suitable example?
Answer:
When ZnO is heated, the white colour turns to yellow because on heating, ZnO loses oxygen and there is excess of zinc in the crystal. The excess Zn²⁺ ions move to interstitial sites and the electrons to the nearest interstitial sites. These electrons can absorb visible light and impart yellow colour to ZnO.

Question 23.
A group 14 element is to be converted into n-type semiconductor by doping it with a suitable impurity. To which group should this impurity belong?
Answer:
In n-type semiconductors, electrons are the charge carriers and hence the impurity should be electron rich. Hence the impurity should belong to group-15.

Question 24.
What type of substances would make better permanent magnets, ferromagnetic or ferrimagnetic? Justify your answer?
Answer:
Ferromagnetic substances would make better permanent magnets because when a ferromagnetic substance is placed in a magnetic field, the magnetic moments permanently align in one direction to give a strong magnetic effect.

GSEB Class 12 Chemistry The Solid State Text Book Questions and Answers

Question 1.
Define the term ‘amorphous’. Give a few examples of amorphous solids?
Answer:
In non-crystalline solids constituent particles like atoms, molecules or ions do,not have a definite ordered structure. These do not have a definite geometry, thus they are also known as pseudo solid.
Example: Glass, rubber, plastic.

Question 2.
What makes a glass different from a solid such as quartz? Under what conditions could quartz be converted into glass?
Answer:
Glass is an amorphous solid in which the particles have only short-range order. But quartz is crystalline i.e., the constituent particles have long-range order. On melting quartz by heating and then cooling it rapidly, long-range order is disturbed and it is converted into glass.

Question 3.
Classify each of the following solids as ionic, metallic, molecular, network (covalent) or amorphous?

1. Tetra phosphorus decoxide (P₄O₁₀)
2. Ammonium phosphate (NH₄)₃PO₄
3. SiC
4. I₂
5. P₄
6. Plastic
7. Graphite
8. Brass
9. Rb
10. LiBr
11. Si

Answer:
Ionic : (NH₄)3PO₄, LiBr
Metallic : Brass, Rb
Molecular : P₄O₁₀,I₂,P₄
Network : Graphite, SiC, Si
Amorphous : Plastics.

Question 4.

1. What is meant by the term ‘coordination number’?
2. What is the coordination number of atoms
   • In a cubic close-packed structure.
   • In a body-centered cubic structure.

Answer:

1. The number of nearest particles which is in direct contact with a particle in a close-packed structure is called the coordination number.
2. The coordination number of atoms
   • In a cubic close-packed structure is 12
   • In a body-centered cubic structure is 8.

Question 5.
How can you determine the atomic mass of an unknown metal if you know its density and the dimension of its unit cell? Explain?
Answer:
The edge length of a cubic crystal of a clement is taken as ‘a. Then the density can be calculated as follows.
Edge length of the unit cell = ‘a’
Density of unit cell, d =
Volume of the unit cell = a³
Mass of unit cell = Number of atoms in the unit cell × Mass of each atom = z × m
(For simple cubic z = 1, for body centred cubic z = 2 and for face centred cubic z = 4)

lf ’a’ is in cm and M in g, the density will be in g/cm³.

Question 6.
‘Stability of a crystal is reflected in the magnitude of its melting points’. Comment. Collect melting points of solid water, ethyl alcohol, diethyl ether and methane from a data book. What can you say about the intermolecular forces between these molecules?
Answer:
Higher the stability of the crystal system, greater is its melting point because large amount of energy is required to change the structure from an ordered crystal form to a random molten form.

• Water: 273 K (Because of H-bonding)
• Ethyl alcohol: 158 K (H-bonding is to a lesser extent than water)
• Diethyl ether: 157K (No H-bonds but have van der Waal’s forces of attraction)
• Methane: 90K (Weak van der Waal’s forces)

Question 7.
How will you distinguish between the following pairs of terms?

1. Hexagonal close-packing and cubic close-packing?
2. Crystal lattice and unit cell?
3. Tetrahedral void and octahedral void?

Answer:
1. During the formation of crystals, the constituent particles are closely packed. In close packing the maximum available space is occupied. The stability of the crystals depends on the extent of close packing. In close packing the solid particles are considered as identical spheres.

Close Packing in One Dimension:
There is only one way of arranging spheres in a one-dimensional close-packed structure, that is to arrange them in a close packing of spheres in row and touching each other.

Close packing in two dimensions:
The spheres can be arranged side b side touching each other in a row. In order to have efficient use of the space we can have two ways with respect to the first row to build a crystal plane.

(i) The spheres are arranged in such a way that the rows have both horizontal and vertical alignment. Here the spheres are found to form squares. This type of packing is called square close packing.

(ii) The spheres in every second row are placed in the depressions between the spheres of the first row. The spheres in the third row arc seated in the depressions between the spheres of the second row and so on. This gives hexagonal close packing of spheres.

In hexagonal close packing. particles are more closely packed than square close packing. If only one laver of spheres is to he packed, spheres select hexagonal close packing because it is more efficient. In this arrangement also there are a number of vacant spaces.

The vacant sites in close-packed structures are called voids. These are of two types. The vacant space surrounded by four touching spheres in a close-packed arrangement is called a tetrahedral void. In a close packing. the number of tetrahedral voids are double the number of spheres.

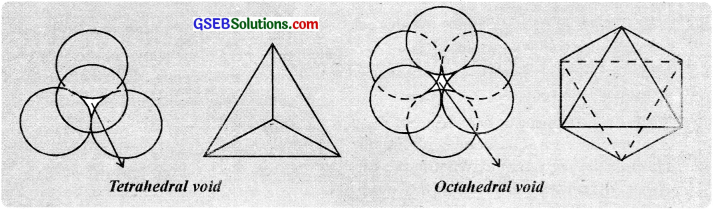
The vacant space surrounded by six spheres in a close packed arrangement is Called a octahedral void. In a close packing. the number of octahedral voids are equal to the number of spheres. The number of voids depend upon the number of close packed spheres. In a crystal having N particles.
the number of octahedral voids = N and
the number of tetrahedral voids = 2N

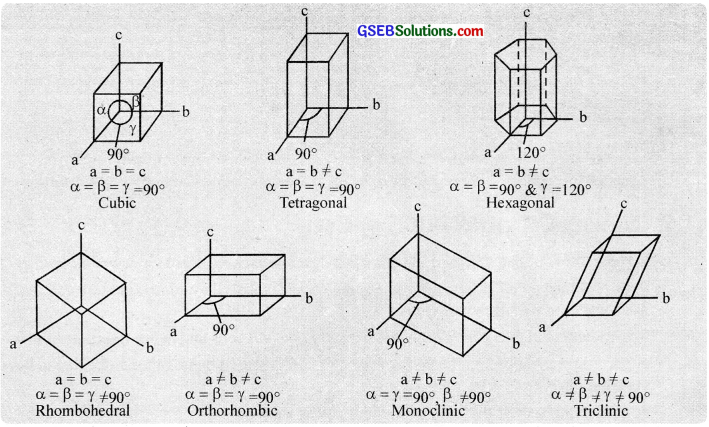
2. A crystal has an ordered internal arrangement of constituent particles such as atoms, ions or molecules in space. The three-dimensional arrangement of constituent particles in a crystal is known as crystal lattice or space lattice. There are only 14 three-dimensional lattices and are named as Bravais lattices. In a crystal lattice.
(i) Each point is called a lattice point or lattice site
(ii) Each point represents one constituent particle (particle may be atom, molecule or ion) and
(iii) Each point is joined by straight lines to bring out the geometry of the lattice.

A unit cell is the smallest repeating portion of the space lattice. A unit cell is characterised by the distances along with the three edges of the unit cell (a, b, c) and with the angle (α, β, γ) subtended between them. A careful examination of various types of crystals with their lattices indicates that there are seven types of basic unit cells or crystal systems. as given below.

3. (a) Covering tetrahedral voids:
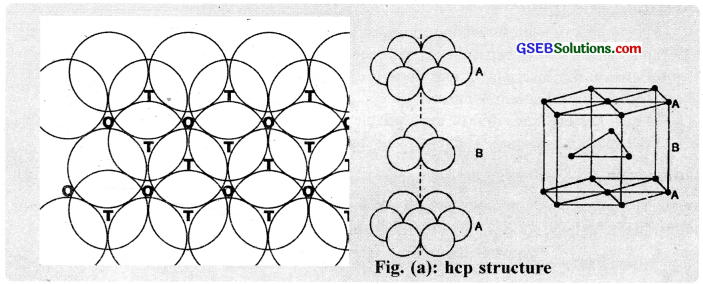
When the third layer ¡s placed above the second layer by covering the tetrahedral voids, the spheres of the third layer are aligned exactly like the first layer. Thus, the first, third, fifth etc. layers become identical. This type of packing is written as ABAB …………….. pattern and the structure is called hexagonal close-packed (hep) structure.
Mg, Zn. Cd etc possess hep structure.

(b) Covering octahedral voids:
When the third layer is placed above the second layer by covering the octahedral voids, a different arrangement as shon in figure (b) is obtained. Thus, the first, fourth, seventh etc. layers become identical. This type of packing is written as ABCABC …………………. pattern and the structure is called cubic close packed (ccp) or face centred cubic (fcc) structure. Cu. Ni, Au etc possess ccp arrangement.

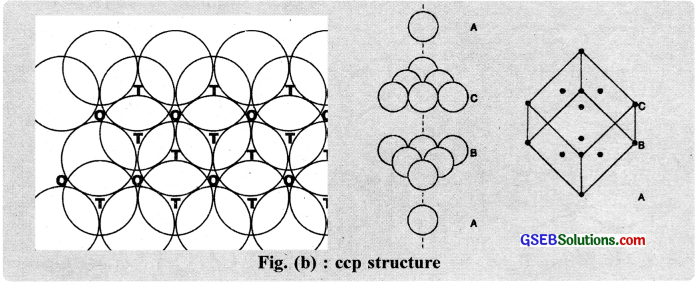
Question 8.
How many lattice points are there in one unit cell of each of the following lattices?

1. Face-centered cubic
2. Face-centred tetragonal
3. Body-centred

Answer:

1. z = 4
2. z = 4
3. z = 2

Question 9.
Explain?

1. The basis of similarities and differences between metallic and ionic crystals.
2. Ionic solids are hard and brittle.

Answer:
1. Metallic and Ionic crystal:
(a) Both metallic and ionic solids have high melting points.
(b) Ionic solids are hard and brittle but metallic solids are hard but not brittle, metals are malleable and ductile.
(c) Ionic solids are bad conductor but good conductor in a molten state and in solution. Metallic solids are good conductor in solid and liquid as well as in vapour state.
(d) Constituent units in ionic solids are cations and anions. In metallic solids, constituent units are Kernel (positively charged ions) surrounded by a sea of delocalized electrons.

2. Ionic crystals are hard because there are strong electrostatic forces of attraction among the oppositely charged ions. They are brittle because the ionic bond is non-directional.

Question 10.
Calculate the efficiency of packing in the case of a metal crystal for

1. simple cubic
2. body-centred cubic
3. face-centred cubic (with the assumptions that atoms are touching each other)

Answer:
1. In simple cubic, the atoms touch each other along the edges as shown in the figure.
The edge length of the unit cell is equal to 2r, e.. a = 2r
Simple unit cell contains only I atom

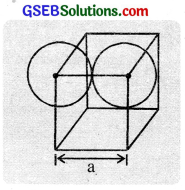
∴ Volume of spheres = \(\frac{4}{3}\) πr³
Volume of the unit cell = a³ (2r)³

2. In body centred cubic. the atoms touch each other along the body diagonal of the cube as shown in the figure.
The length of body diagonal is equal to 4r.
i.e., \(\sqrt{3a}\) = 4r
r = \(\frac{\sqrt{3}}{4}\) a

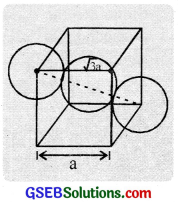
We know that each bec unit cell has 2 spheres.
∴ Total volume of 2 spheres = 2 × (\(\frac{4}{3}\)) πr³
Volume of the cube = a³ = (\(\frac{4 r}{\sqrt{3}}\))³
∴ Packing efficiency =

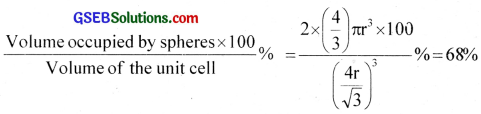
3. Both hcp and ccp are equally efficient. The ccp arrangement of spheres has face centred unit cells. In face centred cubic, the atoms touch each other along the face diagonals of the cube shown in the figure.
The length of the face diagonal is equal to 4r.
4r = \(\sqrt{2}\)a
a = \(\frac{4 r}{\sqrt{2}}\) = 2\(\sqrt{2}\)r (or r = \(\frac{\mathrm{a}}{2 \sqrt{2}}\))

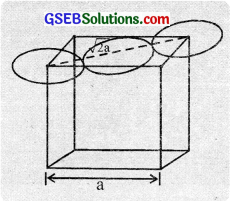
We know that each fcc unit cell has 4 spheres.
∴ Total olume of four spheres 4 × \(\frac{4}{3}\) πr³
Volume of the cube = a³ = (2\(\sqrt{2}\)r)³
Packing efficiency =

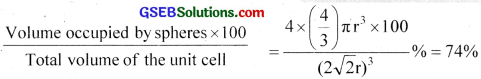
Question 11.
Silver crystallises in fee lattice. If edge length of the cell is 4.07 × 10^-8 cm and density is 10.5 g cm^-3, calculate the atomic mass of silver?
Answer:
a = 4.07 × 10^-8 cm, d = 10.5 gcm^-3, z = 4

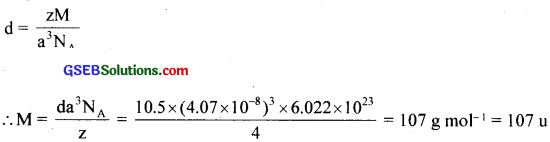
Question 12.
A cubic solid is made of.two elements, P and Q. Atoms of Q are at the comers of the cube and P at the body-centre. What is the formula of the compound? What are the coordination numbers of P and Q?
Ans.
Number of Q atoms = 8 × \(\frac{1}{8}\) = 1
Number of P atoms = 1
∴ The formula of the compound is PQ.
The coordination number of both P and Q is 8.

Question 13.
Niobium crystallises in body-centred cubic structure. If density is 8.55 g cm^-3, calculate atomic radius of niobium using its atomic mass 93 u?
Answer:
z = 2, d = 8.55 g cm^-3, M = 93u

Question 14.
If the radius of the octahedral void is r and radius of the atoms in close packing is R, derive relation between r and R?
Answer:
The radius, r of octahedral void = 0.414 R, where R is the radius of atoms in close packing.

Question 15.
Copper crystallises into a fee lattice with edge length 3.61 × 10^-8 cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm^-3.
Answer:
z = 4, M = 63.5 gmol^-1, a = 3.61 × 10^-8 cm

= 8.96 g cm^-3

Question 16.
Analysis shows that nickel oxide has the formula Ni₉₈O₁₀₀. What fractions of nickel exist as Ni²⁺ and Ni³⁺ ions?
Answer:
For 100 atoms of oxygen, there are 98 atoms of nickel.
If ‘x’ atoms of Ni are present as Ni²⁺, then the number of atoms of Ni³⁺ = 98 – x. Since the compound is electrically neutral, the total charge on 98 Ni ions should be equal to charge on 100 oxide (O^2-) ions.
Thus, (2 × X) + 3 × (98 – x) = 2 × 100
x = 94
∴ Fraction of Ni³⁺ = 0.04 0r 4%

Question 17.
What is a semiconductor? Describe the two main types of semiconductors and contrast their conduction mechanism?
Answer:

A substance whose conductance likes in between that of metals (Conductors) and insulators are called semiconductors. There are two main types of semiconductors :

(i) n-type semiconductors: Silicon and germanium belong to group 14 of the periodic table and have four valence electrons each. In their crystals each atom forms four covalent bonds with its neighbours. When doped with a group 15 element like P or As, which contains five valence electrons, they occupy some of the lattice sites in silicon or germanium crystal. Four out of five electrons are used in the formation of four covalent bonds with the four neighbouring silicon atoms. The fifth electron in extra and becomes delocalised.

These delocalised electrons increase the conductivity of doped silicon (or germanium). Here, the increase in conductivity is due to the negatively charged electron, hence silicon doped with electron with impurity is called n-type semiconductor.

(ii) p-type semiconductors: Silicon or germanium can also be doped with a group 13 element like B, A1 or Ga which contains only three valence electrons. The place where the fourth valence electron is missing is called electron-hole or electron vacancy. An electron from a neighbouring atom can come and fill the electron-hole, but in doing so it would leave an electron-hole at its original position.

If it happens it would appear as if the electron-hole has moved in the direction opposite to that of the electron that filled it under the influence of electric field, electrons would move towards the positively charged plate through electronic holes, but it would appear as if electron holes are positively charged and are moving towards the negatively charged plate. This type of semiconductors are called p-type semiconductors.The olids which have intermediate conductivities generally between 10^-6 to 10⁴ Ω^-1m^-1 are called semiconductors, e.g. Germanium and silicon. The two main types of semiconductors are as follows.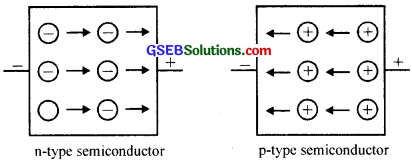

Question 18.
Non-stoichiometric cuprous oxide, Cu₂O can be prepared in laboratory. In this oxide, copper to oxygen ratio is slightly less than 2:1. Can you account for the fact that this substance is a p-type semiconductor?
Answer:
Since the copper to oxygen ratio is slightly less than 2:1, it means that Cu₂O has a metal deficiency defect. In such a crystal, when an electron moves from Cu⁺ to Cu²⁺ ion, a positive hole is created, which can move from one position to another. Thus current flow is due to the movement of positive holes and it is a p-type semiconductor.

Question 19.
Ferric oxide crystallises in a hexagonal close-packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of the ferric oxide?
Answer:
Number of oxide (O^2-) ions = n
Number of octahedral voids = n
Number of Fe³⁺ ions = \(\frac { 2 }{ 3 } \) n
Fe³⁺ : O^2- = \(\frac { 2 }{ 3 } \)n : n = 2 : 3
Formula, Fe₂O₃.

Question 20.
Classify each of the following as being either a p-type or an n-type semiconductor:

1. Ge doped with In
2. B doped with Si.

Answer:

1. p-type
2. n-type

Question 21.
Gold (atomic radius = 0.144 nm) crystallises in a face-centered unit cell. What is the length of a side of the cell?
Answer:
According to the question, r = 0.144 nm.
For fee structure:
Edge length (a) = 2\(\sqrt { 2 }\) × Radius of atom = 2 × 1.414 × 0.144 = 0.407 nm.

Question 22.
In terms of band theory, what is the difference

1. between a conductor and an insulator
2. between a conductor and a semiconductor?

Answer:
Based on their electrical conductivity, solids can be classified as,

• Conductors
• Insulators
• Semiconductors

(a) Conductors:
The solids through which electricity can flow to a large extent are called conductors. The electrical conductivity of metals is of the order of 10⁶ to 10⁸ ohm^-1 cm^-1.

(b) Insulators:
The solids which almost do not allow the passage of electricity are called insulators.
e.g. S, P, wood, rubber. The conductivity of insulators is of the order 10^-12 ohm^-1 cm^-1

(c) Semiconductors:
The solids whose conductivity lies between those of metallic conductors and insulators are called semiconductors. Their conductivity increases with increase in temperature. The conductivity of semiconductors lies in the range 10^-2 – 10^-9 ohm^-1 cm^-1. The conductivity of semiconductors increases with temperature while that of metals decreases with temperature.

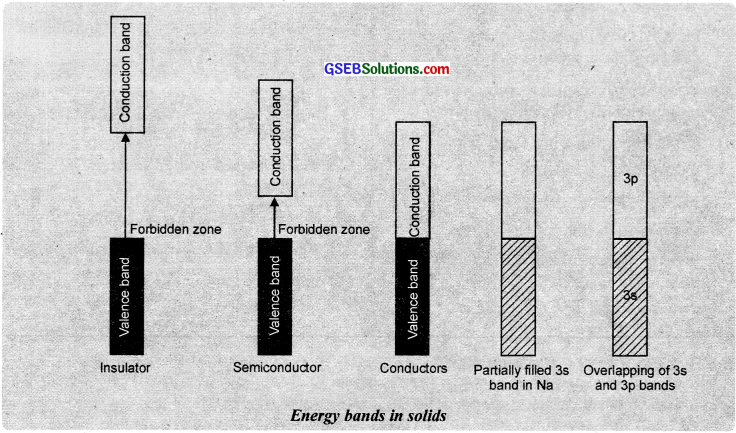
The conductivity of metals depends upon the number of valence electrons available per atom. The atomic orbitais of metal atoms form molecular orbitais which are so close in energy to each other as to form a band The bands formed by valence electrons are called the valence band (the highest occupied band) and the band just above the valence band formed by the orbitaIs of higher energy is called conduction band (the lowest unoccupied band).

In the case of metals, the valence band may be partially filled or there may be an overlapping between the valence and the conduction bands. This makes it possible for the electrons to go into the vacant bands and hence is responsible for the high electrical conductivity of metals. In the case of insulators, the energy gap (forbidden zone) is very large and therefore the vacant conduction band is not available to the electrons of the completely filled valence band.

In the case of semiconductors, the energy gap is very small and an increase in temperature gives thermal energy for some of the electrons in the valence band to move into the conduction band. Their electrical conductivity is in between that of insulators and conductors.

The electrical conductivity of semiconductors increases with rise in temperature because more electrons canjump to the conduction band. e.g. Si, Ge etc. The semiconductivity of these elements are due to the direct consequence of their structure and are known as intrinsic semiconductors. The semiconductivity of intrinsic semiconductors can be enhanced by the addition of small quantities of impurities and is known as extrinsic conduction. The prócess is called doping.

The group -15 elements of the periodic table such as P and As enter inside the crystal lattice of Ge or Si of group -14 by replacing them from the lattice points. The group -15 elements have one excess valence electron after forming the four covalent bonds. The excess electron gives rise to electronic conduction (n-type conduction). The group -13 elements like Al and Ga can also enter Ge or Si of group -14 substitutionally. Group -13 elements have only three valence electrons. They combine with group -14 elements to form an electron-deficient bond or a hole. They give rise to a positive hole
conduction [p-type conduction].

Group -14 elements doped with group -15 elements are called n-type semiconductors and group -14 elements doped with group -13 elements are called p-type semiconductors. This type of conduction due to the presence of impurities is known as extrinsic conduction.

The conducting ability of semiconductors and insulators is mainly determined by the impurities and defects in them. The oxides of transition metals exhibit wide variation in electrical conductivity.

Oxides like TiO. VO, ReO₃ etc. are good conductors. But oxides like Ti₂O₃, V₂O₃ etc. behave like insulators at certain temperatures. TiO₂, V₂O₅ etc are perfect insulators.

Applications of n-type and p-type semiconductors:
Various combinations of n-type and p-type semiconductors are used for making electronic components.

(a) Diode:
When p-type and n-type semiconductors are combined to form what ¡s known as p-n junction diode, it conducts electricity to flow only in one direction. Such a p-n junction is called a rectifier. It is used for converting alternating current into direct current.

(b) Transistors:
Transistors are made by sandwiching a layer of one type of semiconductor between two layers of other types of semiconductor. The NPN and PNP transistors thus formed are used to detect and amplify radio and audio signals.

Note: The solar cell is a photodiode which can convert light energy into electrical energy.

Question 23.
Explain the following terms with suitable examples:

1. Schottky defect
2. Frenkel defect
3. Interstitials and
4. F-centres.

Answer:
1. Schottky defect:
It arises due to the missing of an equal number of cations and anions from their normal positions leaving behind a pair of holes. This defect is usually observed in ionic compounds having a high co-ordination number and ions of almost similar size. The density of the crystal is lowered due to the presence of vacancies in the crystal lattice. Schottky defect increases slightly the electrical conductance of the crystal, e.g. NaCl, KCl, CsCl.

2. Frenkel defect:
It arises when an ion, usually cation, leaves its normal site and occupies an interstitial site This defect is usually observed in ionic compounds having a low co-ordination number and crystals with anions are much larger in size than the cations. Since no ions are missing from the crystal as a whole, it doesn’t affect the density of the crystal.
e.g. AgCl, ZnS, AgBr

3. Interstitials:
Atoms or ions which occupy the normally vacant interstitial positions in a crystal are called interstitials.

4. F-centres:
The electron occupying holes, created by the missing anions from the lattice sites are called F-centres. These F-centres are responsible for the colour of the compound.

Question 24.
Aluminium crystallises in a cubic close-packed structure. Its metallic radius is 125 pm.

1. What is the length of the side of the unit cell?
2. How many unit cells are there in 1.00 cm³ of aluminium?

Answer:

1. For ccp structure, edge length, a = 2\(\sqrt{2}\)r = 2\(\sqrt{2}\) × 125 pm = 354 pm
2. Volume of unit cell = a³ = (354 × 10^-8)³ = 2.26 × 10²²

Question 25.
If NaCl is doped with 10^-3 mol % of SrCl₂, what is the concentration of cation vacancies?
Answer:
We know that doping of SrCl₂ to NaCl brings in the replacement of two Na⁺ ions by each Sr²⁺ ion, but each Sr²⁺ occupies only one lattice point. This produces one cation vacancy.
Thus, doping of 10^-3 mole of SrCl₂ in 100 moles of NaCI.
NaCI will produce cation vacancies = 10³ mol
∵ 100 mole of NaCI will have cation vacancies after doping = 10^-3 mol
∴ 1 mole of NaCI will have cation vacancies after doping = \(\frac{10^{-3}}{100}=10^{-5}\) mol
Total cationic vacancies after doping = 10^-5 × NA
= 10^-5 × 6.023 × 10²³
= 6.023 × 10¹⁸ vacancies.

Question 26.
Explain the following with suitable examples:

1. Ferromagnetism
2. Paramagnetism
3. Ferrimagnetism

1. Ferromagnetism is considered as an extreme case of paramagnetism. Those substances with a strong attraction to an external magnetic field and those retain a permanent magnetism even when the field is removed are known as ferromagnetic substances. Ferromagnetism is caused by the spontaneous alignment of magnetic moments of atoms or ions in the same direction. Examples of ferromagnetic substances are Fe, Co, Ni, CrO₂ alloys of Fe, Co and Ni, etc. Once such material is magnetised, it remains permanently magnetised.

2. Paramagnetic substances are substances which are attracted by the magnetic field and have unpaired electrons. They lose magnetism in the absence of magnetic field. The greater the number of unpaired electrons, the greater the magnetic moment of the substance and hence greater the paramagnetism, e.g. O2, CuO, Fe³⁺, Al, Mn, NO, Cu²⁺ etc.

3. These are substances which are expected to possess large magnetism on the basis of unpaired electrons but actually have small net magnetic moment. This is due to the alignment of magnetic moments in opposite directions in unequal numbers resulting in a net magnetic moment, e.g. Fe₃O₄, MgFe₂O₄.

4. These are substances which are expected to possess paramagnetism or ferromagnetism on the basis of unpaired electrons but actually they possess zero net magnetic moment. It arises due to the alignment of magnetic moments in opposite direction in a compensatory manner resulting a zero magnetic moment, e.g. MnO, MnO₂.

5. Germanium and silicon are group 14 elements and therefore, have a characteristic valence of four and form four bonds as in diamond. A large variety of solid-state materials have been prepared by a combination of groups 13 and 15 or 12 and 16 to simulate average valence of four as in Ge or Si.

Typical compounds of groups 13 – 15 are InSb, A1P and GaAs. Gallium arsenide (GaAs) semiconductors have a very fast response and have revolutionised the design of semiconductor devices. ZnS, CdS, CdSe, and HgTe are examples of groups 12 – 16 compounds. In these compounds, the bonds are not perfectly covalent and the ionic character depends on the electronegativities of the two elements.

GSEB Class 12 Chemistry The Solid State Additional Important Questions and Answers

Question 1.
(i) Find out the odd one from each group and justify your answer.
(a) NaCl, Iodine. Plastic, Ice
(b) Glass, Sugar, Rubber, Asphalt

(ii) From group (a) identify crystal (s).
(a) having a sharp melting point
(b) which is/are isotropic

(iii) What do you understand by isotropic properties?

(iv) List out any four points of differences between amorphous and crystalline solids?
Answer:
(i) Plastic – It is an amorphous solid while others are crystalline
Sugar – It is a crystalline solid while others are amorphous.

(ii) Since NaCl, iodine and ice are crystalline solids, have sharp melting points, ii. Since plastic is an amorphous solid, it is isotropic. The properties which have the same values in different directions are called isotropic properties.

(iii) The properties which have the same values in different directions are called isotropic properties.

(iv)

Crystalline solids	Amorphous solids
1. Possess long-range order.	1. Possess only short-range order.
2. Possess sharp melting points.	2. Do not possess a sharp melting point.
3. They are anisotropic, i.e., the physical properties such as electrical and thermal conductivity, refractive index, etc. are different in different directions.	3. They are isotropic, i.e., the physical properties are the same in all directions.
4. These can be cleaved along definite planes.	4. They undergo irregular cleavage on cutting.
5. More rigid.	5. Less rigid.

Question 2.
In a classroom seminar, Ramu explains the voids in crystal packing by suitably arranging lemon on the table.

1. What do you understand by the term void?
2. Using diagrams explain different types of voids?
3. If a small sphere is placed in the ‘void’ in each case, what would be the coordination number of the sphere? Explain.
4. What is the number of tetrahedral voids and octahedral voids in a crystal having ‘n’ particles?

Answer:

1. The vacant space in a crystal close-packed arrangement is known as void. There are two types of voids- tetrahedral and octahedral.
2. A void enclosed by four spheres is known as a tetrahedral void and a void surrounded by six spheres is known as an octahedral void.
   
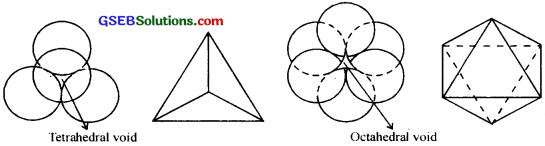
3. The coordination number of a sphere present in the tetrahedral void is 4 and that in the octahedral void is 6.
4. In a crystal having ‘n’ particles, the number of tetrahedral voids is ‘2n’ and the number of octahedral voids is ‘n’

Question 3.

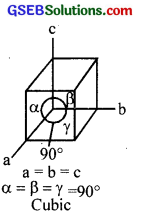
1. The dimensions of a crystal system determined is a = b = c, α = β = γ = 90°. Identify the crystal system and give the diagrammatic representation of it.
2. Explain the term ‘space lattice’ and ‘unit cell’.

Answer:
1. It is a cubical system.

2. The three-dimensional arrangement of constituent particles in a crystalline solid is called a space lattice and the smallest repeating unit in a space lattice is called a unit cell.

Question 4.
(a) The unit cell dimensions of a particular crystal system is given below.
a = b = c α = β = γ ≠ 90°
Identify the crystal system and suggest a suitable example.

(b) A certain metal M crystallises in fee lattice. It forms a compound with elements A and B. A occupies all the octahedral voids and B occupies half of the tetrahedral voids. Find out the empirical formula of the compound.
Answer:
(a) Rhombohedral. e.g. CaCO₃, HgS

(b) No. of M per unit cell = 4
No. of A per unit cell = 4
No. of B per unit cell = 1/2 × 8 = 4
Empirical formula = M₄A₄B₄ = MAB

Question 5.
(a) NaCl does not exhibit Frenkel defect. Do you agree? Justify.
(b) Assume that a fresh piece of KCl crystal is heated in an atmosphere of potassium vapours. Is there any colour change? Substantiate your answer.
Answer:
(a) Yes
The size of the two ions (Na⁺ and Cl^– is almost the same. So Na⁺ ions cannot be accommodated in the anionic interstitial site.

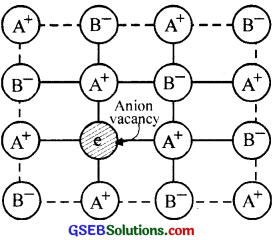
(b) Yes. Crystal develops violet colour due to the formation of F-centres.
When KCl crystals are heated in an atmosphere of potassium vapour, potassium is deposited on the surface of the KCl crystal and the chloride ions migrate from the bulk to the surface and combine with the potassium atom. The electron thus set free moves into the bulk of the crystal and F-centres are formed. The formation of F-centre imparts violet colour to the KCl crystal.

Question 6.
Name the parameters that characterize a unit cell.
Answer:
A unit cell is characterized by the following six parameters:

• The dimensions of the unit cell along the three edges. These are represented by a, b and c. The edges may or may not be mutually perpendicular.
• The angles between the edges. These are represented by α, β, and γ. The angle α  is. between b and c, β is between a and c and γ is between a and b.

Question 7.
(a) The following diagram shows the alignment of magnetic moments for some magnetic properties.

Which figure corresponds to antiferromagnetism? Justify your answer.
(b) Study the list of substances given below. Classify them on the basis of magnetic properties and name each class.
Al, TiO₂, Co, MnO₂, Benzene, O₂, NaCl, NH₃, Fe³⁺, Ni
Answer:
(a) Fig. (ii) Here the magnetic moments align in a compensatory way to give zero net magnetic moments.

(b)
(i) Diamagnetic substances – TiO₂, benzene, Nacl, NH₃
(ii) Paramagnetic substances – Al, O₂, Fe³⁺
(iii) Ferromagnetic substances – Co, Ni
(iv) Antiferromagnetic substances – MnO₂

Question 8.

1. A small number of K⁺ ions in KCl are substituted by Pr³⁺ ions. Draw the possible structure of the solid with a defect in the crystal lattice.
2. Semiconductors can be obtained by doping silicon with As or with Ga. What is the basic difference between these?

Answer:

1. 
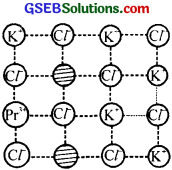
2. Doping Si with As gives n-type semiconductor
   Doping Si with Ga gives p-type semiconductor