Gujarat Board GSEB Textbook Solutions Class 12 Chemistry Chapter 4 Chemical Kinetics Textbook Questions and Answers, Additional Important Questions, Notes Pdf.
Gujarat Board Textbook Solutions Class 12 Chemistry Chapter 4 Chemical Kinetics
GSEB Class 12 Chemistry Chemical Kinetics InText Questions and Answers
Question 1.
For the reaction R → P, the concentration of a reactant changes from 0.03M to 0.02M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds?
Answer:
Rate = – \(\frac{∆[R]}{∆t}\) = – \(\frac{0.02-0.03M}{25min}\)
= 4 × 10-4 M min-1
Rate = – \(\frac{0.02-0.03M}{25×60s}\) = 6.7 × 10-4 M s-1
![]()
Question 2.
In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L-1 to 0.4 mol L-1 in 10 minutes. Calculate the rate during this interval?
Answer:
Rate = – \(\frac{1}{2}\) \(\frac{∆[A]}{∆t}\) = – \(\frac{1}{2}\) \(\frac { (0.4-0.5)molL^{ -1 } }{ 10min } \)
= 0.005 molL-1 min-1
Question 3.
For a reaction, A + B → Product; the rate law is given by, r = k [A]1/2 [B]2. What is the order of the reaction?
Answer:
Order of reaction = sum of powers of concentration of reactants.
Order of reaction = \(\frac { 1 }{ 2 } \) + 2 = \(\frac { 5 }{ 2 } \) = 2.5.
Question 4.
The conversion of molecules X to Y follows second-order kinetics. If the concentration of X is increased three times how will it affect the rate of formation of Y?
Answer:
Rate, r1 = k[X]2
If X increases by 3 times, then
rate, r2 = k[3X]2 = 9k[X]2 = 9r1
i.e., Rate is increased by 9 times.
![]()
Question 5.
A first-order reaction has a rate constant of 1.15 × 10-3s-1. How long will 5 g of this reactant take to reduce to 3 g?
Answer:
[A]0 = 5g, [A] = 3g, k = 1.15 × 10-3 s-1
t = \(\frac{2.303}{k}\) log \(\frac{[\mathrm{A}]_{0}}{[\mathrm{~A}]}\) = \(\frac{2.303}{1.15 \times 10^{-3} \mathrm{~s}^{-1}}\) log (\(\frac{5}{3}\)) = 444 s
Question 6.
The time required to decompose SO2Cl2 to half of its initial amount is 60 minutes. If the decomposition is a first-order reaction, calculate the rate constant of the reaction?
Answer:
t1/2 = 60 min. = 60 × 60 s
k = \(\frac{0.693}{t^{1 / 2}}\) = \(\frac{0.693}{60×60 sec}\) = 1.925 × 10-4S-1
Question 7.
What will be the effect of temperature on the rate constant?
Answer:
The rate of reaction increases with an increase in temperature and with 10°C rises in temperature its value becomes two times.
Arrhenius equation expresses the effect of temperature on constant
\(\mathrm{K}=\mathrm{A}_{e}^{-\mathrm{E}_{a} / \mathrm{RT}}\)
Where A is frequency factor and Efl is activation energy of the reaction.
![]()
Question 8.
The rate of the chemical reaction doubles for an increase of 10K in absolute temperature from 298K. Calculate Ea.
Answer:
K1 = k, k2 = 2k, T1 = 298K, T2 = 308 K, R = 8.314 JK-1mol-1
log \(\frac { k_{ 2 } }{ k_{ 1 } } \) = \(\frac{Ea}{2.303R}\) \(\left[\frac{\mathrm{T}_{2}-\mathrm{T}_{1}}{\mathrm{~T}_{1} \mathrm{~T}_{2}}\right]\)
log \(\frac{2k}{k}\) = \(\frac{Ea}{2.303×8.314}\) \(\frac{308-298}{308×298}\)
Ea = \(\frac{\log 2 \times 2.303 \times 8.314 \times 308 \times 298}{10}\) = 52898 Jmol-1 = 52.9 kJ mol-1
Question 9.
The activation energy for the reaction, 2HI(g) → H2 + I2(g) is 209.5 kJ mol-1 at 581 K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Answer:
Fraction of molecules having energy equal to or greater than activation energy,
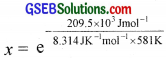
x = e-43.37
2.303 log x = – 43.37
log x = – \(\frac{43.37}{2.303}\) = -18.83
x = antilog (-18.83) = antilog (\(\bar{19}\).1700) = 1.46 × 10-19
GSEB Class 12 Chemistry Chemical Kinetics Text Book Questions and Answers
Question 1.
From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants?
- 3NO(g) → N2O(g) Rate = K[NO]2
- H2O2(aq) + 3I–(aq) + 2H+ → 2H2O(l) + I–3 Rate = k[H2O2] [I–]
- CH3CHO(g) → CH4(g) + CO(g) Rate = k[CH3CHO]3/2
- C2H5Cl(g) → C2H4(g) + HCl(g) Rate = k[C2H5Cl]
Answer:
- 2
- 2
- \(\frac{3}{2}\)
- 1
![]()
Question 2.
For the reaction 2A + B → A2B, the rate = k[A][B]2 with k = 2.0 × 10-6 mol-1L 2s-1. Calculate the initial rate of the reaction when [A] = 0.1 mol L-1, [B] = 0.2 mol L-1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L-1.
Answer:
Initial Rate = k[A][B]2 = 2 × 10-6 mol-1L2s-1 × (0.1 mol L-1) (0.2 mol L-1)2 = 8 × 10-9 mol L-1s-1
Rate of disappearance of B = \(\frac{1}{2}\) Rate of disappearance of A
When [A] is reduced by 0.1 – 0.06 = 0.04 M, [B] is reduce by \(\frac{1}{2}\) × 0.04
∴ [B] remaining = 0.2 – 0.02 = 0.18M
Rate of reaction = k[A][B]2
= 2 × 10-6 × 0.06 × (0.18)2 = 3.39 × 10-9 Ms-1
Question 3.
The decomposition of NH3 on platinum surface is zero order reaction. What are the rates of production of N2 and H2 if k = 2.5 × 10-4 mol-1L s-1?
Answer:
For zero-order reaction, rate of reaction = k

∴ Rate of production of N2 = k = 2.5 × 10-4 Ms-1
Rate of production of H2 = 3k
= 3 × 2.5 × 10-4 = 7.5 × 10-4 Ms-1
![]()
Question 4.
The decomposition of dimethyl ether leads to the formation of CH4, H2 and CO and the reaction rate is given by, Rate = k[CH3OCH3]3/2.
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e., Rate = \(\mathrm{k}\left(\mathrm{p}_{\mathrm{CH}, \mathrm{OCH}_{3}}\right)^{\frac{3}{2}}\).
If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?
Answer:
Unit of rate of reaction = bar min-1

Question 5.
Mention the factors that affect the rate of a chemical reaction?
Answer:
The rate of reaction depends upon the following factors:
- Concentration of reactants
- Temperature
- Catalyst
- Nature of reactant etc.
Question 6.
A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is
- doubled
- reduced to half?
Answer:
- Four times
- \(\frac{1}{4}\) times
![]()
Question 7.
What is the effect of temperature on the rate constant of a reaction? How can this temperature effect on rate constant be represented quantitatively?
Answer:
The rate of a reaction increases considerably with an increase in temperature. Rate constant of a reaction ¡s almost doubled for even 10° rise in temperature. The ratio between the rate constant of a reaction at two temperatures differing by 10° is called temperature coefficient of the reaction.
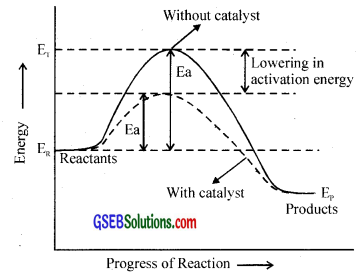
A quantitative relation between rate constant and temperature has been suggested by Arrhenius. It is called Arrhenius equation and is represented as k = A e-Ea/RT where the constant A is related to the number of binary molecular collisions per second per litre and is called the Arrhenius parameter (frequency factor). Ea is the activation energy, T is the temperature and R is the gas constant.
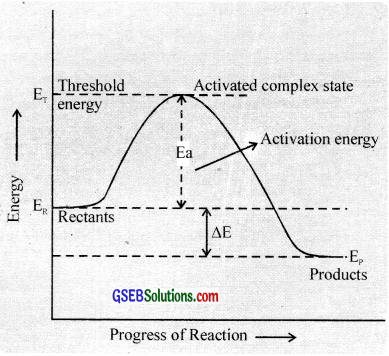
Transition state theory:
According to this theory, in a chemical reaction the reactant molecules must come together to form an activated complex. whose energy is higher than the reactant molecules before the activated complex is converted into product molecules. i.e., the reactant molecules have to acquire acerta amount of energy before they react to form the products.
This extra amount of energy is called activation energy. It is equal to the difference between the threshold energy needed for the reaction and the average kinetic energy of all the reacting molecules.
Activation energy = Threshold energy – Average kinetic energy of the reacting molecules.
In other words, there exists an energy barrier between the reactants and products. If the reactant molecules can cross this energy barrier by acquiring the actiation energy, they will be converted into products.
The concept of energy barrier may be further elaborated as follows.
Consider a hypothetical gaseous reaction.
A2 + B2 → 2AB
The reactant molecules react to form an intermediate called activated complex or transition state. In the formation of this complex. the bonds in the A2 and B2 molecules are loosened and new bonds between A and B are formed.
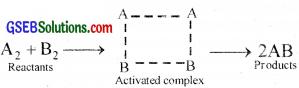
e.g. Reaction between H2 and I2
As the temperature increases, the number of molecules which can gain energy equal to or greater than energy of activation increases and hence more molecules can cross the energy barrier (can form activated complex) and rate of reaction increases.
k = Ae-Ea/RT
Taking logarithms lnA = lnA – \(\frac{Ea}{RT}\)
Converting to common logarithms, log k = log A – \(\frac{Ea}{2.303 RT}\)
Evaluation of Activation Energy:
Method (i):
The activation energy can be evaluated by the graphical method. This is done by plotting a graph between log k \(\frac{1}{T}\). The plot gives a straight line having a slope equal to \(\frac{-Ea}{2.303R}\).
Thus by knowing the value of slope and gas constant R, the activation energy, Ea can be calculated.
Ea – 2.303 R × slope
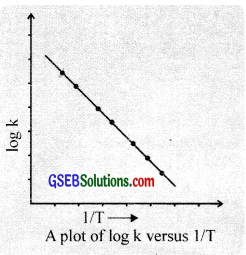
Method (ii):
Ea can be determined by measuring the values of rate constants at two different temperatures.
If k1 and k2 are the rate constants for the reaction at temperatures T1 and T2,
logk1 = log A – \(\frac{\mathrm{Ea}}{2.303 \mathrm{RT}_{1}}\) and …………….. (1)
logk2 = log A – \(\frac{\mathrm{Ea}}{2.303 \mathrm{RT}_{2}}\) and …………….. (2)
Subtrating cquatlon (1) from equation (2)
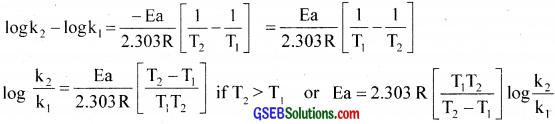
![]()
Question 8.
In pseudo-first-order hydrolysis of ester in water, the following results were obtained

- Calculate the average rate of reaction between the time interval of 30 to 60 seconds.
- Calculate the pseudo-first-order rate constant for the hydrolysis of the ester.
Answer:
Average rate = \(\frac{\text { Change in concentration }}{\text { Time interval }}\) = \(\frac{0.31-0.17}{60-30}\) = 4.67 × 10-3 Ms-1
For pseudo first order reaction,
Average rate = Rate constant × [Average concentration]

Question 9.
A reaction is first order in A and second order in B.
- Write the differential rate equation?
- How is the rate affected by increasing the concentration of B three times?
- How is the rate affected when the concentrations of both A and B are doubled?
Answer:
- Rate of reaction = \(\frac{-d[A]}{dt}\) = \(\frac{-\mathrm{d}[\mathrm{B}]^{2}}{\mathrm{dt}}\) = k[A] [B]2
- When the concentration of B is tripled, the rate of reaction increases by 9 times.
- Rate of reaction increases by 8 times.
Question 10.
In a reaction between A and B, the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:

What is the order of the reaction with respect to A and B?
Answer:
Let the rate law be, r = k[A]x[B]y
r1 = k[0.2]x[0.3]y = 5.07 × 10-5 …………………… (1)
r2 = k[0.2]x[0.1]y = 5.07 × 10-5 …………………… (2)
r3 = k[0.4]x[0.05]y = 7.6 × 10-5 …………………… (2)
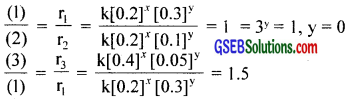
2x = 1.5
x = 0.585
![]()
Question 11.
The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D
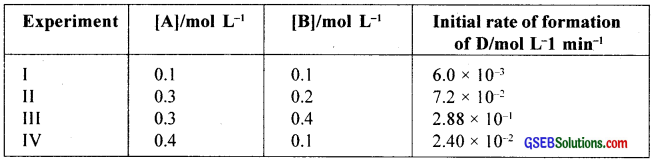
Determine the rate law and the rate constant for the reaction?
Answer:
Rate, r = k[A]x[B]y
r1 = k[0.1]x [0.1]y = 6.0 × 10-3 ………………….. (1)
r2 = k[0.3]x [0.2]y = 7.2 × 10-3 ………………….. (2)
r3 = k[0.3]x [0.4]y = 2.88 × 10-1 ………………….. (3)
r4 = k[0.4]x [0.1]y = 2.4 × 10-2 ………………….. (4)

Question 12.
The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:

Answer:
x = 0.2
y = 8 × 10-2
z = 1
Question 13.
Calculate the half-life of a first order reaction from their rate constants given below:
- 200 s-1
- 2min-1
- 4 years-1
Answer:
t1/2 = \(\frac{0.693}{k}\)
- t1/2 = \(\frac{0.693}{200 \mathrm{~s}^{-1}}\) = 3.465 × 10-3s
- t1/2 = \(\frac{0.693}{2 \mathrm{min}^{-1}}\) = 0.3465 min
- t1/2 = \(\frac{0.693}{4 \text { years }^{-1}}\) = 0.173 years
Question 14.
The half-life for the radioactive decay of 14HC is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample?
Answer:
[A]0 = 100
[A] = 80
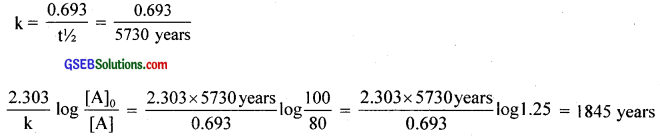
![]()
Question 15.
The rate constant for a first order reaction is 60 s-1. How much time will it take to reduce the intial concentration of the reactant to its \(\frac{1}{16}\)th value?
Answer:
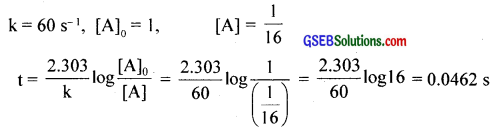
Question 16.
During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If µg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically?
Answer:
t1/2 = 2.81 years

Question 17.
For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 99% of reaction?
Answer:

Question 18.
A first order reaction takes 40 min for 30% decomposition. Calculate t1/2?
Answer:
[A]0 = 100
[A] = 100 – 30 = 70
t = 40 min

Question 19.
The rate constant for the decomposition of hydrocarbons is 2.148 × 10-5s-1 at 546 K. If the energy of activation is 179.9 KJ/mol, what will be the value of the pre-exponential factor?
Answer:
k = 2.418 × 10-5s-1
T = 546 K
Ea = 179.9 × 10-3 J mol-1
k = Ae-Ea/RT
log k = log A – \(\frac{Ea}{2.303RT}\)
log A = log k + \(\frac{Ea}{2.303RT}\) = log (2.418 × 10-5) + \(\frac{179.9 \times 10^{3}}{2.303 \times 8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1} \times 546 \mathrm{~K}}\)
On solving, A = 3.912 × 1012S-1
![]()
Question 20.
Consider a certain reaction A → Products with k = 2.0 × 10-2s-1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L-1?
Answer:
[A]0 = 1 molL-1, t = 100 s, k = 2.0 × 10-2s-1
k = \(\frac{2.303}{t}\) log \(\frac{[\mathrm{A}]_{0}}{[\mathrm{~A}]}\)
2.0 × 10-2S-1 = \(\frac{2.303}{100s}\) log \(\frac{1 \mathrm{~mol} \mathrm{~L}^{-1}}{[\mathrm{~A}]}\)
log [A] = -0.8684
[A] = antilog (-0.8684) = antilog (\(\bar{1}\).1316) = 0.1354 molL-1
Question 21.
Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t1/2 = 3.00 hours. What fraction of sample of sucrose remains after 8 hours?
Answer:
t1/2 = 3hrs

Question 22.
The decomposition of hydrocarbon follows the equation k = (4.5 × 1011 s-1)\(e^{\frac{-28000 K}{T}}\) Calculate Ea?
Answer:
According to Arrehenius equation, k = \(\mathrm{Ae}^{\frac{-\mathrm{Ea}}{\mathrm{RT}}}\) …………………… (1)
Given, k = (4.5 × 10-11s-1)\(\mathrm{e}^{\frac{-28000 \mathrm{~K}}{\mathrm{~T}}}\) ………………….. (2)
On comparing the equations, \(\frac{-Ea}{RT}\) = \(\frac{-28000K}{T}\)
Ea = 28000 KR = 28000 K × 8.314 JK-1 mol-1 = 232.79 kJ mol-1
Question 23.
The rate constant for the first order of decomposition of H2O2 is given by the following equation:
log k = 14.34 – \(\frac{1.25 \times 10^{4} \mathrm{~K}}{\mathrm{~T}}\)
log k = log A – \(\frac{Ea}{2.303RT}\)
Given log k = 14.34 – \(\frac{1.25 \times 10^{4} \mathrm{~K}}{\mathrm{~T}}\)
Comparing the equations, \(\frac{Ea}{2.303RT}\) = \(\frac{1.25 \times 10^{4} \mathrm{~K}}{\mathrm{~T}}\)
Ea = 2.303 × R × 1.25 × 104K = 2.303 × (8.314 JK-1 mol-1) × 1.25 × 104K = 239.34 KJ mol-1
When t1/2 = 256 min, k = \(\frac{0.693}{t^{1 / 2}}\) = \(\frac{0.693}{256×60s}\) = 4.51 × 10-5 s-1?
Substituting the value in the given equation and solving, T = 669 K
Question 24.
The decomposition of A into product has value of k as 4.5 × 103s-1, k2 = 1.5 × 104s-1, T1 = 283 K, T2 = ?
Ea = 60 × 103 J mol-1
R = 8.314 JK-1mol-1

On solving, T2 = 24°C
![]()
Question 25.
The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature?
Answer:
T1 = 293 K, k1 = k, T2 = 313 K, k2 = 4k
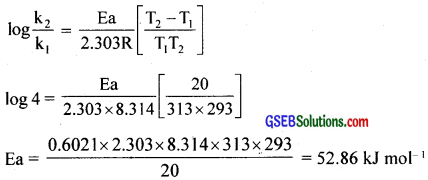
GSEB Class 12 Chemistry Chemical Kinetics Additional Important Questions and Answers
Question 1.
- Define the order of a reaction?
- How does order differ from the molecularity of a reaction?
- The following reactions follow first-order kinetics. Write the rate law of these reactions?
(a) 2N2O5(g) → 4NO2(g) + O2(g)
(b) NH4NO2 → N2 + 2H2O
(c)
![]()
Answer:
1. The order of a reaction is defined as the sum of the powers to which the concentration terms are raised in the rate law.
For a general reaction, aA + bB → cC + dD,
rate = k[A]x[B]y
∴ Order of the reaction = x + y
2. Molecularity of a reaction is the total number of molecules or atoms or ions that collide simultaneously to bring about the reaction.
Thus the molecularity of the above reaction is a + b.
3.
- Rate = k [N2O5]
- Rate = k [NH4NO2]
- Rate = k [CH3COOC2H5]
![]()
Question 2.
Hydrogen reacts with halogen to form hydrogen halides. Write the rate law and find the order of the following reactions?

- H2 + Br2 → 2HBr
- H2 + I2 → 2HI
Answer:
1.
![]()
Rate = k[H2]0[Cl2]0, Zero order reaction
2. H2 + Br2 → 2HBr
3. H2 + I2 → 2HI
Rate = k[H2][I2], order = 2
Question 3.
- Define the order of a reaction.
- Derive the integrated rate equation for a first order reaction.
- The halfe life of a first order reaction is 20 minutes. Calculate the rate constant of the reaction.
Answer:
1. The order of a reaction is defined as the sum of the powers to which the concentration terms are raised in the rate law.
For a general reaction
aA + bB → cC + dD,
rate = k[A]x[B]y
∴ Order of the reaction = x + y
2. If the rate of a reaction depends only on the first power of the concentration of one of the reactants, it is said to be a first order reaction.
For a first order reaction,
For a first order reaction depends only on the first power of the concentration of one of the reactants, it is said to be a first order reaction.
For a first order reaction, A → Products, if [A] is the concentration of the reactant A, and k is the rate constant, rate = k[A] ……………… (1) and rate = \(\frac{-d[A]}{dt}\) …………………… (2)
Equating (1) & (2) we get, \(\frac{-d[A]}{dt}\) = k[A] …………………. (3)
This is the differential form of rate law.
Rearranging equation (3), \(\frac{-d[A]}{[A]}\) = k.dt
Integrating the two sides, we get
-ln[A] = kt + C ………………… (4)
Where C is a constant and is determined from an initial conditions.
When t = 0, [A] = [A]0, ∴ -ln[A]0 = k(0) + C (or) C = -ln [A]0 ……………………. (5)
Substituting (5) in (4) we get, ln [A] = kt – ln[A]0
ln[A]0 – ln[A] = kt
ln \(\frac{[\mathrm{A}]_{0}}{[\mathrm{~A}]}\) = kt
kt = 2.303 log \(\frac{[\mathrm{A}]_{0}}{[\mathrm{~A}]}\) ……………………. (6)
Equation (6) is called integrated rate expression for the first order reaction.
3. t1/2 = 20 mins
k = ?
But k = \(\frac{0.693}{t^{1 / 2}}\) = \(\frac{0.693}{20}\) = 3.465 × 10-2 min-1
![]()
Question 4.
In a classroom discussion about order and molecularity of a chemical reaction, Arjun argues that, “there are reactions which appear to be of higher order but actually follow lower order kinetics”. How far is this argument true? What is your opinion in this regard? Justify your answer using suitable examples.
Answer:
Arjun’s argument is correct. There are reactions which appear to be of higher order but actually follow lower order kinetics. Reactions which appear to be of higher order but actually follow lower order kinetics are called pseudo-order reactions, e.g. Hydrolysis of ethyl acetate

Rate, r = k[CH3COOC2H5]
The concentration of H2O is very high and it does not change appreciably and does not appear in the rate law.
Question 6.
The rate law for a reaction is found to be
Rate = K [NO–2] [I– ] [H+]2 How would the rate of reaction change when
(i) Concentration of H+ is doubled
(ii) Concentration of I– is halved
(iii) Concentration of each of NO2, I– and H+ are tripled?
Answer:
Suppose initially the concentration are [NO–2] = a mol L-1, [I– ] = b mol L– and [H+] = c mol L-1
∴ Rate = K abc2
(i) New [H+] = 2c
∴ New rate = 4ab (2c)2 = 4abc2
= 4 times
(ii) New [I– ] = \(\frac { b }{ 2 }\)
New Rate = Ka\(\frac { b }{ 2 }\)c2= \(\frac { 1 }{ 2 }\) Kabc2
ie. rate of reaction is halved
(iii) New [NO–2] = 3a, [I– ] = 3b, [H+] = 3c
New rate = K (3a) (3b) (3c)2 = 81K abc2 = 81 times.
![]()
Question 6.
Rate constant K of a reaction varies with temperature according to the equation
log K = constant . \(\frac{\mathbf{E} \mathbf{a}}{2.303 \mathbf{R}} \frac{\mathbf{1}}{\mathbf{T}}\)
Answer:
where Ea is the energy of activation for the reaction. When a graph is plotted for
log K versus\(\frac { 1 }{ T }\), a straight line with a slope 6670 K is obtained. Calculate the energy of activation for this reaction. State units (R = 8.314JK-1 mol-1)
Answer:
Slope of the lin,e
\(\frac{-E a}{2.303 R}\) =-6670K
Ea = 2.303 × 8.314 (JK-1 mol-1) × 6670K = 127711.4J mol-1.
Question 7.
Read the following statement.
“Activation energies are low for fast reactions and high for slow reactions”.
a. Justify the statement.
b. The rate of a reaction quadruples when the temperature changes from 310K to 330K. Calculate the activation energy of the reaction.
(R = 8.314 JK-1mol-1)
Answer:
a. If activation energy Ea is low, large number of molecules can have this energy. So number of effective collision will be large. So such reactions have high speed. If the activation energy is high, less number of molecules have the activation energy, so reaction rate will be low.
b.

![]()
Question 8.
Study the following reaction.
2SO2(g) + O2(g) ⇄ 2SO3(g); ∆H = -196.6KJ
Here to get more yield of SO3, a catalyst is used.
Answer:
This reaction is an exothermic reaction. For exothermic reaction Ep < ER.
Question 9.
- Explain why the values of order and molecularity are different for the following reaction.

- List out the important points of differences between order and molecularity?
Answer:
1. This is an example of a pseudo order reaction. The molecularity of the reaction is 2 while order is 1.
Reactions which appear to be of higher order but actually follow lower order kinetics are called pseudo-order reactions, e.g. Hydrolysis of ethyl acetate.
![]()
Rate r = k[CH3COOC2H5]
Concentration of H2O is very high and it does not change appreciably and does not appear in the rate law.
2.
|
Order |
Molecularity |
| 1. It is sum of the powers of the concentration terms in the rate law expression | It is the number of reacting species undergoing simultaneous collision in the reaction. |
| 2. It is determined experimentally. | It is a theoretical concept. |
| 3. It can be a whole number, fraction or even zero. | It is always a whole number. |
| 4. It gives some idea about reaction mechanism. | It doesn’t tell us anything about the mechanism of the reaction. |