Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 10 Vector Algebra Ex 10.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 10 Vector Algebra Ex 10.2
Question 1.
Compute the magnitudes of the following vectors:
\(\vec{a}\) = \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \),
\(\vec{b}\) = 2\(\hat {i} \) – 7\(\hat {j} \) – 3\(\hat {k} \),
\(\vec{c}\) = \(\frac{1}{\sqrt{3}}\)\(\hat {i} \) + \(\frac{1}{\sqrt{3}}\)\(\hat {j} \) – \(\frac{1}{\sqrt{3}}\)\(\hat {k} \)
Solution:

![]()
Question 2.
Write two different vectors having the same magnitude.
Solution:
Consider the vectors \(\vec{a}\) = \(\hat {i} \) + 2\(\hat {j} \) + \(\hat {k} \) and \(\vec{b}\) = \(\hat {i} \) + \(\hat {j} \) + 2\(\hat {k} \).
|\(\vec{a}\)| = \(\sqrt{1^{2}+2^{2}+1^{2}}\) = \(\sqrt{6}\), |\(\vec{b}\)| = \(\sqrt{1^{2}+1^{2}+2^{2}}\) = \(\sqrt{6}\)
Thus, two different vectors \(\vec{a}\) and \(\vec{b}\) have the same magnitude.
Question 3.
Write two different vectors having same direction.
Solution:
Let the two vectors be
\(\vec{a}\) = \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \)
\(\vec{b}\) = 3\(\hat {i} \) + 3\(\hat {j} \) + 3\(\hat {k} \)
Direction cosines of \(\vec{a}\) are
(\(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\),\(\frac{1}{\sqrt{3}}\)) and direction cosines of \(\vec{b}\)
are (\(\frac{3}{\sqrt{27}}\), \(\frac{3}{\sqrt{27}}\), \(\frac{3}{\sqrt{27}}\)), i.e; (\(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\)).
Hence, vectors \(\vec{a}\) and \(\vec{b}\) have the same direction but different magnitude.
Question 4.
Find the values of x and y so that the vectors 2\(\hat {i} \) + 3\(\hat {j} \) and x\(\hat {i} \) + y\(\hat {j} \) are equal.
Solution:
2\(\hat {i} \) + 3\(\hat {j} \) = x\(\hat {i} \) + y\(\hat {j} \)
Equation the coefficients of \(\hat {i} \) and \(\hat {j} \), we get
x = 2, y = 3.
![]()
Question 5.
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (- 5, 7).
Solution:
Let A(2, 1) be the initial point and B(- 5, 7) be the terminal point.
∴ \(\overrightarrow{\mathrm{AB}}\) = (x2 – x1)\(\hat {i} \) + (y2 – y1)\(\hat {j} \)
= (- 5 – 2)\(\hat {i} \) + (7 – 1)\(\hat {j} \) = – 7\(\hat {i} \) + 6\(\hat {j} \).
∴ The vector components are – 7\(\hat {i} \) and 6\(\hat {j} \) and scalar components are – 7 and 6.
Question 6.
Find the sum of the vectors \(\vec{a}\) = \(\hat {i} \) – 2\(\hat {j} \) + \(\hat {k} \), \(\vec{b}\) = – 2\(\hat {i} \) + 4\(\hat {j} \) + 5\(\hat {k} \) and \(\vec{c}\) = \(\hat {i} \) – 6\(\hat {j} \) – 7\(\hat {k} \).
Solution:
Sum of vectors = \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\)
= (\(\hat {i} \) – 2\(\hat {j} \) + \(\hat {k} \)) + (- 2\(\hat {i} \) + 4\(\hat {j} \) + 5\(\hat {k} \)) + (\(\hat {i} \) – 6\(\hat {j} \) – 7\(\hat {k} \))
= (\(\hat {i} \) – 2\(\hat {i} \) + \(\hat {i} \)) + (- 2\(\hat {j} \) + 4\(\hat {j} \) – 6\(\hat {j} \)) + (\(\hat {k} \) + 5\(\hat {k} \) – 7\(\hat {k} \))
= 0\(\hat {i} \) – 4\(\hat {j} \) – \(\hat {k} \) = – 4\(\hat {j} \) – \(\hat {k} \).
![]()
Question 7.
Find the unit vector in the direction of the vector \(\vec{a}\) = \(\hat {i} \) + \(\hat {j} \) + 2\(\hat {k} \).
Solution:
\(\vec{a}\) = \(\hat {i} \) + \(\hat {j} \) + 2\(\hat {k} \)
∴ |\(\vec{a}\)| = \(\sqrt{1^{2}+1^{2}+2^{2}}\) = \(\sqrt{6}\).
∴ Unit vector in the direction of vector \(\vec{a}\)
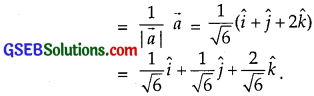
Question 8.
Find the unit vector in the direction of vector \(\overrightarrow{\mathrm{PQ}}\), where P and Q are the points (1, 2, 3) and (4, 5, 6) respectively.
Solution:
The points P and Q are (1, 2, 3) and (4, 5, 6) respectively.
∴ The vector \(\overrightarrow{\mathrm{PQ}}\) = (x2 – x1)\(\hat {i} \) + (y2 – y1)\(\hat {j} \) + (z2 – z1)\(\hat {k} \)
∴ \(\overrightarrow{\mathrm{PQ}}\) = (4 – 1)\(\hat {i} \) + (5 – 2)\(\hat {j} \) + (6 – 3)\(\hat {k} \)
= 3\(\hat {i} \) + 3\(\hat {j} \) + 3\(\hat {k} \)
∴ |\(\overrightarrow{\mathrm{PQ}}\)| = \(\sqrt{3^{2}+3^{2}+3^{2}}\) = \(\sqrt{27}\) = 3\(\sqrt{3}\).
∴ Unit vector in the direction of
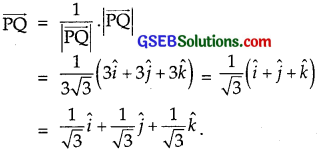
![]()
Question 9.
For given vectors \(\vec{a}\) = 2\(\hat {i} \) – \(\hat {j} \) + 2\(\hat {k} \) and \(\vec{b}\) = – \(\hat {i} \) + \(\hat {j} \) – \(\hat {k} \), find the unit vector in the direction of the vector \(\vec{a}\) + \(\vec{b}\).
Solution:
\(\vec{a}\) = 2\(\hat {i} \) – \(\hat {j} \) + 2\(\hat {k} \) and \(\vec{b}\) = – \(\hat {i} \) + \(\hat {j} \) – \(\hat {k} \)
∴ \(\vec{a}\) + \(\vec{b}\) = (2\(\hat {i} \) – \(\hat {j} \) + 2\(\hat {k} \)) + (-\(\hat {i} \) + \(\hat {j} \) – \(\hat {k} \))
= (2 – 1)\(\hat {i} \) + (-1 + 1)\(\hat {j} \) + (2 – 1)\(\hat {k} \)
= \(\hat {i} \) + 0.\(\hat {j} \) + \(\hat {k} \) = \(\hat {i} \) + \(\hat {k} \)
So, |\(\vec{a}\) + \(\vec{b}\)| = \(\sqrt{1^{2}+1^{2}}\) = \(\sqrt{2}\).
∴ Unit vector in the direction of \(\vec{a}\) + \(\vec{b}\)
= \(\frac{1}{|\vec{a}+\vec{b}|}\)(\(\vec{a}\) + \(\vec{b}\)) = \(\frac{1}{\sqrt{2}}\)(\(\hat {i} \) + \(\hat {k} \)) = \(\frac{1}{\sqrt{2}}\)\(\hat {i} \) + \(\frac{1}{\sqrt{2}}\)\(\hat {k} \)
Question 10.
Find a vector in the direction of 5\(\hat {i} \) – \(\hat {j} \) + 2\(\hat {k} \) which has magnitude 8 units.
Solution:
The given vector is
\(\vec{a}\) = 5\(\hat {i} \) – \(\hat {j} \) + 2\(\hat {k} \).
∴ |\(\vec{a}\)| = \(\sqrt{5^{2}+(-1)^{2}+2^{2}}\) = \(\sqrt{25+1+4}\) = \(\sqrt{30}\).
∴ Unit vector in the direction of vector \(\vec{a}\)
= \(\frac{1}{\sqrt{30}}\)(5\(\hat {i} \) – \(\hat {j} \) + 2\(\hat {k} \).
∴Vector of magnitude 8 in the direction of vector \(\vec{a}\)
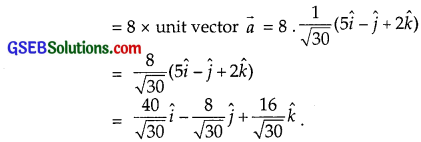
![]()
Question 11.
Show that the vectors 2\(\hat {i} \) – 3\(\hat {j} \) + 4\(\hat {k} \) and – 4\(\hat {i} \) + 6\(\hat {j} \) – 8\(\hat {k} \) are collinear.
Solution:
\(\vec{a}\) = – 2\(\hat {i} \) – 3\(\hat {j} \) + 4\(\hat {k} \)
\(\vec{b}\) = – 4\(\hat {i} \) + 6\(\hat {j} \) – 8\(\hat {k} \) = – 2(2\(\hat {i} \) – 3\(\hat {j} \) + 4\(\hat {k} \))
Vectors \(\vec{a}\) and \(\vec{b}\) have the same direction. Therefore, they are collinear.
Question 12.
Find the direction cosines of the vectors \(\hat {i} \) + 2\(\hat {j} \) + 3\(\hat {k} \).
Solution:
Directions cosines of vector x\(\hat {i} \) + y\(\hat {j} \) + z\(\hat {k} \) are

Here, for the vector \(\vec{a}\) = \(\hat {i} \) + 2\(\hat {j} \) + 3\(\hat {k} \)
x = 1, y = 2, z = 3
∴ \(\sqrt{x^{2}+y^{2}+z^{2}}\) = \(\sqrt{1^{2}+2^{2}+3^{2}}\) = \(\sqrt{1+4+9}\) = \(\sqrt{14}\).
∴ Direction of cosines are given by

![]()
Question 13.
Find the direction cosines of the vector joining the points A(1, 2, – 3) and B(- 1, – 2, 1), directed from A to B.
Solution:
Vector joining the points A and B is
(x2 – x1)\(\hat {i} \) + (y2 – y1)\(\hat {j} \) + (z2 – z1)\(\hat {k} \)
Here, A is (1, 2, – 3)
∴ x1 = 1, y1 = 2, z1 = – 3.
B is (- 1, – 2, 1)
∴ x2 = – 1, y2 = – 2, z2 = 1.
∴ Vector joining the points A and B
= \(\overrightarrow{\mathrm{AB}}\) = (- 1 – 1)\(\hat {i} \) + (- 2 – 2)\(\hat {j} \) + [1 – (- 3)]\(\hat {k} \)
= – 2\(\hat {i} \) – 4\(\hat {j} \) + 4\(\hat {k} \).
Direction cosines of vectors x\(\hat {i} \) + y\(\hat {j} \) + z\(\hat {k} \) are

Question 14.
Show that the vector \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \) is equally inclined to the axes OX, OY and OZ.
Solution:
Let \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \) = a.
Direction cosines of vector x\(\hat {i} \) + y\(\hat {j} \) + z\(\hat {k} \) are

which shows that the vector \(\vec{a}\) is equally inclined to the axes OX, OY and OZ.
![]()
Question 15.
Find the position vector of a point R which divides the line segment joining the points, whose positive vectors are
P (\(\hat {i} \) + 2\(\hat {j} \) – \(\hat {k} \)) and Q(- \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \)), in the ratio 2 : 1
(i) internally,
(ii) externally.
Solution:
(i) Internal Division:
The point R which divides the line segment joining the points P(\(\vec{a}\)) and Q(\(\vec{b}\)) in the ratio m : n is given by

(ii) External Division:
Similarly, the point R’ which divides PQ externally in the ratio m : n is given by
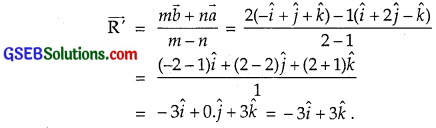
Question 16.
Find the mid-point of the vector joining the points P(2, 3, 4) and Q(4, 1, – 2).
Solution:
Mid point of the vector joining the points P(\(\vec{a}\)) and Q(\(\vec{b}\)) is \(\frac{\vec{a}+\vec{b}}{2}\).
Here, \(\vec{a}\) = 2\(\hat {i} \) + 3\(\hat {j} \) + 4\(\hat {k} \) and \(\vec{b}\) = 4\(\hat {i} \) + \(\hat {j} \) – 2\(\hat {k} \).
∴ Required mid-point is
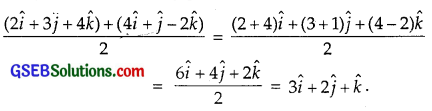
![]()
Question 17.
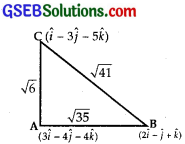
Show that the points A, B and C with position vectors \(\vec{a}\) = 3\(\hat {i} \) – 4\(\hat {j} \) – 4\(\hat {k} \),
\(\vec{b}\) = 2\(\hat {i} \) – \(\hat {j} \) + \(\hat {k} \) and \(\vec{c}\) = \(\hat {i} \) – 3\(\hat {j} \) – 5\(\hat {k} \), respectively form the vertices of a right angled traiangle.
Solution:
\(\overrightarrow{\mathrm{AB}}\) = \(\vec{b}\) – \(\vec{a}\)
= (2\(\hat {i} \) – \(\hat {j} \) + \(\hat {k} \)) – (3\(\hat {i} \) – 4\(\hat {j} \) – 4\(\hat {k} \))
= – \(\hat {i} \) + 3\(\hat {j} \) + 5\(\hat {k} \).
So, |\(\overrightarrow{\mathrm{AB}}\)| = (- 1)2 + 32 + 52
= 1 + 9 + 25 = 35
\(\overrightarrow{\mathrm{BC}}\) = \(\vec{c}\) – \(\vec{b}\)
= (\(\hat {i} \) – 3\(\hat {j} \) – 5\(\hat {k} \)) – (2\(\hat {i} \) – \(\hat {j} \) + \(\hat {k} \))
= (1 – 2)\(\hat {i} \) + (- 3 + 1)\(\hat {j} \) + (- 5 – 1)\(\hat {k} \) = – \(\hat {i} \) – 2\(\hat {j} \) – 6\(\hat {k} \).
∴ |\(\overrightarrow{\mathrm{BC}}\)|2 = (- 1)2 + (- 2)2 + (- 6)2 = 1 + 4 + 36 = 41.
\(\overrightarrow{\mathrm{CA}}\) = \(\vec{a}\) – \(\vec{c}\) = (3\(\hat {i} \) – 4\(\hat {j} \) – 4\(\hat {k} \)) – (\(\hat {i} \) – 3\(\hat {j} \) – 5\(\hat {k} \))
= (3 – 1)\(\hat {i} \) + (- 4 + 3)\(\hat {j} \) + (- 4 + 5)\(\hat {k} \) = 2\(\hat {i} \) – \(\hat {j} \) + \(\hat {k} \).
|\(\overrightarrow{\mathrm{CA}}\)|2 = 22 + (- 1)2 = 4 + 1 + 1 = 6.
Now, |\(\overrightarrow{\mathrm{AB}}\)|2 + |\(\overrightarrow{\mathrm{AC}}\)|2 = 35 + 6 = 41 = |\(\overrightarrow{\mathrm{BC}}\)|2
or |\(\overrightarrow{\mathrm{AB}}\)|2 + |\(\overrightarrow{\mathrm{AC}}\)|2 = |\(\overrightarrow{\mathrm{BC}}\)|2
Hence, ∆ ABC is a right angled traiangle, right angled at A.
![]()
Question 18.
In triangle ABC, which of the following is not true?
(A) \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) + \(\overrightarrow{\mathrm{CA}}\) = \(\vec{0}\)
(B) \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) – \(\overrightarrow{\mathrm{AC}}\) = \(\vec{0}\)
(C) \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) – \(\overrightarrow{\mathrm{CA}}\) = \(\vec{0}\)
(D) \(\overrightarrow{\mathrm{AB}}\) – \(\overrightarrow{\mathrm{CB}}\) + \(\overrightarrow{\mathrm{CA}}\) = \(\vec{0}\)
Solution:
By traingle law of vector addition,
\(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) = \(\overrightarrow{\mathrm{AC}}\) or \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) = – \(\overrightarrow{\mathrm{CA}}\)
or \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) + \(\overrightarrow{\mathrm{CA}}\) = \(\vec{0}\)
Thus, part (C) \(\overrightarrow{\mathrm{AB}}\) + \(\overrightarrow{\mathrm{BC}}\) – \(\overrightarrow{\mathrm{CA}}\) = \(\vec{0}\) is not true.
![]()
Question 19.
If \(\vec{a}\) and \(\vec{b}\) are two collinear vectors, then which of the following is incorrect:
(A) \(\vec{b}\) = λ\(\vec{a}\), for some scalar
(B) \(\vec{a}\) = ± \(\vec{b}\)
(C) the respective components of \(\vec{a}\) and \(\vec{b}\) are proportional.
(D) both the vectors \(\vec{a}\) and \(\vec{b}\) have same direction, but different magnitude.
Solution:
Part (D) is incorrect since both the vectors \(\vec{a}\) and \(\vec{b}\), being collinear, are not necessarily in the same direction.
They may have opposite directions. Their magnitudes may be different.