Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 9 Differential Equations Ex 9.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 9 Differential Equations Ex 9.5
In each of the questions 1 to 10, show that the given differential equation is homogeneous and solve each of them:
Question 1.
(x2 + x dy) = (x2 + y2) dx
Solution:
(x2 + xy) dy = (x2 + y2)dx
or \(\frac{dy}{dx}\) = \(\frac{x^{2}+y^{2}}{x^{2}+x y}\) = f(x, y) (say) …………….. (1)
where f(x, y) = \(\frac{x^{2}+y^{2}}{x^{2}+x y}\)
Replacing by λx and y by λy, we get
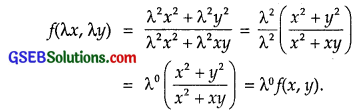
Hence, f(x, y) is a homogeneous function of degree zer0.
To solve it, put y = vx or
\(\frac{dy}{dx}\) = v + x \(\frac{dv}{dx}\)
Equation (1) may be written as
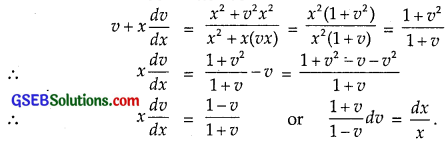
Integrating, we get
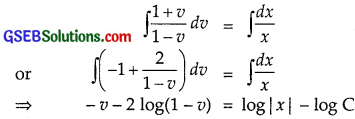
Put v = \(\frac{y}{x}\), we get

∴ Solution is (x – y)2 = Cxe-y/x.
![]()
Question 2.
y’ = \(\frac{x+y}{x}\)
Solution:
y’ = \(\frac{x+y}{x}\)
∴ \(\frac{dy}{dx}\) = f(x, y), where f(x, y) = \(\frac{x+y}{x}\).
Replacing x by λx and y by λy,
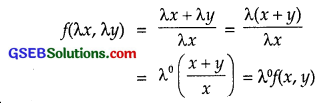
∴ f(x, y) is a homogeneous function of degree zero.

Putting v = \(\frac{y}{x}\), we get \(\frac{y}{x}\) = log |x| + C or y = x log |x| + Cx.
Question 3.
(x – y)dy – (x + y)dx = 0
Solution:
(x – y) dy – (x + y)dx = 0
or \(\frac{dy}{dx}\) = \(\frac{x+y}{x-y}\) = f(x, y)
∴ f(x, y) = \(\frac{x+y}{x-y}\)
Replacing x by λx and y by λy,
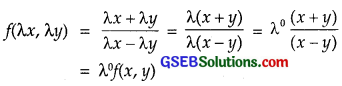
⇒ f(x, y) is a homogeneous function of degree zero.
Put y = vx so that

Integrating, we get

![]()
Question 4.
(x2 – y2)dx + 2xy dy = 0
Solution:
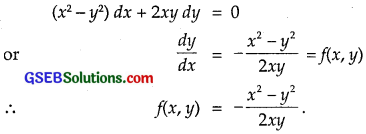
Replacing x by λx and y by λy, we get
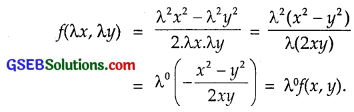
Hence, f(x, y) is a homogeneous functoin of degree zero.

Integrating, we get
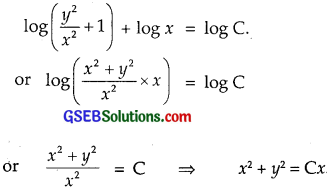
Question 5.
x2 \(\frac{dy}{dx}\) = x2 – 2y2 + xy
Solution:

Replacing x by λx and y by λy in f(x, y), we get

∴ f(x, y) is a homogenous function of degree zero.
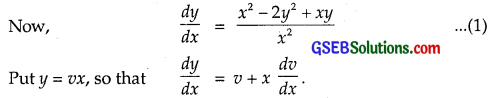
Putting these values in (1), we get
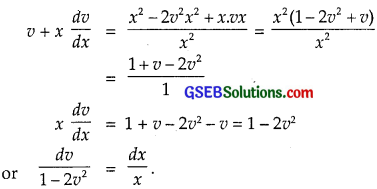
Integrating, we have:

Put \(\sqrt{2}\)v = t so that \(\sqrt{2}\)dv = dt.

Put v = \(\frac{y}{x}\), we get the solution as

![]()
Question 6.
x dy – y dx = \(\sqrt{x^{2}+y^{2}}\) dx
Solution:
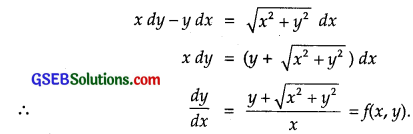
Replacing x by λx and y by λy in f(x, y), we get

∴ f(x, y) is a homogenous function of degree zero.

Putting these values in (1), we get

Integrating, we have:

Question 7.
{x cos (\(\frac{y}{x}\)) + y sin (\(\frac{y}{x}\))} y dx = {y sin (\(\frac{y}{x}\)) – x cos (\(\frac{y}{x}\))} x dy
Solution:
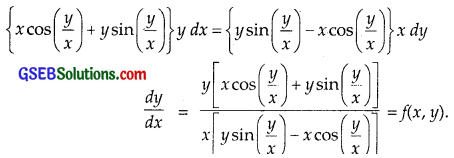
Replacing x by λx and y by λy in f(x, y), we get

∴ f(x, y) is a homogenous function of degree zero.
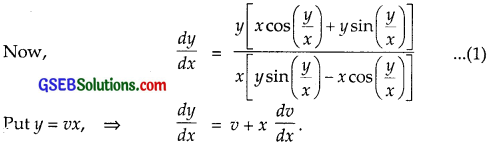
Putting in these values in (1), we get

Transposing v to R.H.S., we get

Integrating, we get

![]()
Question 8.
x \(\frac{dy}{dx}\) – y + x sin \(\frac{y}{x}\) = 0
Solution:
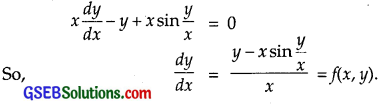
Replacing x by λx and y by λy in f(x, y), we get

∴ f(x, y) is a homogenous function of degree zero.

Question 9.
y dx + xlog (\(\frac{y}{x}\))dy – 2x dy = 0
Solution:

Replacing x by λx and y by λy in f(x, y), we get

Put y = vx, so that
\(\frac{dy}{dx}\) = v + x \(\frac{dv}{dx}\).
Putting these values in (2), we get
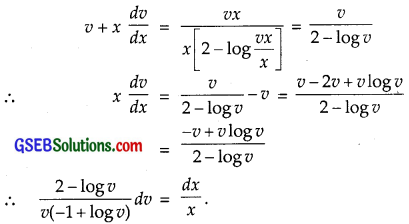
Integrating, we get
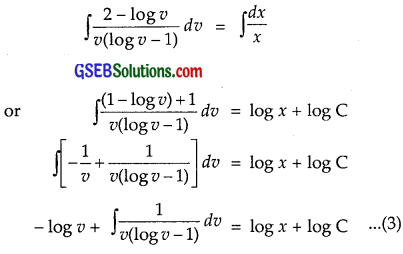
Put log v – 1 = t, so that \(\frac{1}{v}\)dv = dt
Therefore, from (3), we get
– log v + ∫ \(\frac{dt}{t}\) = log x + log C
⇒ – log v + log t = log x + log C
or – log v + log (log v – 1) = log x + log C
or log (log v – 1) = log v + log x + log C
= log v Cx
Put v = \(\frac{y}{x}\). Then the solution is

![]()
Question 10.
(1 + ex/y)dx + ex/y(1 – \(\frac{x}{y}\))dy = 0
Solution:

Replacing x by λx and y by λy and obtain:
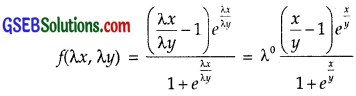
Hence, f(x, y) is a homogeneous function of degree zero.

Integrating, we get

∴ Required solution is x + y ex/y = Cy.
For each of the differential equations in questions 11 to 15, find the particular solution satisfying the given condition:
Question 11.
(x + y)dy + (x – y)dx = 0, y = 1, when x = 1.
Solution:
(x + y)dy + (x – y)dx
or (x + y) dy = – (x – y) dx
∴ \(\frac{dy}{dx}\) = – \(\frac{x-y}{x+y}\) = f(x, y).
f(x, y) is a homogeneous function.

Put v2 + 1 = t so that 2v dv = dt
or \(\frac{1}{2}\) ∫\(\frac{dt}{t}\) + tan-1 v = – log x + C
or \(\frac{1}{2}\)log t + tan-1v = – log x + C
or \(\frac{1}{2}\)log(v2 + 1) + tan-1 v = – log x + C
Put v = \(\frac{y}{x}\) and obtain:

Put x = 1, y = 1 and obtain:
\(\frac{1}{2}\)log(1 + 1) + tan-1\(\frac{1}{1}\) = C
or \(\frac{1}{2}\)log 2 + \(\frac{π}{4}\) = C
Putting value of C in (1). The particular solution is
\(\frac{1}{2}\)log(x2 + y2) + tan-1(\(\frac{y}{x}\))
= \(\frac{1}{2}\) log 2 + \(\frac{π}{4}\).
![]()
Question 12.
x2dy + (xy + y2)dx = 0, y = 1, when x = 1.
Solution:
x2dy + (xy + y2) dx = 0
∴ \(\frac{dy}{dx}\) = \(\frac{x y+y^{2}}{x^{2}}\) = f(x, y)
f(x, y) is homogeneous
∴ Put y = vx, so that \(\frac{dy}{dx}\) = v + x \(\frac{dv}{dx}\).
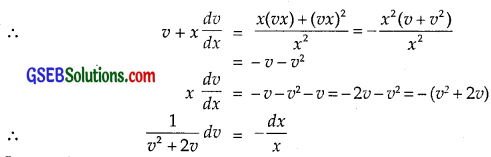
Integrating, we get

Putting v = \(\frac{y}{x}\), we get
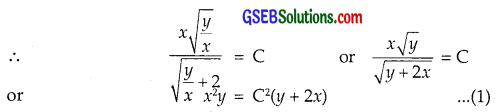
Putting x = 1, y = 1, we get
1 = C2(1 + 2) ∴ C2 = \(\frac{1}{3}\).
Putting C2 = \(\frac{1}{3}\) in (1), we get
x2y = \(\frac{1}{3}\)(y + 2x)
∴ Particular solution is 3x2y = y + 2x.
Question 13.
(x sin2 \(\frac{y}{x}\) – y) dx + x dy = 0, y = \(\frac{π}{4}\), when x = 1.
Solution:
[x sin2 \(\frac{y}{x}\) – y] dx + x dy = 0
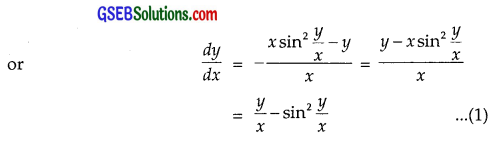
which is homogeneous
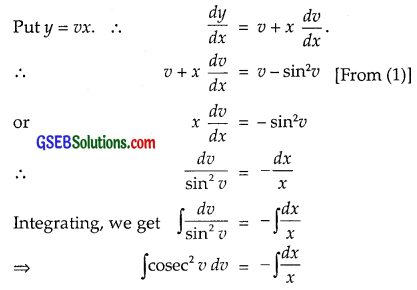
⇒ – cot v = – log x + C
⇒ + log x – cot v = C
Putting v = \(\frac{y}{x}\), we get the general solution as
log x – cot \(\frac{y}{x}\) = C.
Putting x = 1 and y = \(\frac{π}{4}\), we get
log 1 – cot \(\frac{π}{4}\) = C or 0 – 1 = C ⇒ C = – 1.
∴ Particular solution is
log x – cot \(\frac{y}{x}\) = – 1 or cot \(\frac{y}{x}\) – log x = 1.
![]()
Question 14.
\(\frac{dy}{dx}\) – \(\frac{y}{x}\) + cosec (\(\frac{y}{x}\)) = 0, y = 0, when x = 1.
Solution:
We have:
\(\frac{dy}{dx}\) – \(\frac{y}{x}\) + cosec \(\frac{y}{x}\) = 0 ……………. (1)
Put y = vx, so that \(\frac{dy}{dx}\) = v + x \(\frac{dv}{dx}\). ………………….. (2)
From (1) and (2), we get
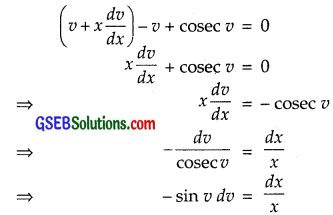
Integrating both sides, we get
∫(- sin v)dv = ∫\(\frac{dx}{x}\)
⇒ cos v = log |x| + C
⇒ cos \(\frac{y}{x}\) = log|x| + C
It is given that y(1) = 0, i.e; when x = 1, y = 0.
∴ cos 0 = log|1| + C
⇒ 1 = 0 + C ⇒ C = 1.
∴ cos \(\frac{y}{x}\) = log |x| + 1
⇒ log |x| = cos \(\frac{y}{x}\) – 1, (x ≠ 0)
which is the required particular solution.
![]()
Question 15.
2 xy + y2 – 2x2 \(\frac{dy}{dx}\) = 0, y = 2, when x = 1.
Solution:
We have: 2xy + y2 – 2x2 \(\frac{dy}{dx}\) = 0
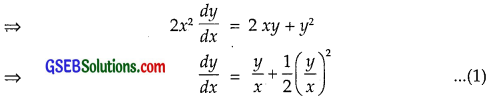
which is a homogeneous differential equation.
Put y = vx. Then \(\frac{dy}{dx}\) = v + x \(\frac{dv}{dx}\).
∴ (1) becomes v + x \(\frac{dv}{dx}\) = v + \(\frac{1}{2}\)v2
⇒ x \(\frac{dv}{dx}\) = \(\frac{1}{2}\) v2 ⇒ \(\frac{2}{v^{2}}\)dv = \(\frac{dx}{x}\).
Integrating both sides, we get

It is given that y(1) = 2, i.e., when x = 1, y = 2.

which is the required particular solution.
Choose the correct answers in the following questions 16 and 17:
Question 16.
A homogeneous differential equation of the form \(\frac{dx}{dy}\) = h(\(\frac{x}{y}\)) can be solved by making the substitution.
(A) y = vx
(B) v = yx
(C) x = vy
(D) x = v
Solution:
For solving the homogeneous equation of the form \(\frac{dx}{dy}\) = h(\(\frac{x}{y}\)), we make the substitution x = vy.
∴ Part (C) is the correct answer.
![]()
Question 17.
Which of the following is a homogeneous differential equation?
(A) (4x + 6y + 5)dy – (3y + 2x + 4) dx = 0
(B) xy dx – (x3 + y3)dy = 0
(C) (x3 + 2y2) dx + 2xy dy = 0
(D) y2dx + (x2 – xy – y2) dy = 0
Solution:
Consider the differential equation
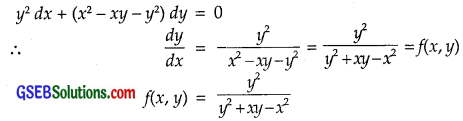
Replacing x by λx by λy, we get

∴ f(x, y) is the homogeneous function of degree zero.
Hence, part (D) is the correct answer.