GSEB Solutions Class 12 Maths Chapter 10 Vector Algebra Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 10 Vector Algebra Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 10 Vector Algebra Miscellaneous Exercise

Question 1.
Write down a unit vector in XY plane making an angle of 30° with the positive direction of x-axis.
Solution:
Let OX, OY, OZ be the coordinate axes. The line OP lies in the plane XY so that ∠XOP = 30°, ∠POY = 60° and ∠POZ = 90°.
∴ Direction angles of OP are 30°, 60° and 90°.
∴ Direction cosines of OP are cos 30°, cos 60° and cos 90°.

Question 2.
Find the scalar components and magnitude of the vector joining the points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂).
Solution:
Positive vectors of P and Q are x₁\(\hat {i} \) + y₁\(\hat {j} \) + z₁\(\hat {k} \)
and x₂\(\hat {i} \) + y₂\(\hat {j} \) + z₂\(\hat {k} \) respectively.
∴ \(\overrightarrow{\mathrm{PQ}}\) = \(\overrightarrow{\mathrm{OQ}}\) – \(\overrightarrow{\mathrm{OP}}\)
= (x₂\(\hat {i} \) + y₂\(\hat {j} \) + z₂\(\hat {k} \)) – (x₁\(\hat {i} \) + y₁\(\hat {j} \) + z₁\(\hat {k} \))
= (x₂ – x₁)\(\hat {i} \) + (y₂ – y₁)\(\hat {j} \) + (z₂ – z₁)\(\hat {k} \)
∴ Scalar components of vector \(\overrightarrow{\mathrm{PQ}}\) are x₂ – x₁, y₂ – y₁ and z₂ – z₁
Further, |\(\overrightarrow{\mathrm{PQ}}\)| = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\).

Question 3.
A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops.
Determine the girl’s displacement from her initial point of departure.
Solution:
The girl walks 4 km westward. This is represented by vector \(\overrightarrow{\mathrm{OQ}}\) = 4\(\hat {i} \) …………….. (1)
Further she goes in the direction 30° east of north, i.e., she moves along PQ and stops at Q. PQ makes x-4 an angle of 60° with OP.

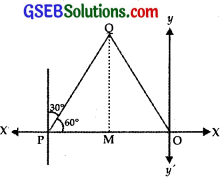
Scalar components of PQ along OX = PQ cos 60° = 3 cos 60° = \(\frac{3}{2}\).
Scalar vertical component of PQ along OY = 3 sin 60° = \(\frac{3 \sqrt{3}}{2}\).
∴ \(\overrightarrow{\mathrm{PQ}}\) = \(\frac{3}{2}\)\(\hat {i} \) + \(\frac{3 \sqrt{3}}{2}\)\(\hat {j} \) ……………… (2)
Thus, the girl walks along OP and then along PQ.
∴ \(\overrightarrow{\mathrm{OP}}\) + \(\overrightarrow{\mathrm{PQ}}\) =\(\overrightarrow{\mathrm{OQ}}\)
From (1) and (2),

Question 4.
If \(\vec {a}\) = \(\vec {b}\) + \(\vec {c}\), then is it true that |\(\vec {a}\)| = |\(\vec {b}\)| + |\(\vec {c}\)|?
Justify your answer.
Solution:
\(\vec {a}\) = \(\vec {b}\) + \(\vec {c}\)
|\(\vec {a}\)| = |\(\vec {b}\) + \(\vec {c}\)|
∴ |\(\vec {a}\)|² = |\(\vec {b}\) + \(\vec {c}\)|² = (\(\vec {b}\) + \(\vec {c}\)) . (\(\vec {b}\) + \(\vec {c}\))
= \(\vec {b}\).\(\vec {b}\) + \(\vec {b}\).\(\vec {c}\) + \(\vec {c}\).\(\vec {b}\) + \(\vec {c}\).\(\vec {c}\)
= |\(\vec {b}\)|² + 2\(\vec {b}\).\(\vec {c}\) + |\(\vec {c}\)|² [∵ \(\vec {b}\).\(\vec {c}\) = \(\vec {c}\).\(\vec {b}\)]
= |\(\vec {b}\)|² + |\(\vec {c}\)|² + 2|\(\vec {b}\)| |\(\vec {c}\)| cos θ,
where θ is the angle between \(\vec {b}\) and \(\vec {c}\).
When θ = 0° |\(\vec {a}\)|² = |\(\vec {b}\)|² + |\(\vec {c}\)|² + 2|\(\vec {b}\)| |\(\vec {c}\)| = (|\(\vec {b}\)| + |\(\vec {c}\)|²
⇒ |\(\vec {a}\)| = |\(\vec {b}\)| + |\(\vec {c}\)|
If θ ≠ 0°, |\(\vec {a}\)| ≠ |\(\vec {b}\)| + |\(\vec {c}\)|.

Question 5.
Find the value of x for which x (\(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \)) is a unit vector.
Solution:
Let \(\vec {a}\) = x(\(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \)) = x\(\hat {i} \) + x\(\hat {j} \) + x\(\hat {k} \)
|\(\vec {a}\)| = \(\sqrt{x^{2}+x^{2}+x^{2}}\) = \(\sqrt{3}\)x
But |x| = 1 ⇒ \(\sqrt{3}\)x = ± 1 ∴ x = ± \(\frac{1}{\sqrt{3}}\).

Question 6.
Find a vector of magnitude 5 units and parallel to the resultant of the vectors \(\vec {a}\) = 2\(\hat {i} \) + 3\(\hat {j} \) – \(\hat {k} \)
and \(\vec {b}\) = \(\hat {i} \) – 2\(\hat {j} \) + \(\hat {k} \).
Solution:
Let vector c be the resultant of \(\vec {a}\) and \(\vec {b}\).
Now, \(\vec {c}\) = \(\vec {a}\) + \(\vec {b}\)
= (2\(\hat {i} \) + 3\(\hat {j} \) – \(\hat {k} \)) + (\(\hat {i} \) – 2\(\hat {j} \) + \(\hat {k} \)) = 3\(\hat {i} \) + \(\hat {j} \)
⇒ |\(\vec {c}\)| = \(\sqrt{3^{2}+1^{2}\) = \(\sqrt{10}\).

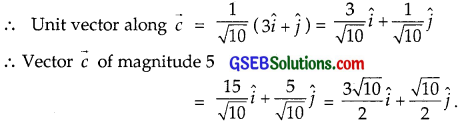
Question 7.
If \(\vec {a}\) = \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \), \(\vec {b}\) = 2\(\hat {i} \) – \(\hat {j} \) + 3\(\hat {k} \)
and \(\vec {c}\) = \(\hat {i} \) – 2\(\hat {j} \) + \(\hat {k} \), find a unit vector parallel to the vector 2\(\vec {a}\) – \(\vec {b}\) + 3\(\vec {c}\).
Solution:
We have:
\(\vec {a}\) = \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \), \(\vec {b}\) = 2\(\hat {i} \) – \(\hat {j} \) + 3\(\hat {k} \)
\(\vec {c}\) = \(\hat {i} \) – 2\(\hat {j} \) + \(\hat {k} \)
∴ \(\vec {d}\) – 2\(\vec {a}\) – \(\vec {b}\) + 3\(\vec {c}\)
= 2(\(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \)) – (2\(\hat {i} \) – \(\hat {j} \) + 3\(\hat {k} \)) + 3(\(\hat {i} \) – 2\(\hat {j} \) + \(\hat {k} \))
= 2\(\hat {i} \) + 2\(\hat {j} \) + 2\(\hat {k} \) – 2\(\hat {i} \) + \(\hat {j} \) – 3\(\hat {k} \) + 3\(\hat {i} \) – 6\(\hat {j} \) + 3\(\hat {k} \)
= (2 – 2 + 3)\(\hat {i} \) + (2 + 1 – 6)\(\hat {j} \) + (2 – 3 + 3)\(\hat {k} \)
= 3\(\hat {i} \) – 3\(\hat {j} \) + 2\(\hat {k} \)
∴ |\(\vec {d}\)| = \(\sqrt{3^{2}+(-3)^{2}+2^{2}}\) = \(\sqrt{9+9+4}\) = \(\sqrt{22}\).
∴ Unit vector parallel to 2\(\vec {a}\) – \(\vec {b}\) + 3\(\vec {c}\) = \(\frac{3}{\sqrt{22}}\)\(\hat {i} \) – \(\frac{3}{\sqrt{22}}\)\(\hat {j} \) + \(\frac{2}{\sqrt{22}}\)\(\hat {k} \).

Question 8.
Show that the points A(1, – 2, – 8), B(5, 0, – 2) and C(11, 3, 7) are collinear and find the ratio in which B divides AC.
Solution:
The position vectors of A and C are \(\hat {i} \) – 2\(\hat {j} \) – 8\(\hat {k} \) and 11\(\hat {i} \) + 3\(\hat {j} \) + 7\(\hat {k} \) respectively.
Let the point B lying on AC divides it in ratio λ : 1
∴ Position vector of B is

⇒ A, B and C are collinear and B divides it in the ratio 2 : 3.

Alternate Method of collinearity:

So, A, B and C are collinear.

Question 9.
Find the position vector of a point R which divides the line segment joining the two points P and Q, whose position vectors are (2\(\vec {a}\) + \(\vec {b}\)) and (\(\vec {a}\) – 3\(\vec {b}\)),
externally in the ratio 1 : 2. Also, show that P is the middle point of line segment RQ.
Solution:
The position vector of P and Q are respectively (2\(\vec {a}\) + \(\vec {b}\)) and (\(\vec {a}\) – 3\(\vec {b}\)).
R divides PQ externally in the ratio 1 : 2.

⇒ P is the mid-point of RQ and the point R is 3\(\vec {a}\) + 5\(\vec {b}\).

Question 10.
Two adjacent sides of a parallelogram are 2\(\hat {i} \) – 4\(\hat {j} \) + 5\(\hat {k} \) and \(\hat {i} \) – 2\(\hat {j} \) – 3\(\hat {k} \).
Find the unit vector parallel to its diagonal. Also, find its area.
Solution:
The adjacent sides of a parallelogram are \(\vec {a}\) = 2\(\hat {i} \) – 4\(\hat {j} \) + 5\(\hat {k} \) and \(\vec {b}\) = \(\hat {i} \) – 2\(\hat {j} \) – 3\(\hat {k} \).
∴ Its diagonal is \(\vec {a}\) + \(\vec {b}\) = (2\(\hat {i} \) – 4\(\hat {j} \) + 5\(\hat {k} \)) + (\(\hat {i} \) – 2\(\hat {j} \) – 3\(\hat {k} \))
= 3\(\hat {i} \) – 6\(\hat {j} \) + 2\(\hat {k} \).
|\(\vec {a}\) + \(\vec {b}\)| = |3\(\hat {i} \) – 6\(\hat {j} \) + 2\(\hat {k} \)| = \(\sqrt{3^{2}+(-6)^{2}+2^{2}}\)
= \(\sqrt{9+36+4}\) = 7.
∴ Unit vector parallel to diagonal of the parallelogram is \(\frac{1}{7}\)(3\(\hat {i} \) – 6\(\hat {j} \) + 2\(\hat {k} \)) or \(\frac{3}{7}\)\(\hat {i} \) – \(\frac{6}{7}\)\(\hat {j} \) + \(\frac{2}{7}\)\(\hat {k} \).

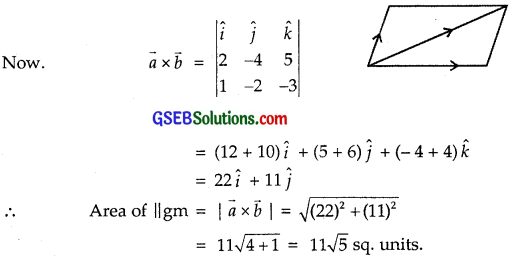
Thus, the unit vector parallel to its diagonal is \(\frac{1}{7}\)(3\(\hat {i} \) – 6\(\hat {j} \) + 2\(\hat {k} \)) and area of || gm is 11\(\sqrt{5}\) sq.units.

Question 11.
Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\) and \(\frac{1}{\sqrt{3}}\) respectively.
Solution:
Let a₁, a₂, a₃ are the direction ratios of the vector.
Now, vector is equally inclined to the axes.
∴ a₁ = a₂ = a₃ = p (say)
⇒ \(\vec {a}\) = p\(\hat {i} \) + p\(\hat {j} \) + p\(\hat {k} \)

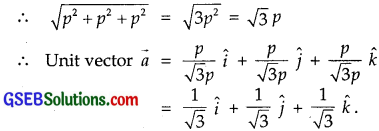
Hence, \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\), \(\frac{1}{\sqrt{3}}\) are the direction cosines of the line equally inclined to the axes.

Question 12.
Let \(\vec {a}\) = \(\hat {i} \) + 4\(\hat {j} \) + 2\(\hat {k} \), \(\vec {b}\) = 3\(\hat {i} \) – 2\(\hat {j} \) + 7\(\hat {k} \) and \(\vec {c}\) = 2\(\hat {i} \) – \(\hat {j} \) + 4\(\hat {k} \).
Find a vector \(\vec {d}\) which is perpendicular to both \(\vec {a}\) and \(\vec {b}\) and \(\vec {c}\).\(\vec {d}\) = 15.
Solution:
Let the vector \(\vec {d}\) be d₁\(\hat {i} \) + d₂\(\hat {j} \) + d₃\(\hat {k} \).
Vector \(\vec {d}\) is perpendicular to vector \(\vec {a}\) = \(\hat {i} \) + 4\(\hat {j} \) + 2\(\hat {k} \)
⇒ d₁ + 4d₂ + 2d₃ = 0 ……………… (1)
Again vector \(\vec {d}\) is perpendicular to vector \(\vec {b}\) = 3\(\hat {i} \) – 2\(\hat {j} \) + 7\(\hat {k} \)
∴ 3d₁ – 2d₂ + 7d₃ = 0 ……………….. (2)
From (1) and (2),

Question 13.
The scalar product of vector \(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \) with a unit vector along the sum of vectors
2\(\hat {i} \) + 4\(\hat {j} \) – 5\(\hat {k} \) and λ\(\hat {i} \) + 2\(\hat {j} \) + 3\(\hat {k} \) is equal to 1. Find the value of λ.
Solution:
Sum of the vectors 2\(\hat {i} \) + 4\(\hat {j} \) – 5\(\hat {k} \) and λ\(\hat {i} \) + 2\(\hat {j} \) + 3\(\hat {k} \)
= (2\(\hat {i} \) + 4\(\hat {j} \) – 5\(\hat {k} \)) + (λ\(\hat {i} \) + 2\(\hat {j} \) + 3\(\hat {k} \))
= (2 + λ)\(\hat {i} \) + 6\(\hat {j} \) – 2\(\hat {k} \) = \(\vec {s}\) (say)

⇒ λ + 6 = r
⇒ (λ + 6)² = r² = (λ² + 4λ + 44) [From (1)]
⇒ λ² + 12λ + 36 = λ² + 4λ + 44
⇒ 8λ = 44 – 36 = 8
⇒ λ = 1.

Question 14.
If \(\vec {a}\), \(\vec {b}\) and \(\vec {c}\) are mutually perpendicular vectors of equal magnitude, show that the vectors \(\vec {a}\) + \(\vec {b}\) + \(\vec {c}\) is equally inclined to \(\vec {a}\), \(\vec {b}\) and \(\vec {c}\).
Solution:
|\(\vec {a}\)| = |\(\vec {b}\)| = |\(\vec {c}\)| = λ(say) ……………… (1)
Also, \(\vec {a}\), \(\vec {b}\) and \(\vec {c}\) are mutually perpendicular.
∴ \(\vec {a}\).\(\vec {b}\) = 0, \(\vec {b}\).\(\vec {c}\) = 0 and \(\vec {a}\) + \(\vec {c}\) = 0 ……………… (2)
Let θ be the angle between vectors \(\vec {a}\) and \(\vec {a}\) + \(\vec {b}\) + \(\vec {c}\).

Question 15.
Prove that (\(\vec {a}\) + \(\vec {b}\)).(\(\vec {a}\) + \(\vec {b}\)) = |\(\vec {a}\)|² + |\(\vec {b}\)|²,
if any and only if \(\vec {a}\) and \(\vec {b}\) are perpendicular to each other, given that \(\vec {a}\) ≠ 0, \(\vec {b}\) ≠ 0.
Solution:
(\(\vec {a}\) + \(\vec {b}\)).(\(\vec {a}\) + \(\vec {b}\)) = \(\vec {a}\).(\(\vec {a}\) + \(\vec {b}\)) + \(\vec {b}\).(\(\vec {a}\) + \(\vec {b}\))
= \(\vec {a}\).\(\vec {a}\) + \(\vec {a}\).\(\vec {b}\) + \(\vec {b}\).\(\vec {a}\) + \(\vec {b}\).\(\vec {b}\)
= |\(\vec {a}\)|² + \(\vec {a}\).\(\vec {b}\) + \(\vec {b}\).\(\vec {a}\) + |\(\vec {b}\)|²
= |\(\vec {a}\)|² + |\(\vec {b}\)|² + 2\(\vec {a}\)\(\vec {b}\) [∵ \(\vec {b}\).\(\vec {a}\) = \(\vec {a}\).\(\vec {b}\)

(i) Let \(\vec {a}\) ⊥ \(\vec {b}\). So, \(\vec {a}\).\(\vec {b}\) = 0.
∴ (\(\vec {a}\) + \(\vec {b}\)).(\(\vec {a}\) + \(\vec {b}\)) = |\(\vec {a}\)|² + |\(\vec {b}\)|² + 2\(\vec {a}\) \(\vec {b}\)
= |\(\vec {a}\)|² + |\(\vec {b}\)|² [∵ \(\vec {a}\).\(\vec {b}\) = 0]
Again if \(\vec {a}\) is not perpendicular to \(\vec {b}\) ⇒ \(\vec {a}\).\(\vec {b}\) ≠ 0.
Now, (\(\vec {a}\) + \(\vec {b}\)).(\(\vec {a}\) + \(\vec {b}\)) = |\(\vec {a}\)|² + |\(\vec {b}\)|² + 2 \(\vec {a}\) \(\vec {b}\)
≠ |\(\vec {a}\)|² + |\(\vec {b}\)|²
unless \(\vec {a}\).\(\vec {b}\) = 0.
Hence, \(\vec {a}\).\(\vec {b}\) = 0 or vector \(\vec {a}\) is perpendicular to \(\vec {b}\).

Choose the correct answers in questions 16 to 19:

Question 16.
If θ is the angle between two vectors \(\vec {a}\) and \(\vec {b}\), then \(\vec {a}\), \(\vec {b}\) ≥ 0 only, when
(A) 0 < θ < \(\frac{π}{2}\)
(B) θ = \(\frac{π}{3}\)
(C) θ = \(\frac{π}{2}\)
(D) 0 ≤ θ ≤ π
Solution:
\(\vec {a}\).\(\vec {b}\) ≥ 0 ⇒ |\(\vec {a}\)| |\(\vec {b}\)| cos θ ≥ 0
Now, |\(\vec {a}\)| = +ve, |\(\vec {b}\)| = +ve ⇒ cos θ ≥ 0
Therefore, 0 ≤ θ ≤ \(\frac{π}{2}\)
∴ Part (B) is the correct answer.

Question 17.
Let \(\vec {a}\) and \(\vec {b}\) be two unit vectors and θ be the angle between them. Then, \(\vec {a}\) + \(\vec {b}\) is a unit vector, if
(A) θ = \(\frac{π}{4}\)
(B) θ = \(\frac{π}{3}\)
(C) θ = \(\frac{π}{2}\)
(D) θ = \(\frac{2π}{3}\)
Solution:
We have:
|\(\vec {a}\)| = 1, |\(\vec {b}\)| = 1
and |\(\vec {a}\) + \(\vec {b}\)| = 1, or |\(\vec {a}\) + \(\vec {b}\)|² = 1.
i.e. (\(\vec {a}\) + \(\vec {b}\)). (\(\vec {a}\) + \(\vec {b}\)) = 1
or |\(\vec {a}\)|² + |\(\vec {b}\)|² + 2\(\vec {a}\)\(\vec {b}\) = 1 [ \(\vec {b}\).\(\vec {a}\) = \(\vec {a}\).\(\vec {b}\)]
= 1 + 1 + 2|\(\vec {a}\)| |\(\vec {b}\)| cos θ = 1
[∵ |\(\vec {a}\)| = 1, |\(\vec {b}\)| = 1],
where θ is the angle between \(\vec {a}\) and \(\vec {b}\).
∴ 2 + 2 . 1 . cos θ = 1
or 2 cos θ = 1 ⇒ cos θ = – \(\frac{1}{2}\)
⇒ θ = \(\frac{2π}{3}\).
∴ Part (D) is the correct answer.

Question 18.
The value of \(\hat {i} \).(\(\hat {j} \) × \(\hat {k} \)) + \(\hat {j} \).(\(\hat {i} \) × \(\hat {j} \)) is
(A) 0
(B) \(\frac{π}{4}\)
(C) \(\frac{π}{2}\)
(D) π
Solution:
(\(\hat {i} \) + \(\hat {j} \) + \(\hat {k} \)) are the perpendicular unit vectors, we know that
\(\hat {i} \) × \(\hat {j} \) = \(\hat {k} \), \(\hat {j} \) × \(\hat {k} \) = \(\hat {i} \), \(\hat {k} \) × \(\hat {i} \) = \(\hat {j} \)
and \(\hat {i} \).\(\hat {i} \) = 1, \(\hat {j} \).\(\hat {j} \) = 1 and \(\hat {k} \).\(\hat {k} \) = 1
⇒ \(\hat {i} \).(\(\hat {j} \) × \(\hat {k} \)) + \(\hat {j} \).(\(\hat {k} \) × \(\hat {i} \)) + \(\hat {k} \).(\(\hat {i} \) × \(\hat {j} \))
= \(\hat {i} \).(\(\hat {j} \) × \(\hat {k} \)) – \(\hat {j} \).(\(\hat {k} \) × \(\hat {i} \)) + \(\hat {k} \).(\(\hat {i} \) × \(\hat {k} \))
[∵ \(\hat {i} \) × \(\hat {k} \) = – \(\hat {k} \) × \(\hat {i} \)]
= \(\hat {i} \).\(\hat {i} \) – \(\hat {j} \).\(\hat {j} \) + \(\hat {k} \).\(\hat {k} \) = 1 – 1 + 1 = 1.
∴ Part (C) is the correct answer.

Question 19.
If θ is the angle between any two vectors \(\vec {a}\) and \(\vec {b}\), then |\(\vec {a}\).\(\vec {b}\)| = |\(\vec {a}\) × \(\vec {b}\)|, when θ is equal to
(A) 0
(B) \(\frac{π}{4}\)
(C) \(\frac{π}{2}\)
(D) π
Solution:
θ is angle between vectors \(\vec {a}\) and \(\vec {b}\)
∴ |\(\vec {a}\).\(\vec {b}\)| = |\(\vec {a}\)| |\(\vec {b}\)| |cos θ|
and |\(\vec {a}\) × \(\vec {b}\)| = |\(\vec {a}\)| |\(\vec {b}\)| |sin θ|
We have: |\(\vec {a}\).\(\vec {b}\)| = |\(\vec {a}\) × \(\vec {b}\)|
∴ |\(\vec {a}\)| |\(\vec {b}\)| |cos θ| = |\(\vec {a}\)| |\(\vec {b}\)| |sin θ|
⇒ |cos θ| = |sin θ|
or |tan θ| = 1 or tan θ = 1
⇒ θ = \(\frac{π}{4}\).
∴ Part (B) is the correct answer.