Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3
![]()
Question 1.
Find the slope of the tangent to the curve y = 3x4 – 4x at x = 4.
Solution:
The curve is y = 3r4 – 4x.
∴ \(\frac { dy }{ dx }\) = 12x³ – 4.
∴ Slope of the tangent at x = 4 is
(\(\frac { dy }{ dx }\))x=4 = 12 x 4³ – 4 = 764.
Question 2.
Find the slope of the tangent to the curve y = \(\frac { x – 1}{ x-2 }\), x ≠ 2 at x = 10.
Solution:
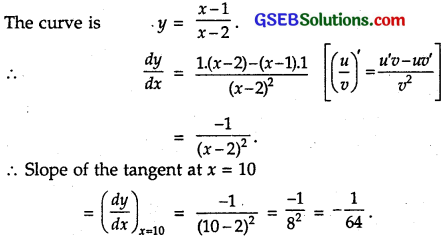
Question 3.
Find the slope of the tangent to the curve y = x³ – x + 1 at the point whose x-coordinate is 2.
Solution:
The curve is y = x³ – x + 1.
∴ \(\frac { dy }{ dx }\) = 3x² – 4.
∴ Slope of the tangent at x = 2
(\(\frac { dy }{ dx }\))x=2 = 3 x 2² – 1 = 11.
![]()
Question 4.
Find the slope of the tangent to the curve y = x³ – 3x + 2 at the point whose x-coordinate is 3.
Solution:
The curve is y = x³ – 3x + 2
∴ \(\frac { dy }{ dx }\) = 3x² – 3.
∴ Slope of the tangent at x = 3
(\(\frac { dy }{ dx }\))x=3 = 3 . 3² – 3 = 24.
Question 5.
Find the slope of the normal to the curve x = a cos³θ, y = a sin³θ at θ = \(\frac { π }{ 4 }\).
Solution:
Equation of the curve is x = a cos³θ, y = a sin³θ.
Differentiating w.r.t. θ, we get
\(\frac { dx }{ dθ }\) = – 3a cos² θ, \(\frac { dy }{ dθ }\) = 3a sin²θ cosθ
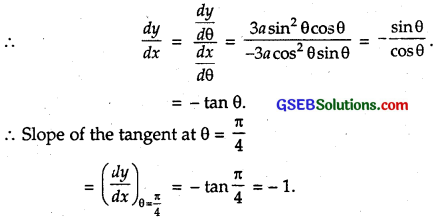
Hence, slope of the normal = – \(\frac { 1 }{ m }\) = \(\frac { -1 }{ -1 }\) = 1.
Question 6.
Find the slope of the normal to the curve x = 1 – a sin θ, y = b cos² θ at θ = \(\frac { π }{ 2 }\).
Solution:
The equation of curve is x = 1 – a sin θ, y = b cos²θ.

Question 7.
Find points at which the tangent to the curve y = x³ – 3x² – 9x + 7 is parallel to the x-axis.
Solution:
Equation of the curve is y = x³ – 3x² – 9x + 7.
Differentiating w.r.t. x, we get
\(\frac { dy }{ dx }\) = 3x² – 6x – 9 = 3(x² – 2x – 3)
Tangent is parallel to x-axis, if the slope = 0 or \(\frac { dy }{ dx }\) = 0.
⇒ 3(x – 3)(x + 1) = 0
∴ x = – 1, 3.
When x = – 1, y = (- 1)³ – 3(- 1)² – 9(- 1) + 7
= – 1 – 3 + 9 + 7 = 12.
When x = 3, y = 3³ – 3.3² – 9 . 3 + 7
= 27 – 27 – 27 + 7 = – 20.
Hence, the tangent to the given curve are parallel to x-axis at the points (- 1, – 12) and (3, – 20).
![]()
Question 8.
Find a point on the curve y = (x – 2)² at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Solution:
The equation of the curve is
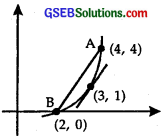
y = (x – 2)²
Differentiating w.r.t. x, we get
\(\frac { dy }{ dx }\) = 2(x – 2)
The points A and B are (2, 0) and (4, 4) respectively :
∴ Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) = \(\frac { 4-0 }{ 4-2 }\)
= \(\frac { 4 }{ 2 }\) = 2
Slope of the tangent = 2(x – 2)
Equating (1) and (2), we get
2(x – 2) = 2
∴ x – 2 = 1 or x = 3.
When x = 3, y = (3 – 2)² = 1.
Hence, the tangent is parallel to the chord AB at (3, 1).
Alternatively : By MVT,
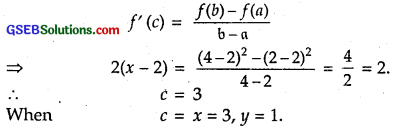
Hence, the result.
Question 9.
Find the point on the curve y = x³ – 11x + 5 at which the tangent is y = x – 11.
Solution:
Equation of the curve is
y = x³ – 11x + 5.
Differentiating w.r.t. x, we get
\(\frac { dy }{ dx }\) = 3x² – 11 … (1)
Also, the slope of the tangent y = x – 11
= coeff. of x = 1 … (2)
Equating (1) and (2), we get
3x² – 11 = 1.
∴ 3x² = 12.
⇒ x² = 4, x = ± 2.
When x = 2, y = x – 11 = 2 – 11 = – 9.
When x = -2, y = x – 11 = – 2 – 11 = – 13.
But (- 2, – 13) does not lie on the curve.
∴ y = x – 11 is the tangent at (2, – 9).
Question 10.
Find the equations of all lines having slope -1 that are tangents to the curve y = \(\frac { 1 }{ x-1 }\), x ≠ 1.
Solution:
Equation of the curve is y = \(\frac { 1 }{ x-1 }\)
Differentiating w.r.t. x,
\(\frac { dy }{ dx }\) = – \(\frac{1}{(x-1)^{2}}\)
Slope of the tangent = – 1
∴ – \(\frac{1}{(x-1)^{2}}\) = – 1.
∴ (x – 1)² = 1.
∴ x – 1 = ± 1 ⇒ x = 2 or 0.
When x = 2, y = \(\frac { 1 }{ x-1 }\) = \(\frac { 1 }{ 1 }\) = 1.
When x = 0, y = \(\frac { 1 }{ 0-1 }\) = – 1.
The points where the tangents to the given curve have the slope -1 are (2,1) and (0,- 1).
∴ Equation of the tangent at (2, 1) is
y – 1 = – 1 x (x – 2) = – x + 2
or x + y = 3.
Equation of tangent at (0, – 1) is
y + 1 = – 1 x (x – 0)
⇒ x + y + 1 = 0.
Thus, the required lines are x + y- 3 = 0 and x + y + 1 = 0.
![]()
Question 11.
Find the equations of all lines having slope 2 and that are tangents to the curve y = \(\frac { 1 }{ x-3 }\)
Solution:
The equation of the given curve is y = \(\frac { 1 }{ x-3 }\)
∴ \(\frac { dy }{ dx }\) = ( -1)(x-3)-2 = \(\frac{-1}{(x-3)^{2}}\)
But slope of tangent = 2
∴ \(\frac{-1}{(x-3)^{2}}\) = 2 ⇒ (x-3)² = – \(\frac { 1 }{ 2 }\),
Which is not possible as (x – 3)² > 0.
Thus, no tangent to the curve y = \(\frac { 1 }{ x-3 }\) has slope 2.
Question 12.
Find the equations of all lines having slope 0 and that are tangents to the curve y = \(\frac{1}{x^{2}-2 x+3}\)
Solution:
Let the tangent be at the point (x1, y1) to the curve

The tangent at {xv y,), i.e., (1, \(\frac { 1 }{ 2 }\)) having slope 0 is
y – \(\frac { 1 }{ 2 }\) = 0(x – 1) ⇒ y – \(\frac { 1 }{ 2 }\) = 0 ⇒ y = \(\frac { 1 }{ 2 }\)
Question 13.
Find the points on the curve \(\frac{x^{2}}{9}\) + \(\frac{y^{2}}{16}\) = 1 at which the tangents are (i) parallel to x-axis, (ii) parallel to y-axis.
Solution:
The equation of the curve is
\(\frac{x^{2}}{9}\) + \(\frac{y^{2}}{16}\) = 1
Differentiating w.r.t. x,
\(\frac { 2x }{ 9 }\) + \(\frac { 2y }{ 16 }\) \(\frac { dy }{ dx }\) = 0
∴ \(\frac { dy }{ dx }\) = – \(\frac { 16 }{ 9 }\) . \(\frac { x }{ y }\).
(i) If the tangent is parallel to x-axis, \(\frac { dy }{ dx }\) = 0.
∴ – \(\frac { 16 }{ 9 }\) . \(\frac { x }{ y }\) = 0 ⇒ x = 0.
Putting x = 0 in (1), we get
\(\frac{y^{2}}{16}\) = 1. ∴ y = ± 4.
Tangents are parallel to x-axis at (0, 4) and (0, – 4).
(ii) When tangents are parallel to y-axis, then denominator of \(\frac { dy }{ dx }\) is zero.
⇒ y = 0.
Putting y = 0 in (1), \(\frac{x^{2}}{9}\) = 1 ⇒ x = ± 3.
∴ Tangents are parallel to y-axis at (3, 0) and (- 3, 0).
![]()
Question 14.
Find the equations of the tangent and normal to the given curves at the indicated points :
(i) y = x4 – 6x³ + 13x² – 10x + 5 at (0, 5).
(ii) y = x4 – 6x³ + 13x² – 10x + 5 at (1, 3).
(iii) y = x³ at (1,1).
(iv) y = x² at (0, 0
(v) x = cos t, y = sin t at t = \(\frac { π }{ 4 }\).
Solution:
(i) We have : y = x4 – 6x³ + 13x² – 10x + 5
\(\frac { dy }{ dx }\) = 4x³ – 18x² + 26x – 10.
Putting x = 0, \(\frac { dy }{ dx }\) at (0, 5) = – 10.
Slope of tangent at (0, 5) = – 10.
Thus, the equation of tangent at P(0, 5) is
y – y1 = \(\frac { dy }{ dx }\)at P (x – x1)
⇒ y = 5 = – 10(x – 0)
⇒ y + 10x – 5 = 0.
Further, the equation of normal at P(0, 5) is
(x – x1) = \(\frac { dy }{ dx }\)at P (y – y1) = 0
⇒ (x – 0) + (-10)(y – 5) = 0
⇒ y – 10y + 50 = 0.
(ii) We have : y = x4 – 6x³ + 13x² – 10x + 5
\(\frac { dy }{ dx }\) = 4x³ – 18x² + 26x – 10.
Putting x = 1, \(\frac { dy }{ dx }\) = 4 – 18 + 26 – 10 = 2.
∴ Slope of tangent at (1, 3) is 2.
∴ Equation of tangent at (1, 3) is
y – 3 = 2(x – 1) ⇒ y – 3 = 2x – 2
⇒ y = 2x + 1.
Further, the equation of normal is
(x – 1) + 2 . (y – 3) = 0 ⇒ x – 1 + 2y – 6 = 0.
⇒ x + 2y – 7 = 0.
(iii) We have : y = x³ at (1,1).
∴ \(\frac { dy }{ dx }\) = 3x².
Now, \(\frac { dy }{ dx }\) at (1, 1) = 3(1)² = 3.
i.e., Slope of tangent at (1, 1) is 3.
Equation of tangent at (1, 1) is
y – 1 = 3(x – 1) ⇒ y – 1 = 3x – 3
⇒ y = 3x – 2.
Further, the equation of normal at (1, 1) is
(x – 1) + 3(y – 1) = 0 ⇒ x – 1 + 3y – 3 = 0.
⇒ x + 3y – 4 = 0.
(iv) We have : y = x²
∴ \(\frac { dy }{ dx }\) = 2x.
Now, \(\frac { dy }{ dx }\) at (0, 0) is 0.
i.e., Slope of tangent at (0, 0) is 0.
∴ Equation of tangent at (0, 0) is
y – 0 = 0(x – 0) ⇒ y = 0.
Further, the equation of normal at (0, 0) is
(x – 0) + 0(y – 0) = 0 ⇒ x = 0.
(v) Equation of the curve are x = cos t … (1) and y = sin t … (2)
At t = \(\frac { π }{ 4 }\), x = cos \(\frac { π }{ 4 }\) = \(\frac{1}{\sqrt{2}}\)
and y = sin \(\frac { π }{ 4 }\) = \(\frac{1}{\sqrt{2}}\)
∴ t = \(\frac { π }{ 4 }\) ⇒ the point is (\(\frac{1}{\sqrt{2}}\), \(\frac{1}{\sqrt{2}}\))
From (1) and (2), we have :
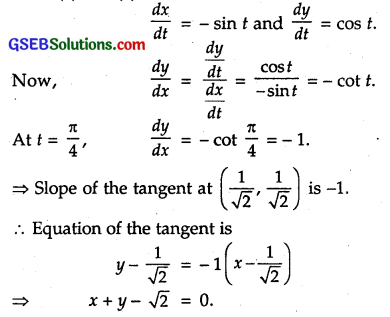
Now, slope of the normal at (\(\frac{1}{\sqrt{2}}\), \(\frac{1}{\sqrt{2}}\)) = – \(\frac { 1 }{ -1 }\) = 1.
Equation of the normal is
y – \(\frac{1}{\sqrt{2}}\) = 1(x – \(\frac{1}{\sqrt{2}}\))
⇒ y = x.
![]()
Question 15.
Find the equation of the tangent line to the curve y = x² – 2x + 7 which is
(a) parallel to the line 2x – y + 9 = 0.
(b) perpendicular to the line 5y – 15x = 13.
Solution:
Equation of the curve is y = x² – 2x + 7 … (1)
∴ \(\frac { dy }{ dx }\) = 2x – 2 = 2(x – 1)
(a) Slope of the line 2x-y + 9 = 0 is 2.
⇒ Slope of tangent = \(\frac { dy }{ dx }\) = 2(x – 1) = 2.
⇒ x – 1 = 1 ox x = 2.
Putting x = 2 in (1), we get
y = 2² – 2 . 2 + 7 = 7.
∴ Tangent parallel to 2x – y + 9 = 0 at (2, 7) is
y – 7 = 2(x – 2)
or 2x – y + 3 = 0.
(b) Tangent is perpendicular to the line 5y – 15x = 13.
⇒ Slope of tangent x slope of line = – 1,
Slope of the line = \(\frac { 15 }{ 5 }\) = 3.
Slope of tangent = 2(x – 1).
∴ 2(x – 1) x 3 = – 1
∴ x – 1 = \(\frac { – 1 }{ 6 }\) or x = 1 – \(\frac { 1 }{ 6 }\) = \(\frac { 5 }{ 6 }\).
Putting x = \(\frac { 5 }{ 6 }\) in (1), we get
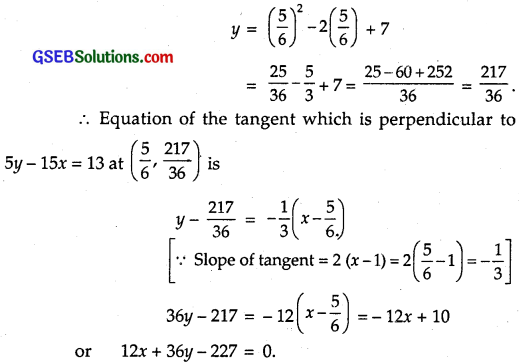
Question 16.
Show that the tangents to the curve y = 7x³ + 11 at the points, where x = 2 and x = – 2, are parallel.
Solution:
The equation of the curve is y = 7x³+ 11. … (1)
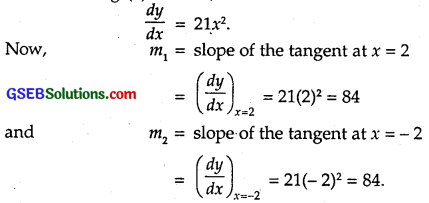
Clearly, m1 = m2.
Thus, the tangents to the given curve at the points where x = 2 and x = – 2 are parallel.
Question 17.
Find the points on the curve y = x³ at which the slope of the tangent is equal to the y – coordinate of the point.
Solution:
Let P(x1, y1) be the required point. The given curve is
y = x³
⇒ \(\frac { dy }{ dx }\) = 3x².
⇒ \(\frac { dy }{ dx }\)(x1, y1) = 3x²1.
Since the slope of the tangent at (x1, y1) = y1, therefore
3x²1 = y1 … (2)
Also, (x1, y1) lies on (1). So, y1 = x³1 … (3)
From (2) and (3), we have :
3x²1 = x³1 ⇒ x²1(3 – x1) = 0.
⇒ x1 = 0 or x1 = 3.
When x1 = 0, y1 = (0)³ = 0.
When x1 = 3, y1 = (3)³ = 27.
∴ The required points are (0, 0) and (3, 27).
![]()
Question 18.
For the curve y = 4x³ – 2x5, find all the points at which the tangents pass through the origin.
Solution:
Let (x1, y1) be the required point on the given curve
y = 4x³ – 2x5
Then, y1 = 4x³1 – 2x51 … (1)
Differentiating y = 4x³- 2×5 w.r.t. x, we get

When x1 = 0, then from (2), y1 = 0
When x1 = 1, then from (2), y1 = 4 . 1³ – 2 . 15 = 4 – 2 = 2
When x1 = – 1, then from (2), y1 = 4.(-1)³ – 2.(-1)5 = – 4 + 2 = – 2
Hence, the required points are (0, 0), (1, 2) and (- 1, – 2).
Question 19.
Find the points on the curve x² + y² – 2x = 3 at which tangents are parallel to the x-axis.
Solution:
The curve is
x² + y² – 2x – 3 = 0 … (1)
Differentiating w.r.t. x, we have :
2x + 2y \(\frac { dy }{ dx }\) – 2 = 0
⇒ 2y \(\frac { dy }{ dx }\) = 2 – 2x
⇒ \(\frac { dy }{ dx }\) = \(\frac { 1 – x }{ y }\)
Tangent is parallel to x – axis, if \(\frac { dy }{ dx }\) = 0.
i.e., if 1 – x = 0 ⇒ x=1.
Putting x = 1 in (1), we get
1 + y² – 2 – 3 = 0 ⇒ y² = 4 ⇒ y = ± 2.
Hence, the required points are (1,2) and (1, – 2), i.e., (1, ± 2).
Question 20.
Find the equation of the normal at the point (am², am³) for the curve ay² = x³.
Solution:
Equation of the curve is ay² = x³.
Differentiating w.r.t. x, we have :
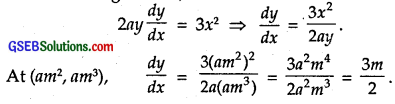
⇒ Slope of the tangent at (am², am³) is \(\frac { 3m }{ 2 }\).
and so slope of the normal at (am², am³) is \(\frac { -2 }{ 3m }\)
∴ Equation of the normal is
y – am³ = – \(\frac { 2 }{ 3m }\) (x – am²)
⇒ 3my – 3am4 = – 2x + 2am²
⇒ 2x + 3my – am²(2 + 3m²) = 0.
Question 21.
Find the equation of the normal to the curve y = x³ + 2x + 6 which is parallel to the line x + 14y + 4 = 0.
Solution:
Let the required normal be drawn at the point (x1, y1). The equation of the given curve is
y = x³ + 2x + 6 … (1)
Differentiating both sides w.r.t x, we get
\(\frac { dy }{ dx }\) = 3x² + 2
⇒ \(\frac { dy }{ dx }\)(x1, y1) = 3x²1 + 2.
Since the normal at (xt, y\) is parallel to the line x + 14y + 4 = 0. Therefore, slope of the normal at (x, y,)
= Slope of the line x + 14y + 4 = 0

Thus, the co-ordinates of the points are (2, 18) and (- 2, – 6).
The equation of the normal at (2, 18) is
y – 18 = – \(\frac { 1 }{ 14 }\) (x – 2)
⇒ 14y – 252 = – x + 2
⇒ x + 14y – 254 = 0.
The equation of the normal at (- 2, – 6) is
y + 6 = – \(\frac { 1 }{ 14 }\)(x + 2)
⇒ 14y + 84 = – x – 2
⇒ x + 14y + 86 = 0.
![]()
Question 22.
Find the equations of the tangent and normal to the parabola y² = 4ax at (at², 2at).
Solution:
The equation of the given curve is y² = 4ax. … (1)
Differentiating (1) w.r.t. x, we get

Question 23.
Prove that the curves x = y² and xy = k cut at right angles, if 8k² = 1.
Solution:
The given curves are :
x = y² … (1)
and xy = k … (2)
Putting x = y² in (2), we get
y³ = k ⇒ y = k \(\frac { 1 }{ 3 }\).
From (1), x = y² = \(\left(k^{\frac{1}{3}}\right)^{2}\) = k\(k^{\frac{2}{3}}\)
Thus, the point of intersection is (\(k^{\frac{2}{3}}\), \(k^{\frac{1}{3}}\))
Differentiating (1) w.r.t. x, we have :

Now the curves cut at right angles, if the product of slopes of tangents to two curves at (\(k^{\frac{2}{3}}\)), \(k^{\frac{1}{3}}\)) is – 1.
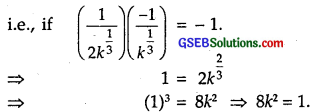
Question 24.
Find the equations of the tangent and normal to the hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 at the point (x0, y0).
Solution:

Question 25.
Find the equation of the tangent to the curve y = \(\sqrt{3x-2}\), which is parallel to the line 4x – 2y + 5 = 0.
Solution:
Let the point of contact of the tangent line parallel to the given line be P(x1, y1).
The equation of the curve is y = \(\sqrt{3x-2}\)
Differentiating both sides w.r.t. x, we get
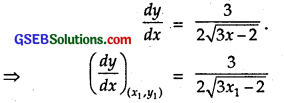
Since the tangent at (xx, is parallel to the line 4x – 2y + 5 = 0, therefore

So, the point of contact is (\(\frac { 41 }{ 8 }\), \(\frac { 3 }{ 4 }\)).
Hence, the equation of the required tangent is

Question 26.
The slope of the normal to the curve y = 2x³ + 3 sin x at x = 0 is
(A) 3
(B) \(\frac { 1 }{ 3 }\)
(C) – 3
(D) – \(\frac { 1 }{ 3 }\)
Answer:
The curve is y
= 2x² + 3 sin .t.
∴ \(\frac { dy }{ dx }\) = 4x + 3 cos x
At x = 0, \(\frac { dy }{ dx }\) = 4 x 0 + 3 cos 0 = 3. ∴ Slope = 3.
Slope of the normal is – \(\frac { 1 }{ 3 }\).
Hence, Part (D) is the correct answer.
![]()
Question 27.
The line y = x + 1 is a tangent to the curve y² = 4x at the point
(A) (1, 2)
(B) (2, 1)
(C) (1, – 2)
(D) (- 1, 2)
Solution:
The curve is y² = 4x. Therefore, 2y \(\frac { dy }{ dx }\) = 4.
∴ \(\frac { dy }{ dx }\) = \(\frac { 4 }{ 2y }\) = \(\frac { 2 }{ y }\).
Slope of the given line y = x + 1 is 1.
∴ \(\frac { 2 }{ y }\) ∴ y = 2.
Putting y = 2 in y² = 4x, we get
2² = 4 ⇒ x = 1.
Point of contact is (1, 2).
∴ Correct Answer is (A).