Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 12 Linear Programming Ex 12.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 12 Linear Programming Ex 12.1
Solve the following Linear Programming Problems graphically:
Question 1.
Maximise Z = 3x + 4y
subject to constraints: x + y ≤ 4, x ≥ 0, y ≥ 0.
Solution:
Objective function is
Z = 3x + 4y
Constraints are
x + y ≤ 4, x ≥ 0, y ≥ 0
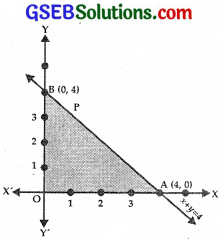
(i) consider the line
x + y = 4.
It passes through the points (4, 0) and (0, 4).
Putting x = 0, y = 0 in x + y ≤ 4, we get 0 ≤ 4 which is true.
Therefore, origin lies in the region x + y ≤ 4.
x ≥ 0 is the region to the right of y-axis and y ≥ 0 is the region on and above x-axis.
∴ The feasible region is ∆ OAB.
At (4, 0), Z = 3x + 4y = 3 × 4 + 0 = 12
At (0, 4), Z = 3x + 4y = 0 + 4 × 4 = 16
At (0, 0), Z = 0.
∴ Maximum value of Z = 16.
![]()
Question 2.
Minimise Z = – 3x + 4y
subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
Solution:
Objective function Z = – 3x + 4y
Constraints are x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
(i) Consider the line
x + 2y = 8
It passes through A(8, 0) and B(0, 4).
Putting x = 0, y = 0 in
x + 2y ≤ 8, 0 ≤ 8 which is true.
⇒ region x + 2y ≤ 8 lies on and below AB.
(ii) The line 3x + 2y = 12 passes through P(4, 0), Q(0, 6).
Putting x = 0, y = 0 in 3x + 2y ≤ 12.
⇒ 0 ≤ 12, which is true.
∴ Region 3x + 2y ≤ 12 lies on and below PQ.
(iii) x ≥ 0, the region lies on and to the right of y-axis.
(iv) y ≥ 0 lies on and above x-axis.
(v) Solving the equations x + 2y = 8 and 3x + 2y = 12,
we get x = 2, y = 3
⇒ R is (2,3), where AB and PQ intersect.
The shaded region OPRB is the feasible region.
At P(4, 0), Z = – 3x + 4y = – 12 + 0 = – 12
At R(2, 3), Z = – 6 + 12 = 6
At B(0, 4), Z = 0 + 16 = 16
At Q(0, 0), Z = 0
Thus, minimum value of Z is – 12 at P(4, 0) [Neglecting the value at (0, 0)].

![]()
Question 3.
Maximise Z = 5x + 3y.
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Solution:
The objective function is Z = 5x + 3y.
Constraints are Y
3x + 5y ≤ 15,
5x + 2y ≤ 10, x ≥ 0, y ≥ 0
(i) Consider the line 3x + 5y = 15, which passes through A(5, 0) and B(0, 3).
Putting x = 0, y = 0, in 3x + 5y ≤ 15
⇒ 0 ≤ 15 which is true.
∴ Region 3x + 5y ≤ 15 lies on and below AB.

(ii) The line 5x + 2y = 10 passes through P(2, 0) and Q(0, 5).
Put x = 0, y = 0 in 5x + 2y ≤ 10
∴ 0 ≤ 10, which is true.
Region 5x + 2y ≤ 10 lies on and below PQ.
(iii) x ≥ 0 region lies on and to the right of y-axis.
(iv) y ≥ 0 lies on and above x-axis.
(v) The feasible region is the shaded area OPRB.
Solving the equations, 3x + 5y – 15 and 5x + 2y = 10,
we get x = \(\frac{20}{19}\), y = \(\frac{45}{19}\).
⇒ AB and PQ intersect at R (\(\frac{20}{19}\), \(\frac{45}{19}\)).
At P(2, 0), Z = 5x + 3y = 10 + 0 = 10
At R(\(\frac{20}{19}\), \(\frac{45}{19}\)),
Z = \(\frac{100}{19}\) + \(\frac{135}{19}\) = \(\frac{235}{19}\)
At B(0, 3), Z = 9
At O(0, 0), Z = 0
∴ Maximum value of Z = \(\frac{235}{19}\) at (\(\frac{20}{19}\), \(\frac{45}{19}\)).
![]()
Question 4.
Minimise P = 3x + 5y
subject to x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
Solution:
The objective function is Z = 3x + 5y.
Constraints are x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
(i) consider the line
x + 3y = 3.
This passes through A(3, 0) and B(0, 1).
Putting x = 0, y = 0 in x + 3y > 3
⇒ 0 ≥ 3, which is not true.
Region x + 3y ≥ 3 lies on and above AB.
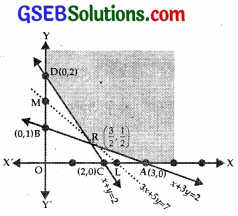
(ii) The line x + y = 2 passes through C(2, 0) and D(0, 2)
Putting x = 0, y = 0 in x + y ≥ 2
⇒ 0 ≥ 2, which is not true.
⇒ Region x + y ≥ 2 lies on and above the line CD.
(iii) x ≥ 0, this region is on and to the right of y-axis.
(iv) y ≥ 0 is on and above the x-axis.
(v) The lines x + 3y = 3 and x + y = 2 intersect at R(\(\frac{3}{2}\), \(\frac{1}{2}\)).
(vi) The feasible region is XARDY.
At A(3, 0), Z = 3x + 5y = 9 + 0 = 9.
At R(\(\frac{3}{2}\), \(\frac{1}{2}\)), Z = \(\frac{9}{2}\) + \(\frac{5}{2}\) = \(\frac{14}{2}\) = 7.
At D(0, 2), Z = 0 + 5 × 2 = 10.
∴ Minimum value of Z at R(\(\frac{3}{2}\), \(\frac{1}{2}\)) is 7.
The feasible region XARDY is unbounded. Consider the inequality 3x + 5y < 7
The line 3x + 5y = 7 passes through (\(\frac{7}{3}\), 0) and (0, \(\frac{7}{5}\)).
3x + 5y < 7 has no common point with feasible region
∴ Minimum value of Z = 7 at R(\(\frac{3}{2}\), \(\frac{1}{2}\)).
![]()
Question 5.
Maximise Z = 3x + 2y
subject to x + 2y ≥ 10, 3x + y ≤ 15, x, y ≥ 0.
Solution:
The objective function is Z = 3x + 2 y.
Constraints are x + 2y ≤ 10,
3x + y ≤ 15,
x, y ≥ 0
(i) Consider the line
x + 2 y = 10.
This line passes through A(10, 0) and B(0, 5).
Putting x = 0, y = 0 in x + 2y ≤ 10
0 ≤ 10, which is true.
⇒ x + 2y ≤ 10 lies on and below AB.
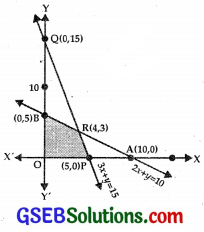
(ii) The line 3x + y = 15 passes through P(5, 0) and Q(0, 15).
Putting x = 0, y = 0 is 3x + y ≤ 15, we get 0 ≤ 15, which is true.
⇒ 3x + y ≤ 15 lies on and below PQ.
(iii) x ≥ 0 lies on and to the right of y-axis.
(iv) y ≥ 0 lies on and above x-axis.
(v) The feasible region is OPRB.
(vi) Equations are
x + 2 y = 10 …………….. (1)
3x + y = 15 ………………… (2)
Multiplying (2) by 2 to obtains
6x + 2y – 30 ……………. (3)
Subtracting (1) from (3),
5x – 20
⇒ x = 4
From (2), y = 15 – 3x = 15 -12 = 3.
Lines (1) and (2) meet at R(4, 3).
Z = 3x + 2y
Now, At P(5, 0) Z = 15 + 0 = 15
At R(4, 3) Z = 12 + 6 = 18
At B(0, 5) Z = 0 + 10 = 10
∴ Maximum value of Z = 18 at R(4, 3).
![]()
Question 6.
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that minimum of Z occurs at more than two points.
Solution:
Objective function Z = x + 2y.
Constraints are 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
(i) Consider the line
2x + y = 3.
This passes through A(\(\frac{3}{2}\), 0) and B(0, 3).

Putting x = 0, y = 0 in 2x + y ≥ 3. we get 0 ≥ 3, which is not true.
∴ The region 2x + y ≥ 3 is on and above AB.
(ii) The line x + 2y = 6 passes through P(6, 0) and B(0, 3).
Putting x = 0, y = 0 in x + 2y ≥ 6
⇒ 0 ≥ 6 which is not true.
∴ x + 2y ≥ 6 region lies on PB and above it.
(iii) x ≥ 0 lies on and to the right of y-axis.
(iv) y ≥ 0 lies on and above x-axis.
Shaded area XPBY is the feasible region.
At P(6, 0), Z = x + 2y = 6 + 0 = 6.
At B(0, 3), Z = 0 = 6 = 6
⇒ At all points on PB, Z = 6
Moreover x + 2y < 6 lies below PB which has no common point in feasible region.
Thus, the minimum value of Z is 6.
![]()
Question 7.
Minimise and Maximise Z = 5x + 10y
subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
Solution:
The objective functions is
Z = 5x + 10y.
Constraints are
x + 2y ≤ 120,
x + y ≥ 60,
x – 2y ≥ 0,
x, y ≥ 0
(i) The line x + 2y = 120 passes through A(120, 0) and 5(0, 60)
Putting x = 0, y = 0 is x + 2y ≤ 120,
we get 0 ≤ 120, which is true.
⇒ x + 2y ≤ 120 lies on AB and below AB.
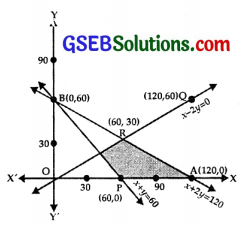
(ii) The line x + y = 60 passes through P(60, 0) and B(0, 60).
Putting x = 0 and y = 0 in x + y ≥ 60, which is not true.
⇒ x + y ≥ 60 lies on PB or above it.
(iii) The line x – 2y = 0 passes through O(0, 0) and Q(120, 60).
Putting x = 60, y = 0 in x – 2y ≥ 0, 60 ≥ 0, which is true.
⇒ x – 2y = 0 region is on QQ and below it.
(iv) x ≥ 0 lies on y-axis on its right.
(v) y ≥ 0 lies on x-axis and above it.
⇒ Feasible region is PARS which has been shaded.
![]()
Question 8.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0.
Solution:
Objective functions is Z = x + 2y.
Constraints are
x + 2y ≥ 100,
2x – y ≤ 0,
2x + y ≤ 200,
x, y ≥ 0
(i) The line x + 2y – 100, passes through A(100, 0) and B(0, 50).
Putting x = 0, y = 0 in x + y ≥ 100 or 0 ≥ 100, which is not true.
∴ Region x + 2y ≥ 100 lies on and above AB.
(ii) The line 2x – y = 0 passes through O(0, 0) and C(50, 100).
The point (0, 50) lies in the region 2x – y ≤ 0
∴ Region 2x – y ≤ 0 lies on and above OC.
(iii) The line 2x + y = 200 passes through A(100, 0) and D(0, 200).
Put x = 0, y = 0 in 2x + y ≤ 200, i.e., 0 ≤ 200, which is true.
⇒ 2x + y ≤ 200 lies on AD and below it.
(iv) x ≥ 0 lies on y-axis and on the right of it.
(v) y ≥ 0 lies on and above x-axis.
Feasible region is the shaded area BECD.
The point E is the intersection of
OC : 2x – y = 0 and AB : x + 2y = 100
i.e., The point E is (20, 40).
The point C(50, 100) lies on 2x + y = 200 and 2x – y = 0.
Now,
At B(0,50), Z = x + 2y = 100
At E(20, 40), Z = 20 + 80 = 100
At C(50, 100), Z = 50 + 200 = 250
At D(0, 200), Z = 0 + 2 × 200 = 400
Minimum value of Z = 100 at all points on the line segment joining the points B(0, 50) and E(20, 40).
Maximum value of Z = 400 at D(0, 200).
![]()
Question 9.
Maximise Z = – x + 2y, subject to constraints:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Solution:
The objective function is Z = – x + 2y. The constraints are:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0
(i) The line x + y = 5 passes through A(5, 0), B(0, 5).
Putting x = 0, y = 0 in x + y ≥ 5, we get 0 ≥ 5, which is not true.
⇒ x + y ≥ 5 lies on and above AB.
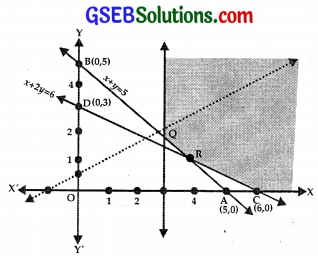
(ii) The line x + 2y = 6 passes through C(6, 0), D(0, 3).
Putting x = 0, y = 0 in x + 2y ≥ 6,
we get 0 ≥ 6, which is not true.
⇒ x + 2y ≥ 6 lies on and above CD.
(iii) x ≥ 3 lies on PQ or on the right of it.
(iv) y ≥ 0 lies on and above x-axis.
(v) The feasible region is PQRCX.
(a) Solving x = 3 and x + y = 5, we get x = 3, y = 2.
∴ These lines meet at Q(3, 2).
(b) x + y = 5 and x + 2y = 6 meet at R,
i.e., the point R is (4, 1).
At Q(3, 2), Z = – x + 2y = – 3 + 4 = 1
At R(4, 1), Z = – 4 + 2 = – 2
At C(6, 0), Z = – 6 + 0 = – 6
The maximum value of Z is 1 but the feasible region is unbounded.
Consider the inequality – x + 2y > 1
The line – x + 2y = 1 passes through (- 1, 0) and (0, \(\frac{1}{2}\)).
Putting x = 0, y = 0 in – x + 2y > 1, we get 0 > 1, which is not true.
⇒ – x + 2y > 1 lies above the line – x + 2y = 1.
∴ Feasible region of – x + 2y > 1 have many points in common.
Therefore, there is no maximum value.
![]()
Question 10.
Maximise Z = x + y subject to
x – y ≤ – 1, – x + y ≤ 0, x, y ≥ 0.
Solution:
Objective function is Z = x + y.
Constraints are x – y ≤ – 1,
– x + y ≤ 0, x, y ≥ 0.
(i) The line x – y = – 1 passes through (- 1, 0) and (0, 1).
Putting x = 0, y = 0 in x – y ≤ – 1,
we get 0 ≤ – 1 which is not true.
⇒ x – y ≤ – 1 lies on and above
AB : x – y = – 1.
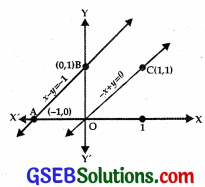
(ii) the line – x + y = 0 passes through O(0, 0) and C(1, 1).
Putting x = 0, y = 1 in – x + y ≤ 0,
we get 1 ≤ 0, which is not true.
⇒ – x + y ≤ 0 lies on and below OC.
(iii) x ≥ 0 lies on and on the right of y-axis.
(iv) y ≥ 0 lies on and above x-axis.
There is no common region, i.e., their is no feasible region.
⇒ There is no maximum value of Z.