Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 12 Linear Programming Miscellaneous Exercise Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 12 Linear Programming Miscellaneous Exercise
Question 1.
How many packets of each type of foods P and Q should be used to maximise the amount of vitamin A in the diet.
What is the maximum amount of vitamin A in the diet, if the vitamin A and different minerals contents of each food are given in the following table,
where x and y are the number of packets of foods P and Q respectively.
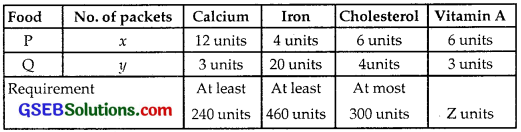
Solution:
(See Example 9 on pages 448 and 449 also).
Objective function is to maximise Z = 6x + 3y. Constraints are 12x + 3y ≥ 240, 4x + 20y ≥ 460, 6x + 4y ≤ 300, x, y ≥ 0.
(i) Consider the inequality 12x + 3y ≥ 240 or 4x + y ≥ 80.
The line 4x + y = 80 passes through A(20, 0) and B(0, 80).
Putting x = 0, y = 0 in 4x + y ≥ 80, we get 0 ≥ 80, which is not true.
⇒ 4x + y ≥ 80 lies on and above AB.

(ii) The inequality 4x + 20y ≥ 460 maybe taken as x + 5y ≥ 115.
The line x + 5y = 115 passes through C(115, 0) and D(0, 23).
Putting x = 0, y = 0, we get 0 ≥ 115, which is not true.
⇒ x + 5y ≥ 115 lies on and above CD.
(iii) For inequality 6x + 4y ≤ 300 or 3x + 2y ≤ 150, we consider the line 2x + 2y = 150 which passes through E(50, 0) and F(0, 75).
Putting x = 0, y = 0 in 3x + 2y ≤ 150, 0 ≤ 150, which is true.
⇒ 3x + 2y ≤ 150 lies on and below EF.
(iv) x ≥ 0 lies on and to the right of y-axis.
(v) y ≥ 0 lies on and above x-axis.
The shaded region PQR is the
(a) Now, consider the lines
4x + y = 80 …………….. (1)
and x + 5y = 115 ………….. (2)
Multiply equation (1) by 5 and subtract (2) from it, we get
19x = 400 – 115 = 285
∴ x = 15.
⇒ y = 80 – 4x = 80 – 4 × 15 = 20.
∴ The Point Q is (15, 20).
(b) Next, consider the lines
4x + y = 80 …………… (3)
and 3x + 2y = 150 …………… (4)
Multiply equation (3) by 2 and subtract (4) from it to get
5x = 160 – 150 = 10
∴ x = 2
∴ y = 80 – 4x = 80 – 8 = 72.
(c) Now, consider lines
x + 5y = 115 …………….. (5)
and 3x + 2 y = 150 ……………. (6)
Multiply (5) by 3 and subtract (6) from it to obtain
13y = 3 × 115 – 150 = 345 – 150 = 195
∴ y = \(\frac{195}{13}\) = 15
⇒ x = 115 – 5y = 115 – 75 = 40.
∴ The point R is (40, 15).
The objective function is Z = 6x + 3y.
At P(2, 72), Z = 12 + 3 × 72 = 12 + 216 = 228
At Q(15, 20), Z = 90 + 60 = 150
At R(40,15), Z = 240 + 45 = 285
So, 40 packets of food P and 15 packets of food Q are required to get maximum amount of vitamin A of 285 units.
![]()
Question 2.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C.
Brand Q, costing ₹200 per bag, contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C.
The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively.
Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag. What is the minimum cost of the mixture per bag?
Solution:
Let x bags of brand P and y bags of brand Q of cattle feed are mixed. Further given data is as follows:
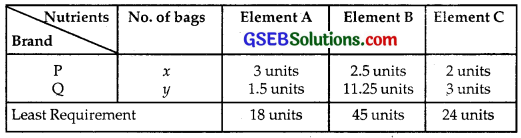
The cost of x bags of P brand and y bags of Q brand of cattle feed
= 250x + 200y
∴ The objective function is to minimise
⇒ Z = 250x + 200y
The constraints are
3x + 1.5y ≥ 18 or 2x + y ≥ 12
2.5x + 11.25y ≥ 45 or 2x + 9y ≥ 36
2x + 3y ≥ 24 and x, y ≥ 0
(i) 2x + y = 12 passes through A(6, 0) and B(0, 12).
Put x = 0, y = 0 in 2x + y ≥ 12 so that 0 ≥ 12, which is not true.
⇒ 2x + y ≥ 12 lies on and above AB.
(ii) 2x + 9y = 36 passes through C(18, 0) and D(0, 4).
Putting (0, 0) in 2x + y ≥ 12, 0 ≥ 12, which is not true.
⇒ 2x + 9y ≥ 36 lies on and above CD.
(iii) The line 2x + 3y = 24 passes through E(12, 0) and F(0, 8).
Put x = 0, y = 0 in 2x + 3y ≥ 24, we get 0 ≥ 24, which is not true.
⇒ 2x + 3y ≥ 24 lies on and above EF.
(iv) x ≥ 0 lies on and to the right of y-axis.
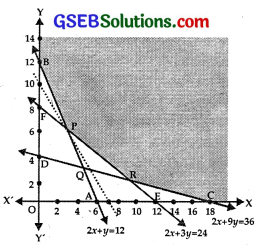
(v) y ≥ 0 lies on and above x-axis.
The shaded region YBPRCX is the feasible region P is the point of intersection of
2x + 3y = 12 …………… (1)
and 2x + 3y = 24 …………….. (2)
Subtracing (1) from (2),
2y = 12 ⇒ y = 2 ⇒ x = 9.
∴ The point P is (3, 6).
R is the point of intersection of
2x + 3y = 24 ………….. (3)
and 2x + 9y = 36 ……………….. (4)
subtracting (3) from (4), we get
6y = 12 ⇒ y = 2 ⇒ x = 9.
∴ The point R is (9, 2).
Thus, the point on the corners are
B(0, 12), P(3, 6), R(9, 2) and C(18, 0).
Now, Z = 250x + 200y
At B(0, 12), Z = 0 + 2400 = 2400
At P(3, 6), Z = 750 + 1200 = 1950
At R(9, 2), Z = 2250 + 400 = 2650
At C(18, 0) Z = 4500 + 0 = 4500
Minimum value of Z is 1950 at P(3, 6).
Feasible region is unbounded. Consider the inequality
250x + 200y < 1950.
The line 250x + 200y = 1950
or 5x + 4y = 39 passes through (\(\frac{39}{5}\), 0) and (0, \(\frac{39}{4}\)).
Also, putting x = 0, y = 0 in 5x + 4y < 39,
we get 0 < 39.
∴ 5x + 4y < 39 lies below the line 5x + 4y = 39.
There is no common point between feasible region and 5x + 4y < 39.
Hence, the minimum value of Z = 1950 at (3, 6).
⇒ The minimum cost of mixture is ₹1950, when 3 bags of brand P and 6 bags of brand Q of cattle feed are mixed.
![]()
Question 3.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains atleast 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C.
The vitamin content of one kg of each food is given below:

One kg of food X costs ₹16 and one kg of food Y costs ₹20.
∴ Z = 16x + 20y is the objective function, where Z is to be minimise.
Now, constraints are
x + 2y ≥ 10, 2x + 2y ≥ 12 or x + y ≥ 6 and 3x + y ≤ 8. x, y ≥ 0
(i) The line x + 2y = 10 passes through A(10, 0) and B(0, 5).
Putting x = 0, y = 0 in x + 2y ≥ 10, we get
0 ≥ 10, which is not true.
⇒ x + 2y ≥ 10 region lies on and above AB.
(ii) The line x + y = 6 passes through C(6, 0) and D(0, 6).
Putting x = 0, y = 0 in x + y ≥ 6, we get
0 ≥ 6, which is not true.
⇒ x + y ≥ 6 lies on and above CD.
(iii) The line 3x + y = 8 passes through E(\(\frac{8}{3}\), 0) and F(0, 8).
Putting x = 0, y = 0 in 3x + y ≥ 8, we get
0 ≥ 8, which is not true.
⇒ 3x + y ≥ 8 lies on and above EF.
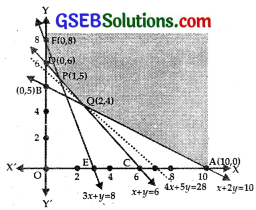
(iv) x ≥ 0 lies on and to the right of y-axis.
(v) y ≥ 0 lies on and above x-axis.
The shaded area YFPQAX represents the feasible region.
Now P is the point of intersection of the lines CD and EF, i.e
x + y = 6 ……………… (1)
and 3x + y = 8 …………….. (2)
Subtracting (1) and (2),
2x = 2 ⇒ x = 1 ⇒ y = 5
∴ The point P is (1, 5).
Q is the point of intersection of the lines
x + 2y = 10 …………….. (3)
and x + y = 6 ………….. (4)
Subtracting (4) from (3), y = 4 ⇒ x = 2.
So, point Q is (2, 4).
The objective function is Z = 16x + 20y.
At F(0, 8), Z = 16x + 20y = 0 + 160 = 160
At P(1, 5), Z = 16 + 100 = 116
At Q(2, 4), Z = 32 + 80 = 112
At A(10, 0), Z = 160 + 0 = 160
This shows that minimum value of Z is ₹112.
Feasible region is unbounded.
Consider the inequality 16x + 20y < 112. or
4x + 5y < 28
The line 4x + 5y = 28 passes through (7, 0) and (0, \(\frac{28}{5}\).
Also, putting x = 0, y = 0 in 4x + 5y < 28,
we get, 0 < 28, which is true.
∴ 4x + 5y < 28 lies below the line 4x + 5y = 28.
Hence, there is no common point between feasible region and 4x + 5y < 28.
⇒ Minimum value of Z = 112 at x = 2 and y = 4, i.e., least value of the mixture is ₹112, when 2 kg of food X and 4 kg of food Y are mixed.
![]()
Question 4.
A manufacturer makes two types of toys A and B.
Three machines are needed for this purpose and the time (in minutes) required for making each toy on the machines is given below:

Each machine is available for a maximum of 6 hours per day.
If the profit on each toy of type A is ₹7.50 and that on each toy of type B is ₹5,
show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
Solution:
Let x toys of type A and y toys of type B are manufactured. Profits on each toy of type A and type B are ₹7.50 and ₹5 respectively.
∴ We have to maximise Z = 7.5x + 5y.
The constraints are
12x + 6y ≤ 360, 18x ≤ 360, 6x + 9y ≤ 360
i.e., 2x + y ≤ 60, x ≤ 20, 2x + 3y ≤ 120 and also x, y ≥ 0.
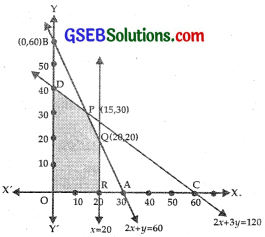
(i) The line 2x + y = 60 passes through A(30, 0) and B(0, 60).
Put x = 0, y = 0 in 2x + y ≤ 60, we get 0 ≤ 60, which is true.
⇒ 2x + y ≤ 60 lies on and below AB.
(ii) x ≤ 20 is the region lies on x = 20 and to the left of it.
(iii) 2x + 3y = 120 passes through C(60, 0) and D(0, 40).
Putting x = 0, y = 0, in 2x + 3y ≤ 120, we get 0 ≤ 120, which is true.
∴ 2x + 3y ≤ 120 lies on and below CD.
(iv) x ≥ 0 lies on and to the right of y-axis.
(v) y ≥ 0 lies on and above x-axis.
The shaded area DPQRO is the feasible region.
P is the point of intersection of the lines
2x + y = 60 ……………… (1)
and 2x + 3 y = 120 ……………… (2)
Subtracting (1) from (2),
2x + y = 60 ⇒ y = 30
∴ 2x = 60 – 30 = 30, x = 15
∴ The point P is (15, 30).
Q is the point of intersection of x = 20 and 2x + y = 60 ⇒ y = 20.
∴ Q is (20, 20).
Now, Z = 7.5x + 5y
At P(15, 30), Z = 7.5 × 15 + 5 × 30
= 112.5 + 150
= 262.5
At Q(20, 20), Z = 7.5 × 20 + 5 × 20
= 150 + 100
= 250
At D(0, 40), Z = 0 + 5 × 40
= 200
At R(20, 0), Z = 7.5 × 20 + 0
= 150
Thus, to have maximum profit ₹262.50, 15 toys of type A and 30 toys of type B should be manufactured.
![]()
Question 5.
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket.
The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by executive class.
Determine how many tickets of each type must be sold in order to maximise profit for the airline? What is the maximum profit?
Solution:
Let the executive class air tickets and economy class tickets sold be x and y.
Now, as the seating capacity of the aeroplane is 200,
so x + y ≤ 200.
As 20 tickets for executive class are to be reserved, so we have: x ≥ 20.
And as the number of tickets of economy class should be at least 4 times that of executive class y ≥ 4x.
Profit Z on sale of x tickets of 1st class and y tickets of economy class is given by Z = 1000x + 600y.
∴ Our L.P.P. is to maximise Z = 1000x + 600y subject to constraints x + y ≤ 200, x ≥ 20, y ≥ 4x and x, y ≥ 0.
Plot lines x + y = 200, x = 20 and y = 4x on a graph paper.
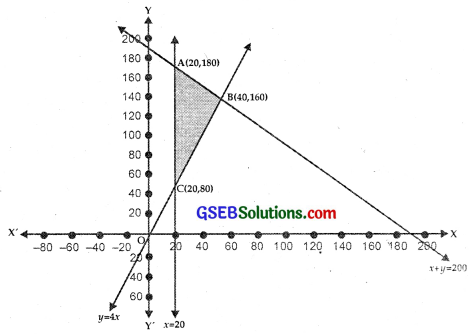
The region satisfying the inequalities x + y < 200, x > 20 and y > 4x is
ABC and is shown shaded in the figure.
Now, objective function is:
Z = 1000x + 600y
At A(20, 180), Z = 1000 × 20 + 600 × 180
= 20000 + 108000 = 128000
At B(40, 160),
Z = 1000 × 40 + 600 × 160
= 40000 + 96000 = 136000
At C(20, 80), Z = 1000 × 20 + 600 × 80
⇒ 20000 + 48000
= 68000
⇒ Z is maximum, when
x = 40 and y = 160.
⇒ 40 tickets of executive class and 160 tickets of economy class should be sold to get the maximum profit of ₹136000.
![]()
Question 6.
Two godowns A and B have grains capacity of 100 quintals and 50 quintals respectively.
They supply to 3 ration shops D, E and F whose requirements are 60, 50 and 40 quintals respectively.
The cost of transportation per quintal from the godowns to the shops are given in the following table:
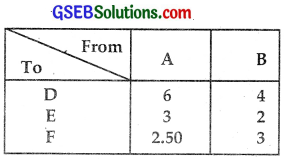
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
Solution:
Let x quintals of grains are transported from godown A to ration shop D and y quintals of grains are transported from godown A to ration shop E.
Now, the grains transported from godown A to shop F will be 100 – (x + y) quintals. Since capacity of godown A is 100 quintals.
Thus, we have x ≥ 0, y ≥ 0 and 100 – (x + y) ≥ 0, i.e., x + y ≤ 100.
As requirement of grains at shop D is of 60 quintals, (60 – x) quintals of grains be transported from godown B to D.
Similarly, (50 – y) quintals and 40 – [100 – (x + y)] should be transported from godown B to shop E and F, respectively.
∴ (60 – x) ≥ 0, i.e., x ≤ 60, (50 – y) ≥ 0
Z = 6x + 3y + 2.50(100 – x – y) + 4(60 – x) + 2(50 – y) + 3{40 – [100 – (x + y)]}
= 6x + 3y + 150 – 2.50x – 2.50y + 240 – 4x + 100 – 2y + 120 – 300 + 3x + 3y
= 2.50x + 1.5y + 410
So, our L.P.P. is to minimise
Z = 2.5x + 1.5y + 410
subject to constraints
x ≤ 60, y ≤ 50, x + y ≥ 60, x + y ≤ 100, x, y ≥ 0.
Plot the graphs of equations x = 60, y = 50, x + y = – 60, x + y = 100 on a graph paper.
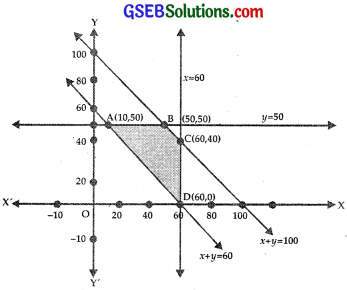
The region ABCD shows shaded area in the figure which satisfies the inequalities x ≤ 60, y ≤ 50, x + y ≥ 60, x + y ≤ 100 and x, y ≥ 0.
We calculate values of Z at points A, B, C and D which are the corner points of the region ABCD.
At A(10, 50), Z = 2.5x + 1.5y + 410
= 2.5 × 10 + 1.5 × 50 + 410
= 25 + 75 + 410 = 510
At B(50, 50), Z = 2.5 × 50 + 1.5 × 50 + 410
= 125 + 75 + 410 = 510
At C(60, 40), Z = 2.5 × 60 + 1.5 × 40 + 410
= 150 + 60 + 410 = 620
At D(60, 0), Z = 2.5 × 60 + 0 + 410
= 150 + 410 = 560
Thus, Z is minimum, i.e., ₹510 at A, i.e., when x = 10, and y = 50.
Supply table is given below, when the transportation charges are least.
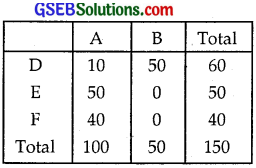
![]()
Question 7.
An oil company has two depots A and B with capacities of 7000L and 4000L respectively.
The company is to supply oil to three petrol pumps D, E and F whose requirements are 4500L, 3000L and 3500L respectively.
The distances (in km) between the depots and the petrol pumps are given in the following table:
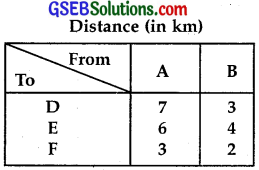
Assuming that the transportation cost of 10 litres of oil is ₹1 per km,
how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?
Solution:
Let x litres oil is supplied from depot A to petrol pump D and y litres of oil is supplied from depot A to petrol pump E.
Then, 7000 – (x + y) litres of oil will be supplied from depot A to petrol pump F.
So, we have x ≥ 0, y ≥ 0 and 7000 – (x + y) ≥ 0, i.e., x + y ≤ 7000.
Now, as requirements of oil at petrol pumps D, E and F are 4500L, 3000L and 3500L, so quantity of oil transported from depot B to petrol pumps D, E and F are (4500 – x), (3000 – y) and 3500 – [7000 – (x + y)] litres, respectively.
i.e. 4500 – x ≥ 0 ⇒ x < 4500,
3000 – y ≥ 0 ⇒ y < 3000
Also, 3500 – [7000 – (x + y)] ≥ 0 (x + y) ≥ 3500.
The cost of transportation per km for 10 litres oil is ₹1.
∴ The cost of transportation per km per litre = ₹\(\frac{1}{10}\) = ₹0.1
⇒ The cost of transportation,
Z = 0.7x + 0.6y + 0.317000 – (x + y)] + 0.3(4500 – x) + 0.4(3000 – y) + 0.2[(x + y) – 3500]
= 0.3x + 0.1y + 3950
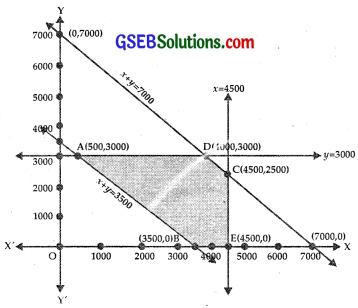
The feasible area is ABECD.
Now the points A, B, E, C, D are:
A(500, 3000), B(3500, 0), E(4500, 0), C(4500, 2500) D(4000, 3000)
Now, Z = 0.3x + 0.1y + 3950
At A(500, 3000), Z = 0.3 × 500 + 0.1 × 3000 + 3950 = 4400
At B(3500, 0), Z = 0.3 × 3500 + 0 + 3950 = 5000
At E(4500, 0), Z = 0.3 × 4500 + 0 + 3950 = 5300
At C(4500, 2500), Z = 0.3 × 4500 + 0.1 × 2500 + 3950 = 5550
At D(4000, 3000), Z = 0.3 × 4000 + 0.1 × 3000 + 3950 = 5450
Minimum transport charges are ₹4400 at A(500, 3000),
when x = 500 and y = 3000.
Thus, 500 litres, 3000 litres and 3300 litres of oil should be transported from depot A to petrol pumps D, E and F respectively and 4000 litres, 0 litre and 0 litre of oil be transported from depot B.
to petrol pumps D, E and F with minimum cost of transportation of ₹4400.
![]()
Question 8.
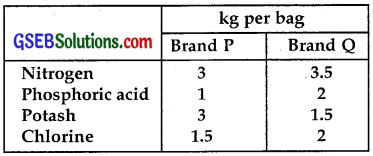
A fruit grower an use two types of fertilisers in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash and chlorine in a bag of each brand are given in the table.
Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower want to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
Solution:
Let x bags of brand P and y bags of brand Q are needed to minimise nitrogen contents.
∴ Objective function is to minimise Z = 3x + 3.5y.
At least 240 kg of phosphoric acid is required.
∴ x + 2y ≥ 240
At least 270 kg of potash is needed.
∴ 3x + 1.5y ≥ 270
At most 310 kg of chlorine is required.
∴ 1.5x + 2y ≤ 310
Thus, objective function is Z = 3x + 3.5y.
Constraints are x + 2y ≥ 240, 3x + 1.5y ≥ 270, 1.5x + 2y ≤ 310, x, y ≥ 0.
(i) The line x + 2y = 240 passes through the points A(240, 0) andB(0, 120).
Putting x = 0, y = 0 in x + 2y ≥ 240, we get
0 ≥ 240, which is not true.
⇒ Region x + 2y ≥ 240 lies on and above AB.
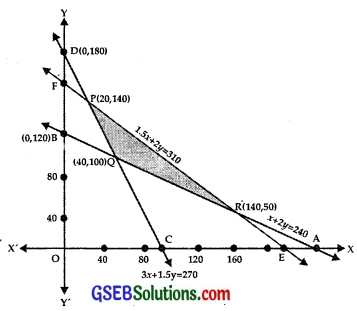
(ii) The line 3x + 1.5y ≥ 270 passes through the points C(90, 0) and D(0, 180).
Putting x = 0, y = 0 in 3x + 1.5y ≥ 270, we get 0 ≥ 270, which is not true.
⇒ Region 3x + 1.5y ≥ 270 lies on CD and above it.
(iii) 1.5x + 2y ≤ 310 passes through the points E(\(\frac{620}{3}\), 0) and F(0, 155).
Putting x = 0, y = 0 in 1.5x + 2y ≤ 310, we get 0 ≤ 310, which is true.
⇒ Region 1.5x + 2y ≤ 310 lies on and below EF.
(iv) x ≥ 0 lies on and to the right of y-axis.
(v) y ≥ 0 lies on and above the x-axis.
The shaded area PQR represents the feasible region.
Now, P is the point of intersection of the lines
3x + 1.5y = 270 ………………… (1)
and 1.5x + 2y = 310 ……………… (2)
Multiplying (2) by 2 and subtracting (1) from it,
2.5y = 620 – 270 = 350
∴ y = \(\frac{350}{5}\) × 2 = 70 × 2 = 140.
From (2), 1.5x = 310 – 2y = 310 – 2 × 140.
= 310 – 280 = 30.
∴ x = \(\frac{30}{3}\) × 2 = 20.
∴ The point P is (20, 140).
Q is the point of intersection of the lines
x + 2y = 240 …………….. (3)
and 3x + 1.5y = 270 ……………. (4)
Multiplying (3) by 3 and subtracting (4) from it,
4.5y = 720 – 270 = 450
⇒ y = \(\frac{450}{9}\) × 2 = 50 × 2 = 100.
From (3), x = 240 – 2y = 240 – 200 = 40.
∴ Point Q is (40, 100).
R is the point of intersection of the lines
x + 2y = 240 …………….. (5)
and 1.5x + 2y = 310 ……………… (6)
Subtracting (5) from (6), we get
0.5x = 70 ⇒ x = 140.
From (5), y = \(\frac{1}{2}\)(240 – 140) = 50.
∴ The point R is (140, 50).
Now, Z = 3x + 3.5y
At P(20, 140), Z = 3x + 3.5y
At Q(40, 100), Z = 60 + 490 = 550
At R(140, 50), Z = 420 + 175 = 595
⇒ Z is the minimum, when x = 40, y = 100.
Minimum amount of nitrogen to be added is 470 kg.
![]()
Question 9.
Refer to question 8 above. If the grower wants to maximise the amount of nitrogen added to the garden,
how many bags of each brand should be added? What is the maximum amount of nitrogen added?
Solution:
From Q. No. 8, We have: Z = 3x + 3.5y
Z is the maximum at R(140, 50).
To maximise the amount of nitrogen, 140 bags of brand P and 50 bags of brand Q are required.
Maximum amount of nitrogen required = 595 kg.
![]()
Question 10.
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A.
Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units.
If the company makes profit of ₹12 and ₹16 per doll respectively on dolls A and B, how many of each type should be produced weekly in order to maximise the profit?
Solution:
Let x dolls of type A and y dolls of type B are produced to have the maximum profit.
Company makes profit of ₹12 and ₹16 per doll respectively on dolls A and B.
⇒ Profit Z = 12.x + 16y.
The production level of x + y should not exceed 1200.
⇒ x + y ≤ 1200
The production level of dolls of type A exceeds three times the production of dolls of type B by at most 600.
⇒ x – 3y ≤ 600
Demand for dolls of type B is at most half of that for dolls of type A.
⇒ y ≤ \(\frac{x}{2}\)
Thus, L.P.P. may be stated as:
To maximise
Z = 12x + 16y.
Constraints are x + y ≤ 1200, x – 3y ≤ 600, y ≤ \(\frac{x}{2}\), x, y ≥ 0.
(i) The line x + y = 1200 passes through A(1200, 0) and B(0, 1200)
Putting x = 0, y = 0 in x + y ≤ 1200, we get 0 ≤ 1200, which is true.
⇒ x + y ≤ 1200 lies on and below AB.
(ii) The line x – 3x = 600
passes through C(600, 0), D(0, – 200)
Putting x = 0, y = 0 in x – 3x ≤ 600,
we get 0 ≤ 600, which is true.
⇒ Origin lies in this region.
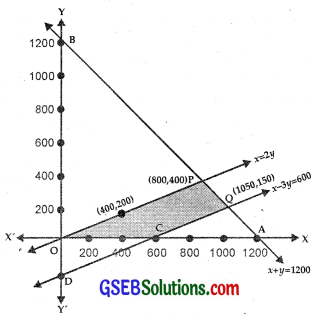
i. e., x – 3y ≤ 600 lies on and above CD.
(iii) y = \(\frac{x}{2}\) passes through (400, 200) and (0, 0).
(iv) x ≥ 0 lies on and to the right of y-axis.
(v) y ≥ 0 lies on and above x-axis.
The shaded area PQCO represents the feasible region.
The point P is the intersection of the lines
x + y = 1200, y = \(\frac{x}{2}\)
Solving, we get the coordinates of P(800, 400).
The point Q is the intersection of the lines
x + y = 1200 …………… (1)
and x – 3y = 600 …………… (2)
Subtracting 4y = 600
⇒ y = 150
⇒ x = 1200 – 150 = 1050
∴ The point Q is (1050, 150).
The point C is (600, 0).
Objective function is Z = 12x + 16y.
At P(800, 400), Z = 9600 + 6400 = 16000
At Q(1050, 150), Z = 12 × 1050 + 16 × 150
= 12600 + 2400 = 15000.
At C(600, 0), Z = 12 × 600 + 0 = 7200
At 0(0, 0), Z = 0
⇒ Z is maximum at P(800, 400). The maximum value of Z is ₹16000.
Thus, to maximise the profit, 800 dolls of type A and 400 dolls of type B should be produced to get a maximum profit of ₹16000.