Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 13 Probability Ex 13.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 13 Probability Ex 13.3
Question 1.
An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned in to the urn. Moreover, 2 additional balls of the colour drawn are put in the um and then a ball is drawn at random.
What is the probability that the second ball is red?
Solution:
Urn contains 5 red and 5 black balls.
(i) Let a red ball is drawn.
Probability of drawing a red ball = \(\frac{5}{10}\) = \(\frac{1}{2}\).
Now, two red balls are added to the urn.
⇒ The urn contains 7 red and 5 black balls.
Probability of drawing a red ball = \(\frac{7}{12}\).
(ii) Let a black ball is drawn at first attempt.
Probability of drawing a black ball = \(\frac{5}{10}\) = \(\frac{1}{2}\).
Next, 2 black balls are added to the urn.
∴ Now, urn contains 5 red and 7 black balls.
∴ Probability of getting a red ball = \(\frac{5}{12}\).
⇒ Probability of drawing a second ball as red
= \(\frac{1}{2}\) × \(\frac{7}{12}\) + \(\frac{1}{2}\) × \(\frac{5}{12}\) = \(\frac{7}{24}\) + \(\frac{5}{24}\)
= \(\frac{7}{24}\) + \(\frac{5}{24}\) = \(\frac{12}{24}\) = \(\frac{1}{2}\).
![]()
Question 2.
A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red.
Find the probability that the ball is drawn from the first bag.
Solution:
Let E1 and E2 be the events of selecting the bags.
∴ Probability of selecting one of the bags = \(\frac{1}{2}\).
i.e; P(E1) = P(E2) = \(\frac{1}{2}\)
I-bag contains 4 red and 4 black balls.
∴ Probability of selecting a red ball from it = \(\frac{4}{8}\) = \(\frac{1}{2}\).
⇒ P(A/E1) = \(\frac{1}{2}\), where A denotes the red ball.
II bag contains 2 red and 6 black balls.
∴ Probability of selecting a red ball from it

Question 3.
Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel).
Previouis year results report that 30% of all students who reside in hostel attain A grade and 20% of day scholar attain A grade in their annual examination.
At the end of the year, one student is chosen at random from the college and he has an A grade. What is the probability that the student is hosteler?
Solution:
Let E1 and E2 denote the event that a student is a hosteler and a day scholar respectively. A denotes that a student is getting grade A.
Probability that a student is a hosteler = 60% = 0.6.
Probability that a student is a day scholar = 40% = 0.4.
Probability that a student gets grade A who is a hosteler
= 30% = 0.3 = P(A/E1).
Probability that, a student gets grade A who is a day scholar
P(A/E2) = 20% = 0.2.
Probability that a hosteler is getting grade A = P(E1/A)

![]()
Question 4.
In answering a question on a multiple choice test, a student knows the answer or guesses. Let \(\frac{3}{4}\) be the probability that he knows the answer and \(\frac{1}{4}\) be the probability that he guesses.
Assuming that a student who guesses at the answer will be correct with probability \(\frac{1}{4}\). What is the probability that a student who knows the answer, given that he answered it correctly?
Solution:
Let the event E1 = Student knows the answer,
and E2 = He guesses the answer.
P(E1) = \(\frac{3}{4}\), P(E2) = \(\frac{1}{4}\).
Let A be the event that answer is correct.
If the student knows the answer.
⇒ Answer is correct.
∴ P(A/E1) = 1
When he guesses the answer
⇒ P(A/E2) = \(\frac{1}{4}\)
∴ Probability that a student knows the answer given that answer is correct is

Question 5.
A laboratory blood test is 99% effective in detecting a certain disease when it is, in fact, present. However, test also yields a false positive result for 0.5% of the healthy person tested (i.e. if a
healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1 percent of the population actually has the disease,
what is the probability that a person has the disease given that his test result is positive?
Solution:
Let E and E’ denote the events that a person has disease and does not have disease respectively.
Further, A = Blood test is positive.
Probability that a person has the disease
P(E) = 0.1% = 0.001.
∴ Probability that a person does not have the disease
= P(E’) = 1 – 0.001
= 0.999.
Probability that a person who has a disease and blood test is positive is
P(A/E) = 99% = 0.99.
Probability that a person does not suffer from disease but has positive blood test = P(A/E’) = 0.005
Now, probability that a person having the disease as well as have positive blood test is P(E/A)

![]()
Question 6.
There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up head 75% of the time and third is an unbiased coin.
One of the three coins is chosen at random and tossed. It shows head. What is the probability that it was the two headed coin?
Solution:
There are three coins. Probability that one of them is selected = \(\frac{1}{3}\)
If E1, E2 and E3 are the events of selecting a coin respectively and A is the event of getting a head.
∴ P(E1) = P(E2) = P(E3) = \(\frac{1}{3}\).
∴ First coin is two headed ⇒ It will always show head
∴ i.e., P(A/E1) = 1.
The second coin is biased and head come up in 75% cases.
⇒ P(A/E2) = 0.75 = \(\frac{3}{4}\).
Third coin is unbiased.
⇒ P(A/E3) = \(\frac{1}{2}\).

Question 7.
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accident by them are 0.01, 0.03 and 0.15 respectively.
One of the insured person meets with an accident. What is the probability that he is a scooter driver?
Solution:
An insurance company insured 2000 scooter & drivers, 4000 car drivers and 6000 truck drivers.
∴ Total number of drivers = 2000 + 4000 + 6000 = 12000
∴ Probability of selecting a scooter driver
= P(E1) = \(\frac{2000}{12000}\) = \(\frac{1}{6}\),
probability of selecting a car driver
= P(E2) = \(\frac{4000}{12000}\) = \(\frac{1}{3}\)
and probability of selecting a truck driver
= P(E3) = \(\frac{6000}{12000}\) = \(\frac{1}{2}\).
Probability of accident of a scooter driver
= P(A/E3) = 0.01,
where A denotes the event of accident.
Probability of accident of car driver = P(A/E2) = 0.03
Probability of accident of truck driver = P(A/E3) = 0.15
Probability the scooter driver has meet an accident

![]()
Question 8.
A factory has two machines A and B. Past record shows that machine A produced 60% of the items of output and machine B produced 40% of the items. Further 2% of the items produced by machine A and 1% produced by machine B were defective.
All the items are put into one stockpile and then one item is chosen at random rom this and is found to be defective.
What is the probability that it was produced by machine B?
Solution:
Let E1 and E2 be the events of production items by machine A and machine B respectively. Let A denotes defective item.
Machine A’s production of items = 60%
∴ Probability of production of items by machine A is
P(E1) = 60% = 0.6
and probability of production of items by machine B is
P(E2) = 40% = 0.4
Also, probability that machine A produced defective item is
P(A/E1) = 2% = 0.02
and probability that machine B produced defective item is
P(A/E2) = 1% = 0.01
Thus, P(E1) = 0.6, P(E2) = 0.4,
P(A/E1) = 0.02 and P(A/E2) = 0.01.
We have to find the probability the defective item selected at random produced from machine B = P(E2/A)

![]()
Question 9.
Two groups are competing for the positions on the board of directors of a corporation. The probabilities that the first and second groups will win are 0.6 and 0.4 respectively.
Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3, if the second group wins.
Find the probability that the new product was introduced by the second group.
Solution:
Let E1 and E2 be the events that I and II group win respectively and A denotes that a new product is introduced.
Now, we have:
Probability that I group wins = P(E1) = 0.6.
Probability that II group wins = P(E2) = 0.4.
Probability that new product was introduced by I group
P(A/E1) = 0.7.
Probability that new product was introduced by II group
P(A/E2) = 0.3.
i.e., P(E1) = 0.6, P(E2) = 0.4,
P(A/E1) = 0.7 and P(A/E2) = 0.3.
Now the probability that new product was introduced by second group is given by

Question 10.
Suppose a girl throws a dice. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin once and notes whether a head or tail is obtained.
If she obtained exactly one head, what is the probability that she threw, 2, 3 or 4 with the dice?
Solution:
When a dice is thrown, there are 6 exhaustive cases.
If she gets 5 or 6, the probability of E1 = \(\frac{2}{6}\) = \(\frac{1}{3}\).
i.e., P(E1) = \(\frac{1}{3}\).
If she gets 1, 2, 3 or 4, the probability of E2 = \(\frac{4}{6}\) = \(\frac{2}{3}\).
i.e., P(E2) = \(\frac{2}{3}\).
When she gets 5 or 6, she throws a coin three times.
The exhaustive cases are 8 viz.
{HHH, HHT, HTH, THH, HTT, THT, TTH, ITT}
One heads may be obtained as {HIT, THT, TTH)
∴ Probability of getting exactly one head = \(\frac{3}{8}\).
If A denotes the event of getting exactly one head, then
P(A/E1) = \(\frac{3}{8}\).
When she gets 1, 2, 3 or 4, she throws a coin once.
The probability of getting one head = \(\frac{1}{2}\).
Probability that she gets exactly one head when she threw 1, 2, 3, or 4 from dice is

![]()
Question 11.
A manufacturer has three machine operators A, B and C. The first operator A produces 1% defective items, whereas the other two operators B and C produce 5% and 7% defective items respectively.
A is on the job for 50% of time, B on the. job for 30% of the time and C is on the job for 20% of the time. If a defective item is produced, what is the probability that it was produced by A?
Solution:
Let E1, E2 and E3 denote the events of time consumed by operators A, B and C respectively.
i.e., P(E1) = 50% = 0.5, P(E2) = 30% = 0.3,
P(E3) = 20% = 0.2.
Let A denotes the event of getting a defective item.
First operator produced 1% defective items.
⇒ P(E/A1) = 0.01.
Second operator produced 5% defective items.
⇒ P(E/A2) = 0.05.
Third operator produced 7% defective items.
⇒ P(E/A3) = 0.07.
Thus, P(E1) = 0.5, P(E2) = 0.3, P(E3) = 0.2,
P(A/E1) = 0.01, PA(E2) = 0.05,
P(A/E2) = 0.07.
Probability that a defective item was produced by operator A is given by

Question 12.
A card from a pack of 52 cards is lost. From the remaining cards of the pack; two cards are drawn and found to be both diamond.
Find the probability of the lost card being a diamond.
Solution:
Let E1 = Event that lost card is a diamond
and E2 = Event that lost card is not a diamond.
There are 13 diamond cards, out of a pack of 52 cards.
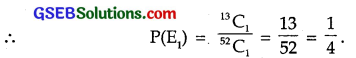
There are 39 cards which are not diamond.
∴ P(E2) = \(\frac{39}{52}\) = \(\frac{3}{4}\).
(i) When one diamond card is lost, 12 diamond cards are left and in total 51 cards are left. Out of 12 cards, 2 may be drawn in 12C2 way.
∴ Probability of getting 2 diamond cards, when one diamond card is lost is
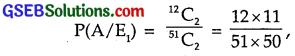
where A denotes the lost card.
When diamond card is not lost, there are 13 diamond cards, the probability of drawing 2 diamond cards is given by

Probability that the lost card is a diamond = P(E1/A)

![]()
Question 13.
Probability that A speaks truth is \(\frac{4}{5}\). A reports that head appears. The probability that actually there was head is:
(A) \(\frac{4}{5}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
Solution:
Let E1 = A speaks truth
and E2 = A does not speak truth.
P(E1) = \(\frac{4}{5}\) (given)
∴ P(E2) = 1 – P(E1) = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\).
A is an event that a head appears.
⇒ P(A/E1) = \(\frac{1}{2}\), when A quotes head.
When A does not speak truth, he says it is a head.
Probability of getting a head
P(A/E2) = \(\frac{1}{2}\)
Probability that actually it is a head = P(E1/A)

∴ Part (A) is the correct answer.
![]()
Question 14.
If A and B are two events such that A ⊂ B and P(B) ≠ 0, then which of the following is true?
(A) P(A/B) = \(\frac{P(B)}{P(A)}\)
(B) P(A/B) < P(A)
(C) P(A/B) ≥ P(A)
(D) None of these
Solution:
A ⊂ B ⇒ A ∩ B = A ⇒ P(A ∩ B) = P(A)
∴ P(A/B) = \(\frac{P(A∩B)}{P(B)}\)
= \(\frac{P(A)}{P(B)}\)
But P(B) ≤ 1
⇒ P(A/B) ≥ P(A).
∴ Part (C) is the correct answer.