GSEB Solutions Class 12 Maths Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise

Question 1.
cos^-1(cos\(\frac { 13π }{ 6 }\))
Solution:
cos^-1(cos\(\frac { 13π }{ 6 }\)) = cos^-1cos(2π + \(\frac { π }{ 6 }\) = cos^-1cos\(\frac { π }{ 6 }\)) = \(\frac { π }{ 6 }\)

Question 2.
tan^-1(tan\(\frac { 7π }{ 6 }\))
Solution:
tan^-1(tan\(\frac { 7π }{ 6 }\)) = tan^-1tan(π + \(\frac { π }{ 6 }\) = tan^-1tan\(\frac { π }{ 6 }\)) = \(\frac { π }{ 6 }\).

Question 3.
sin^-1\(\frac { 3 }{ 5 }\) = tan^-1\(\frac { 24 }{ 7 }\)
Solution:
Let sin^-1\(\frac { 3 }{ 5 }\) = θ

Question 4.
sin^-1\(\frac { 8 }{ 17 }\) + sin^-1\(\frac { 3 }{ 5 }\) = sin^-1\(\frac { 77 }{ 85 }\)
Solution:

Question 5.
cos^-1\(\frac { 4 }{ 5 }\) + cos^-1\(\frac { 12 }{ 13 }\) = cos^-1\(\frac { 33 }{ 65 }\)
Solution:

Question 6.
cos^-1\(\frac { 12 }{ 13 }\) + sin^-1\(\frac { 3 }{ 5 }\) = sin^-1\(\frac { 56 }{ 65 }\)
Solution:

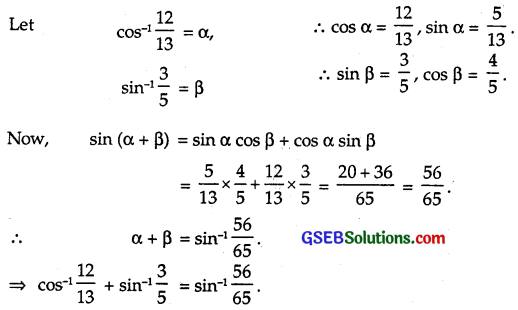
Question 7.
tan^-1\(\frac { 63 }{ 16 }\) = sin^-1\(\frac { 5 }{ 13 }\) + cos^-1\(\frac { 3 }{ 5 }\)
Solution:

Question 8.
tan^-1\(\frac { 1 }{ 5 }\) + tan^-1\(\frac { 1 }{ 7 }\) + tan^-1\(\frac { 1 }{ 3 }\) + tan^-1\(\frac { 1 }{ 8 }\) = \(\frac { π }{ 4 }\)
Solution:

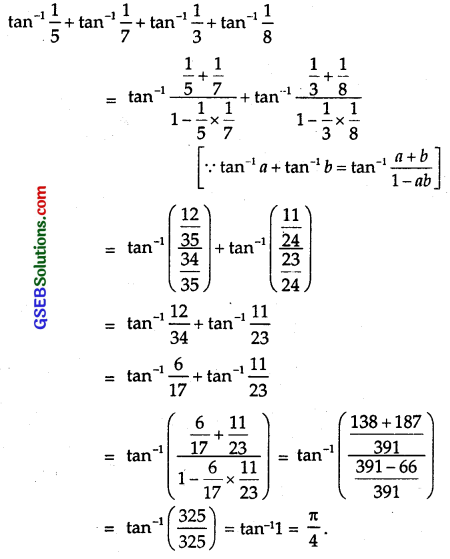
Question 9.
tan^-1\(\sqrt{x}\) = \(\frac { 1 }{ 2 }\)cos^-1\(\frac { 1-x }{ 1+x }\), x ∈ [0, 1]
Solution:
Put x = tan²θ. ∴ θ = tan^-1\(\sqrt{x}\)
R.H.S.
= \(\frac { 1 }{ 2 }\)cos^-1\(\frac { 1-x }{ 1+x }\)
= \(\frac { 1 }{ 2 }\)cos^-1\(\left(\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}\right)\)
= \(\frac { 1 }{ 2 }\)cos^-1(cos2θ) = \(\frac { 1 }{ 2 }\) x 2θ = θ.
= tan^-1\(\sqrt{x}\) = L.H.S
Hence, tan^-1\(\sqrt{x}\) \(\frac { 1 }{ 2 }\)cos^-1\(\frac { 1-x }{ 1+x }\)

Question 10.
cot^-1\(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\) = \(\frac { x }{ 2 }\), x ∈ (0, \(\frac { π }{ 4 }\))
Solution:

Question 11.
tan^-1\(\left(\frac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}\right)\) = \(\frac { π }{ 4 }\) + \(\frac { 1 }{ 2 }\)cos^-1, x ∈ (0, \(\frac { π }{ 4 }\))
Solution:

Question 12.
\(\frac { 9π }{ 8 }\) – \(\frac { 9 }{ 4 }\)sin^-1\(\frac { 1 }{ 3 }\) = \(\frac { 9 }{ 4 }\)sin^-1\(\frac{2 \sqrt{2}}{3}\)
Solution:
\(\frac { 9π }{ 8 }\) – \(\frac { 9 }{ 4 }\)sin^-1\(\frac { 1 }{ 3 }\) = \(\frac { 9 }{ 4 }\)sin^-1\(\frac{2 \sqrt{2}}{3}\)
⇒ \(\frac { 9 }{ 4 }\)(sin^-1\(\frac{2 \sqrt{2}}{3}\) + sin^-1\(\frac { 1 }{ 3 }\)) = \(\frac { 9π }{ 8 }\)

Hence \(\frac { 9π }{ 8 }\) – \(\frac { 9 }{ 4 }\)sin^-1\(\frac { 1 }{ 3 }\) = \(\frac { 9 }{ 4 }\)sin^-1\(\frac{2 \sqrt{2}}{3}\)

Question 13.
2tan^-1(cos x) = tan^-1(cosec x)
Solution:
Now L.H.S
= 2tan^-1(cos x)
= tan^-1\(\left(\frac{2 \cos x}{1-\cos ^{2} x}\right)\)
= tan^-1\(\left(\frac{2 \cos x}{\sin ^{2} x}\right)\)
Putting this value in the given equation, we get
tan^-1\(\left(\frac{2 \cos x}{\sin ^{2} x}\right)\) = tan^-1(2 cosec x)
⇒ \(\frac{2 \cos x}{\sin ^{2} x}\) = 2 cosec x = \(\frac { 2 }{ sin x }\)
⇒ cos x = sin x or tan x = 1
⇒ x = \(\frac { π }{ 4 }\)

Question 14.
tan^-1\(\frac { 1-x }{ 1+x }\) = \(\frac { 1 }{ 2 }\)tan^-1x, x > 0
Solution:

Question 15.
sin tan^-1x, |x| < 1 is equal to
(A) \(\frac{x}{\sqrt{1-x^{2}}}\)
(B) \(\frac{1}{\sqrt{1-x^{2}}}\)
(C) \(\frac{1}{\sqrt{1+x^{2}}}\)
(D) \(\frac{x}{\sqrt{1+x^{2}}}\)
Solution:
Let tan^-1x = α ∴ tan α = x.
So, sin α = \(\frac{x}{\sqrt{1+x^{2}}}\)
or α = sin^-1\(\frac{x}{\sqrt{1+x^{2}}}\)
Now sin tan^-1x = sin α = sin(sin^-1\(\frac{x}{\sqrt{1+x^{2}}}\))
= \(\frac{x}{\sqrt{1+x^{2}}}\)
∴ Part (D) is the correct answer.

Question 16.
If sin^-1(1-x)-2 sin^-1x = \(\frac { π }{ 2 }\), then x is equal to
(A) 0, \(\frac { 1 }{ 2 }\)
(B) 1, \(\frac { 1 }{ 2 }\)
(C) 0
(D) \(\frac { 1 }{ 2 }\)
Solution:
sin^-1(1-x)-2 sin^-1x = \(\frac { π }{ 2 }\)
Putting \(\frac { π }{ 2 }\) = sin^-1(1 – x) + cos^-1(1 – x),
sin^-1(1 – x) – 2 sin^-1 = sin^-1(1 – x) + cos^-1(1 – x)
⇒ – 2 sin^-1x = cos^-1(1 – x)
Let sin^-1x = α. ∴ sin a = α
∴ – 2 sin^-1x = – 2α = cos^-1(1 – x)
or cos 2α = 1 – x [∵ cos (-θ) = cos θ]
∴ 1 – 2sin²α = (1 – x)
Putting sin α = x, we get
1 – 2x² = 1 – x
or 2x² – x = 0
⇒ x(2x – 1) = 0. ∴ x = 0, \(\frac { 1 }{ 2 }\)
But x = \(\frac { 1 }{ 2 }\) does not satisfy the equation. ∴ x = 0.
∴ Part (C) is the correct answer.

Question 17.
tan^-1(\(\frac { x }{ y }\)) tan^-1(\(\frac { x-y }{ x+y }\)) is equal to
(A) \(\frac { π }{ 2 }\)
(B) \(\frac { π }{ 3 }\)
(C) \(\frac { π }{ 4 }\)
(D) \(\frac { -3π }{ 4 }\)
Solution:
tan^-1(\(\frac { x }{ y }\)) tan^-1(\(\frac { x-y }{ x+y }\))
Applying the formula tan^-1a tan^-1b = tan^-1\(\frac { a-b }{ 1+ab }\), we get:
Given expression

∴ Part (C) is the required answer.