Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 3 Matrices Ex 3.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 3 Matrices Ex 3.2
![]()
Question 1.
Let A = \(\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]\), B = \(\left[\begin{array}{ll} 1 & 3 \\ -2 & 5 \end{array}\right]\), C = \(\left[\begin{array}{ll} -2 & 5 \\ 3 & 4 \end{array}\right]\).
Find each of the following:
(i) A + B
(ii) A-B
(iii) 3A-C
(iv) AB
(v) BA
Solution:

Question 2.
Compute the following:
(i) \(\left[\begin{array}{cc} a & b \\ -b & a \end{array}\right]\) + \(\left[\begin{array}{cc} a & b \\ b & a \end{array}\right]\)
(ii) \(\left[\begin{array}{ll} a^{2}+b^{2} & b^{2}+c^{2} \\ a^{2}+c^{2} & a^{2}+b^{2} \end{array}\right]\) + \(\left[\begin{array}{cc} 2 a b & 2 b c \\ -2 a c & -2 a b \end{array}\right]\)
(iii) \(\left[\begin{array}{ccc} -1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5 \end{array}\right]\) + \(\left[\begin{array}{ccc} 12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4 \end{array}\right]\)
(iv) \(\left[\begin{array}{cc} \cos ^{2} x & \sin ^{2} x \\ \sin ^{2} x & \cos ^{2} x \end{array}\right]\) + \(\left[\begin{array}{cc} \sin ^{2} x & \cos ^{2} x \\ \cos ^{2} x & \sin ^{2} x \end{array}\right]\)
Solution:

![]()
Question 3.
Compute the indicated products:
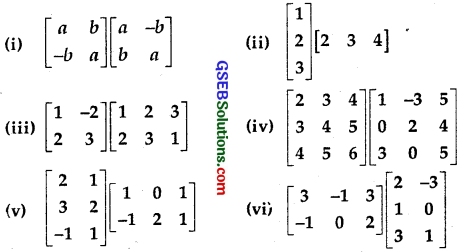
Solution:

Question 4.
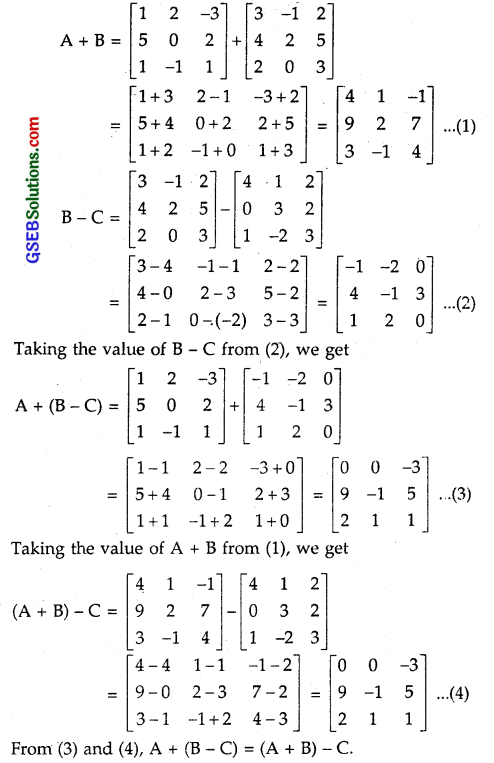
If A = \(\left[\begin{array}{ccc} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{array}\right]\) B = \(\left[\begin{array}{ccc} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{array}\right]\) and C = \(\left[\begin{array}{ccc} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{array}\right]\), then compute (A + B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
Solution:
![]()
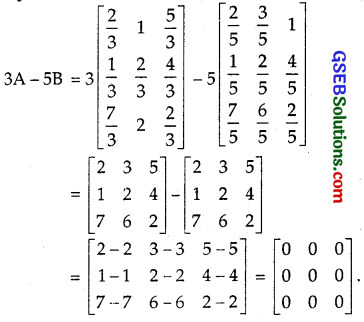
Question 5.
A = \(\left[\begin{array}{ccc} \frac{2}{3} & 1 & \frac{5}{3} \\ \frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\ \frac{7}{3} & 2 & \frac{2}{3} \end{array}\right]\) and B = \(\left[\begin{array}{ccc} \frac{2}{5} & \frac{3}{5} & 1 \\ \frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\ \frac{7}{5} & \frac{6}{5} & \frac{2}{5} \end{array}\right]\), then compute 3A – 5B.
Solution:
Question 6.
Simplify : cos θ \(\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]\) + sin θ\(\left[\begin{array}{cc} \sin \theta & -\cos \theta \\ \cos \theta & \sin \theta \end{array}\right]\)
Solution:
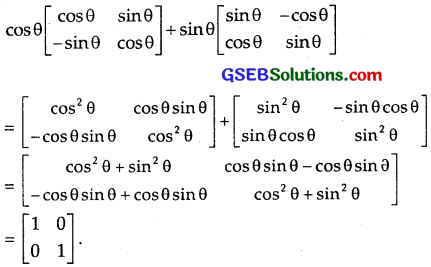
Question 7.
Find X and Y, if
(i) X + Y =\(\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right]\) and X – Y = \(\left[\begin{array}{ll} 3 & 0 \\ 0 & 3 \end{array}\right]\)
(ii) 2X + 3Y = \(\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right]\) and 3X + 2Y = \(\left[\begin{array}{cc} 2 & -2 \\ -1 & 5 \end{array}\right]\)
Solution:

Question 8.
Find X, if Y = \(\left[\begin{array}{ll} 3 & 2 \\ 1 & 4 \end{array}\right]\) and 2X + Y = \(\left[\begin{array}{ll} 1 & 0 \\ -3 & 2 \end{array}\right]\).
Solution:
2X + Y = \(\left[\begin{array}{ll} 1 & 0 \\ -3 & 2 \end{array}\right]\)
∴ 2X = \(\left[\begin{array}{ll} 1 & 0 \\ -3 & 2 \end{array}\right]\) – Y = \(\left[\begin{array}{ll} 1 & 0 \\ -3 & 2 \end{array}\right]\) – \(\left[\begin{array}{ll} 3 & 2 \\ 1 & 4 \end{array}\right]\) = \(\left[\begin{array}{ll} -2 & -2 \\ -4 & -2 \end{array}\right]\)
∴ X = \(\left[\begin{array}{ll} -1 & -1 \\ -2 & -1 \end{array}\right]\).
![]()
Question 9.
Find x and y, if 2\(\left[\begin{array}{ll} 1 & 3 \\ 0 & x \end{array}\right]\) + \(\left[\begin{array}{ll} y & 0 \\ 1 & 2 \end{array}\right]\) = \(\left[\begin{array}{ll} 5 & 6 \\ 1 & 8 \end{array}\right]\).
Solution:

Equating the corresponding elements, we get:
2 + y = 5. ∴ y = 5 – 2 = 3.
2x + 2 = 8. ∴ 2x = 8 – 2 = 6. or x = 3
Hence, x = 3 and y = 3.
Question 10.
Solve the equation for x, y, z and t,
if, 2\(\left[\begin{array}{ll} x & z \\ y & t \end{array}\right]\)+3\(\left[\begin{array}{ll} 1 & -1 \\ 0 & 2 \end{array}\right]\) = 3\(\left[\begin{array}{ll} 3 & 5 \\ 4 & 6 \end{array}\right]\).
Solution:
2\(\left[\begin{array}{ll} x & z \\ y & t \end{array}\right]\)+3\(\left[\begin{array}{ll} 1 & -1 \\ 0 & 2 \end{array}\right]\) = 3\(\left[\begin{array}{ll} 3 & 5 \\ 4 & 6 \end{array}\right]\)
or \(\left[\begin{array}{ll} 2x & 2z \\ 2y & 2t \end{array}\right]\)+\(\left[\begin{array}{ll} 3 & -3 \\ 0 & 6 \end{array}\right]\) = \(\left[\begin{array}{ll} 9 & 15 \\ 12 & 18 \end{array}\right]\)
or \(\left[\begin{array}{cc} 2 x+3 & 2 z-3 \\ 2 y & 2 t+6 \end{array}\right]\) = \(\left[\begin{array}{cc} 9 & 15 \\ 12 & 18 \end{array}\right]\).
Equating corresponding elements, we get:
2x + 3 = 9 or 2x = 9 – 3 = 6. ∴ x = 3.
2y = 12 ∴ y = 6.
2z – 3 = 15 or 2z – 15 + 3 = 18 ∴ z = 9.
2t + 6 = 18 or 2t = 18 – 6 = 12 ∴ t = 6.
Thus, x = 3, y = 6, z = 9 and t = 6.
![]()
Question 11.
If x\(\left[\begin{array}{l} 2 \\ 3 \end{array}\right]\) + y\(\left[\begin{array}{l} -1 \\ 1 \end{array}\right]\) = \(\left[\begin{array}{l} 10 \\ 5 \end{array}\right]\), then find the values of x and y.
Solution:
x\(\left[\begin{array}{l} 2 \\ 3 \end{array}\right]\) + y\(\left[\begin{array}{l} -1 \\ 1 \end{array}\right]\) = \(\left[\begin{array}{l} 10 \\ 5 \end{array}\right]\).
or \(\left[\begin{array}{l} 2x \\ 3x \end{array}\right]\) + \(\left[\begin{array}{l} -y \\ y \end{array}\right]\) = \(\left[\begin{array}{l} 10 \\ 5 \end{array}\right]\)
or \(\left[\begin{array}{l} 2 x-y \\ 3 x+y \end{array}\right]\) = \(\left[\begin{array}{l} 10 \\ 5 \end{array}\right]\)
Equating the corresponding elements, we get:
2x – y = 10 … (1)
3x + y = 5 … (2)
Adding (1) and (2), we get
5x – 15 ⇒ x = \(\frac { 15 }{ 5 }\) = 3.
Putting value of x in (1), we get
2x – y = 2 x 3 – y = 10
∴ y = 6 – 10 = – 4.
Hence, x = 3, and y = – 4.
Question 12.
Given 3 \(\left[\begin{array}{ll} x & y \\ z & w \end{array}\right]\) = \(\left[\begin{array}{ll} x & 6 \\ -1 & 2w \end{array}\right]\) + \(\left[\begin{array}{ll} 4 & x+y \\ z+w & 3 \end{array}\right]\), find the values of x, y, z and w.
Solution:

Question 13.
If F(x) = \(\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]\), then show that
F(x)F(y) = F(x + y).
Solution:
L.H.S = F(x)F(y)

= F(x+y) = R.H.S
Hence, F(x)F(y) = F(x+y)
![]()
Question 14.
Show that:
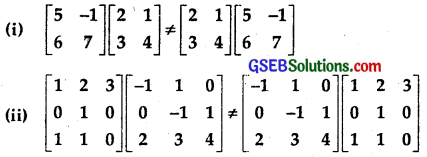
Solution:

Question 15.
Find A² – 5A + 6I, if A = \(\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]\)
Solution:

Question 16.
If A = \(\left[\begin{array}{ccc} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right]\), prove that A³ – 6A² + 7A + 2I = 0.
Solution:

Question 17.
If A = \(\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]\) and I = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\), then find k such that A² = kA – 2I.
Solution:

Question 18.
If A = \(\left[\begin{array}{rr} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]\) and I is the identity matrix of order 2, show that I + A = (I – A)\(\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\).
Solution:
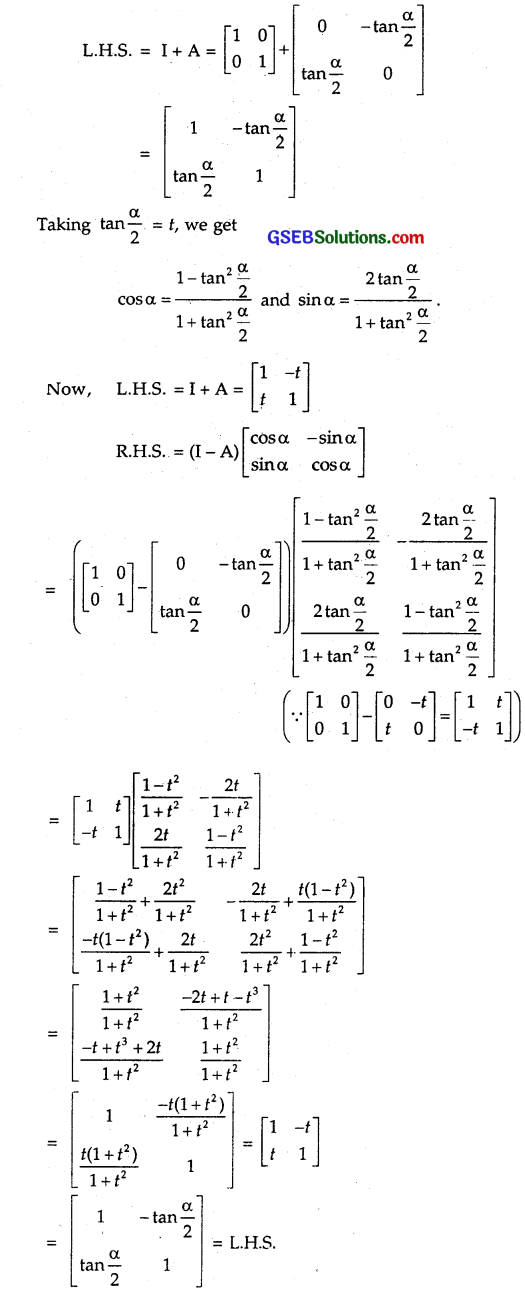
Hence, the result.
![]()
Question 19.
A trust has ₹ 30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year and second bond pays 7% interest per year. Using matrix multiplication, determine how to divide ₹ 30,000 among the two types of bond, if the trust fund obtains an annual total interest of :
(a) ₹ 1,800
(b) ₹ 2,000.
Solution:
Let ₹ 30,000 be divided into two parts.
viz. ₹ x and ₹ (30000 – x).
Let it be represented by 1 x 2 matrix [x (30000 – x)]
Rate of interest is 0.05 and 0.07 per rupee. Let it be denoted a matrix R of order 2 x 1 as shown below :

Thus, the two parts are ₹ 15000 each.
(b) Here, the total interest is ₹ 2000.
Proceeding as above, we have :

Question 20.
The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books and 10 dozen economics books. Their selling prices are ₹ 80, ₹ 60, ₹ 40 each respectively. Find the total amount the bookshop will receive from selling all the books, using matrix algebra.
Solution:
Let the number of books be represented by matrix A of order 1 x 3 as shown below :
A = [10 dozen 8 dozen 10 dozen]
= [120 96 120].
The cost of each book of chemistry, physics and economics are ₹ 80, ₹ 60 and ₹ 40 respectively. They are represented by the matrix R of order 3 x 1, i.e.,
R = \(\left[\begin{array}{l} 80 \\ 60 \\ 40 \end{array}\right]\)
Total amount (in ₹) received by selling all the books is given
AR = [120 96 120] \(\left[\begin{array}{l} 80 \\ 60 \\ 40 \end{array}\right]\)
= [120 x 80 + 96 x 60 + 120 x 40]
= [9600 + 5760 + 4800]
= [20160].
∴ Total amount received = ₹ 20160.
Assume that X, Y, Z, W and P are matrices of order 2 x n, 3 x k, 2 x p, n x 3 and p x k respectively. Now answer the following questions 21 and 22:
![]()
Question 21.
The restriction on n, k and p so that PY = WY will be defined are
(A) k = 3, p = n
(B) k is arbitrary, p = 2
(C) p is arbitrary, k = 3
(D) k = 2, p = 3
Solution:
The order of matrix P is p x k
and the order of matrix Y is 3 x k.
PY is defined, when
No. of columns in P = No. of rows in Y.
⇒ k = 3
∴ The order of PY is p x 3.
Now, the order of W is n x 3.
The order of Y is 3 x k.
WY is defined, when
No. of columns in W = No. of rows in Y = 3.
So, WY is defined.
The order of WY = n x 3. .
Matrix PY + WY is defined when PY and WY are of the same order.
But they are of the order p x 3 and nx 3 respectively.
⇒ PY + WY is defined when p = n.
Hence, PY + WY is defined when k = 3 and p = n.
∴ Part (A) is the correct answer.
Question 22.
If n = p, then the order of the matrix 7X – 5Z is
(A) p x 2
(B) 2 x n
(C) n x 3
(D) p x n
Solution:
The order of matrix X is 2 x n.
The order of matrix Z is 2 x p.
7X – 5Z is defined when X and Z are of the same order.
⇒ n-p (given)
Thus, the order of Z is also 2 x n.
Hence, order of 7X – 5Z is 2 x n.
∴ Part (B) is the correct answer.
![]()