Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 3 Matrices Ex 3.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 3 Matrices Ex 3.3
![]()
Question 1.
Find the transpose of each of the following matrices:
(i) \(\left[\begin{array}{c} 5 \\ 1 \\ \hline 2 \\ -1 \end{array}\right]\)
(ii) \(\left[\begin{array}{cc} 1 & -1 \\ 2 & 3 \end{array}\right]\)
(iii) \(\left[\begin{array}{ccc} -1 & 5 & 6 \\ \sqrt{3} & 5 & 6 \\ 2 & 3 & -1 \end{array}\right]\)
Solution:
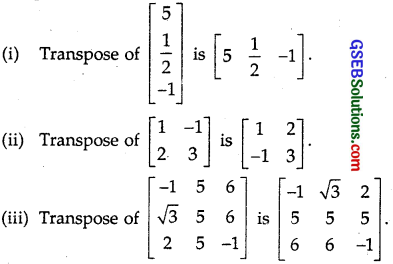
Question 2.
If A = \(\left[\begin{array}{ccc}
-1 & 2 & 3 \\
5 & 7 & 9 \\
-2 & 1 & 1
\end{array}\right]\) + B = \(\left[\begin{array}{ccc}
-4 & 1 & -5 \\
1 & 2 & 0 \\
1 & 3 & 1
\end{array}\right]\), then verify that
(i) (A+B)’ = A’ + B’
(ii) (A-B)’ = A’ – B’
Solution:

Question 3.
If A’ = \(\left[\begin{array}{cc}
3 & 4 \\
-1 & 2 \\
0 & 1
\end{array}\right]\) + B = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]\), then verify that
(i) (A+B)’ = A’ + B’
(ii) (A-B)’ = A’ – B’
Solution:

![]()
Question 4.
If A’ = \(\left[\begin{array}{cc}
-2 & 3 \\
1 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-1 & 0 \\
1 & 2
\end{array}\right]\), then find (A + 2B’)
Solution:
A’ = \(\left[\begin{array}{cc}
-2 & 3 \\
1 & 2
\end{array}\right]\). ∴ A = \(\left[\begin{array}{cc}
-2 & 1 \\
3 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
-1 & 0 \\
1 & 2
\end{array}\right]\).
∴ A + 2B = \(\left[\begin{array}{cc}
-2 & 1 \\
3 & 2
\end{array}\right]\) + 2\(\left[\begin{array}{cc}
-1 & 0 \\
1 & 2
\end{array}\right]\)
= \(\left[\begin{array}{cc} -2 & 1 \\ 3 & 2 \end{array}\right]\) + \(\left[\begin{array}{cc} -2 & 0 \\ 2 & 4 \end{array}\right]\) = \(\left[\begin{array}{cc} -2-2 & 1+0\\ 3+2 & 2+4 \end{array}\right]\)
= \(\left[\begin{array}{cc} -4 & 1 \\ 5 & 6 \end{array}\right]\)
∴(A + 2B)’ = \(\left[\begin{array}{cc} -4 & 1 \\ 5 & 6 \end{array}\right]\) = \(\left[\begin{array}{cc} -4 & 5 \\ 1 & 6 \end{array}\right]\).
![]()
Question 5.
(i) A = \(\left[\begin{array}{c}
1 \\
-4 \\
3
\end{array}\right]\), B = \(\left[\begin{array}{lll}
-1 & 2 & 1
\end{array}\right]\)
(ii) A = \(\left[\begin{array}{c}
0 \\
1 \\
2
\end{array}\right]\), B = \(\left[\begin{array}{lll}
1 & 5 & 7
\end{array}\right]\)
Solution:

Question 6.
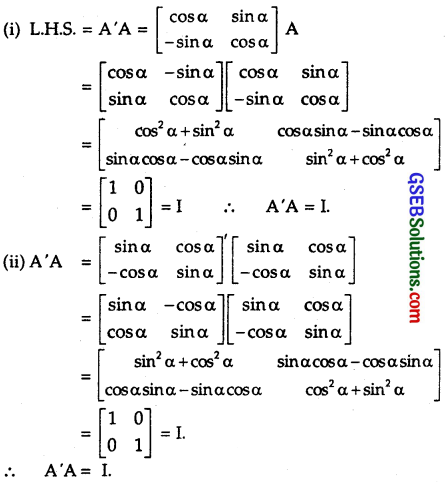
If (i) A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), then verify that A’A = I.
(ii) \(\left[\begin{array}{cc}
\sin \alpha & \cos \alpha \\
-\cos \alpha & \sin \alpha
\end{array}\right]\), then verify that A’A = I.
Solution:
![]()
Question 7.
(i) Show that the matrix A = \(\left[\begin{array}{ccc} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{array}\right]\) is a symmetric matrix.
(ii) Show that the matrix A = \(\left[\begin{array}{ccc} 0 & 1 & -1 \\ -1 & 0 & 1 \\ 1 & -1 & 0 \end{array}\right]\) is a skew – symmetric matrix.
Solution:
(i) For a symmetric matrix a = aij.
Now, A = \(\left[\begin{array}{ccc} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{array}\right]\)
a21 = – 1 = a12, a31 = 5 = a13
a32 = 1 = a23 a11, a22, a33 are 1, 2, 3 respectively.
Hence, aij = aji
∴ A is a symmetric matrix.
Alternatively:
A’ = \(\left[\begin{array}{ccc} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{array}\right]\)‘ = \(\left[\begin{array}{ccc} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{array}\right]\) = A.
∴ A’ = A ⇒ A is a symmetric matrix.
(ii) For a skew symmetric matrix

Question 8.
For a matrix A = \(\left[\begin{array}{ll} 1 & 5 \\ 6 & 7 \end{array}\right]\), verify that
(i) (A + A) is a symmetric matrix.
(ii) (A – A) is a skew symmetric matrix.
Solution:
(i) A = \(\left[\begin{array}{ll} 1 & 5 \\ 6 & 7 \end{array}\right]\) ∴ A’ = \(\left[\begin{array}{ll} 1 & 5 \\ 6 & 7 \end{array}\right]\)
∴ A + A’ = \(\left[\begin{array}{ll} 1+1 & 5+6 \\ 6+5 & 7+7 \end{array}\right]\) = \(\left[\begin{array}{ll} 2 & 11 \\ 11 & 14 \end{array}\right]\)
Here, a21 = 11 = a12
∴ A + A’ is a symmetric matrix.
(i) A – A’ = \(\left[\begin{array}{ll} 1 & 5 \\ 6 & 7 \end{array}\right]\) – \(\left[\begin{array}{ll} 1 & 6 \\ 5 & 7 \end{array}\right]\)
= \(\left[\begin{array}{ll} 1-1 & 5-6 \\ 6-5 & 7-7 \end{array}\right]\) = \(\left[\begin{array}{ll} 0 & -1 \\ 1 & 0 \end{array}\right]\).
Here, a21 = 1, a12 = – 1 or – a12 = 1.
∴ a21 = – a12 a11 = a22 = 0
∴ A – A’ is a symmetric matrix.
Question 9.
Find \(\frac { 1 }{ 2 }\)(A +A) and \(\frac { 1 }{ 2 }\)(A-A), when A = \(\left[\begin{array}{ccc} 0 & a & b \\ -a & 0 & c \\ -b & -c & 0 \end{array}\right]\).
Solution:

![]()
Question 10.
Express the following matrices as the sum of a symmetric and a skew symmetric matrix.
(i) \(\left[\begin{array}{ll} 3 & 5 \\ 1 & -1 \end{array}\right]\)
(ii) \(\left[\begin{array}{ccc} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3 \end{array}\right]\)
(iii) \(\left[\begin{array}{ccc} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2 \end{array}\right]\)
(iv) \(\left[\begin{array}{ll} 1 & 5 \\ -1 & 2 \end{array}\right]\)
Solution:

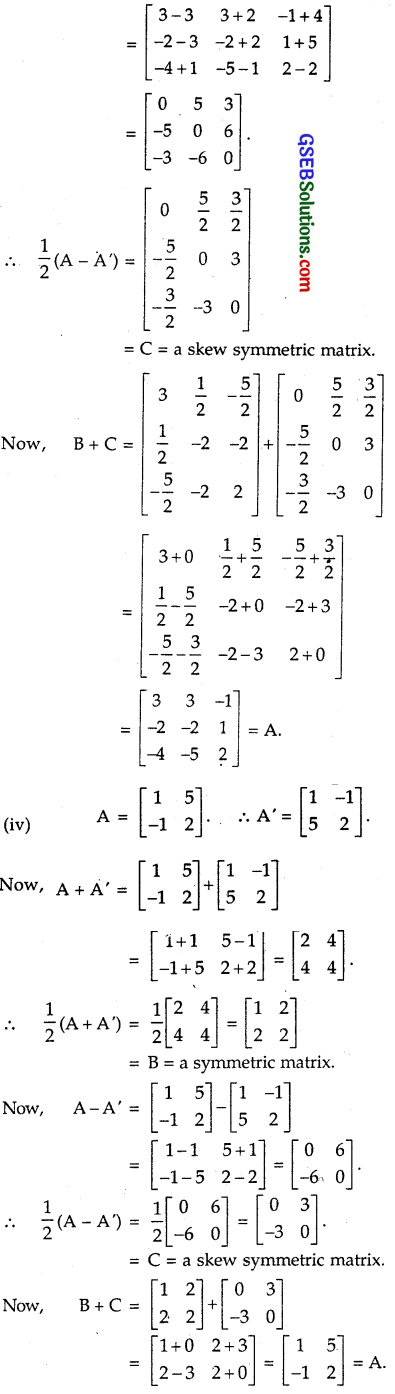
Choose the correct answer in the following questions:
Question 11.
If A and B are symmetric matrices of the same order, then AB – BA is a _____.
(A) Skew symmetric matrix
(B) Symmetric matrix
(C) Zero matrix
(D) Identity matrix
Solution:
A and B are symmetric matrices.
So, A’ = A and B’ = B.
Now, (AB – BA)’ = (AB)’ – (BA)’ = B’A’ – A’B’
= BA – AB [∵ B’ = B, A’ = A]
⇒ AB – BA is a skew symmetric matrix.
∴ Part (A) is the correct answer.
![]()
Question 12.
If A = \(\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\) then A + A’= I, if the value of α is
(A) \(\frac { π }{ 2 }\)
(B) \(\frac { π }{ 3 }\)
(C) π
(D) \(\frac { 3π }{ 2 }\)
Solution:
A = \(\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\) ⇒ A’ = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\)
∴ A + A’ = \(\left[\begin{array}{cc} \cos \alpha+\cos \alpha & -\sin \alpha+\sin \alpha \\ \sin \alpha-\sin \alpha & \cos \alpha+\cos \alpha \end{array}\right]\)
= \(\left[\begin{array}{cc} 2 \cos \alpha & 0 \\ 0 & 2 \cos \alpha \end{array}\right]\) = \(\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\)
2 cos α = 1 ⇒ cos α = \(\frac { 1 }{ 2 }\)
α = \(\frac { π }{ 3 }\)
∴ Part (B) is the correct answer.