Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 3 Matrices Miscellaneous Exercise Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 3 Matrices Miscellaneous Exercise
![]()
Question 1.
Let A = \(\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right]\). Show that (aI + bA)n + nan-1bA, where I is the identity matrix of order n ∈ N
Solution:

Apply Principle of Mathmatical Induction.
Put P(n) : \(\left[\begin{array}{ll} a & b \\ 0 & a \end{array}\right]\)n = \(\left[\begin{array}{cc} a^{n} & n a^{n-1} b \\ 0 & a^{n} \end{array}\right]\).
For n = 1, P(1) : \(\left[\begin{array}{ll} a & b \\ 0 & a \end{array}\right]\) = \(\left[\begin{array}{ll} a & b \\ 0 & a \end{array}\right]\).
∴ P(n) is true for n = 1.
Let P(n) be true for n = k.
∴ P(k) : \(\left[\begin{array}{ll} a & b \\ 0 & a \end{array}\right]\)k = \(\left[\begin{array}{cc} a^{k} & k a^{k-1} b \\ 0 & a^{k} \end{array}\right]\).
Multiplying both sides by \(\left[\begin{array}{ll} a & b \\ 0 & a \end{array}\right]\), we get :

This shows P(n) is true for n = k + 1 also. Then, by principle of mathematical induction, P(n) is true for all natural numbers n.
![]()
Question 2.
If A = \(\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right]\), prove that An = \(\left[\begin{array}{lll} 3^{n-1} & 3^{n-1} & 3^{n-1} \\ 3^{n-1} & 3^{n-1} & 3^{n-1} \\ 3^{n-1} & 3^{n-1} & 3^{n-1} \end{array}\right]\), n ∈ N.
Solution:

∴ P(n) is true for n = 1.
Let P(n) be true for n = k.
∴ Ak = \(\left[\begin{array}{lll} 3^{k-1} & 3^{k-1} & 3^{k-1} \\ 3^{k-1} & 3^{k-1} & 3^{k-1} \\ 3^{k-1} & 3^{k-1} & 3^{k-1} \end{array}\right]\).
Multiplying both sides by A, we get
L.H.S = AkA = Ak+1

∴ P(n) is true for n = k + 1.
∴ By principle of mathematical inductiqn, P(n) is true for all n, n ∈ N.
Question 3.
If A = \(\left[\begin{array}{ll} 3 & -4 \\ 1 & -1 \end{array}\right]\), then prove that An = \(\left[\begin{array}{cc} 1+2 n & -4 n \\ n & 1-2 n \end{array}\right]\), where n is any positive integer.
Solution:
Let P(n) : An = \(\left[\begin{array}{cc} 1+2 n & -4 n \\ n & 1-2 n \end{array}\right]\), where A = \(\left[\begin{array}{ll} 3 & -4 \\ 1 & -1 \end{array}\right]\).
∴ P(n) is true for n = 1.
Let P(n) be true for n = k.
∴ Ak = \(\left[\begin{array}{cc} 1+2 k & -4 k \\ k & 1-2 k \end{array}\right]\)
Multiplying both sides by A, we get:
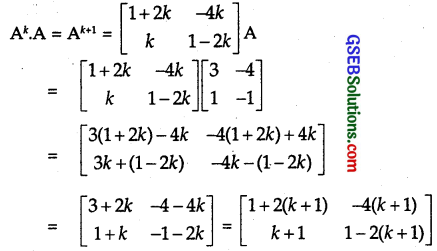
This shows that P(n) is true for n = k + 1 also.
Hence, P(n) is true for all n e N.
![]()
Question 4.
If A and B are symmetric matrices, prove that AB – BA is a skew symmetric matrix.
Solution:
A and B are symmetric matrices. So, A’ = A and B’ = B. Also, (AB)’ = B’A’.
Now, (AB – BA)’ = (AB)’ – (BA)’
= B’A’ – A’B’ = BA – AB .
= – (AB – BA).
Hence, AB – BA is a skew symmetric matrix.
Question 5.
Show that the matrix B’AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.
Solution:
(i) Let A be a symmetric matrix.
⇒ A’ = A
∴ (B’AB)’ = [B'(AB)]’ = (AB) ‘(B)’ = (B’A’)B
= B’AB (∵ A’ = A)
⇒ B’AB is a symmetric matrix.
(ii) Let A be a skew-symmetric matrix.
⇒ A’ = – A.
Now, [B'(AB)]’ = (AB)'(B’)’ = (B’A’)B
= B'(- A)B = – B’AB ( ∵ A’ = A)
⇒ B’AB is a skew symmetric matrix.
Question 6.
Find the values of x, y and z, if the matrix A = \(\left[\begin{array}{ccc} 0 & 2 y & z \\ x & y & -z \\ x & -y & z \end{array}\right]\) satisfies the equation A’A = I3.
Solution:

Question 7.
For what values of x, \(\left[\begin{array}{lll} 1 & 2 & 1 \end{array}\right]\)\(\left[\begin{array}{lll} 1 & 2 & 0 \\ 2 & 0 & 1 \\ 1 & 0 & 2 \end{array}\right]\)\(\left[\begin{array}{l} 0 \\ 2 \\ x \end{array}\right]\)
Solution:

Question 8.
If A = \(\left[\begin{array}{cc} 3 & 1 \\ -1 & 2 \end{array}\right]\), show that A² – 5A + 7I = O. Use this result to find A4.
Solution:

Hence, A² – 5A + 7IA = O.
Multiplying both the sides by A, we get:
A³ – 5A² + 7IA = O … (1)
or A³ – 5A² + 7A = O
∴ A³ = 5A² – 7A

![]()
Question 9.
Find x, if [x – 5 – 1]\(\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right]\)\(\left[\begin{array}{l} x \\ 4 \\ 1 \end{array}\right]\) = O.
Solution:

Question 10.
A manufacturer produces three products x, y and z, which he sells in two markets.
Annual sales are indicated below:

(a) If a unit sale price of x, y and z are ₹ 2.50, ₹ 1.50 and ₹ 1.00 respectively, find the total revenue in each market with the help of matrix algebra.
(b) If the unit cost of the above three commodities are ₹ 2.00, ₹ 1.00 and 50 paise respectively, find the gross profit.
Solution:
(a) Matrix for the products x, y and z is

Matrix corresponding to sale price of each product 
∴ The revenue collected by markets is given by

∴ Revenues in the two markets are ₹ 46000 and ₹ 53000 respectively.
Total revenue = ₹ (46000 + 53000) = ₹ 99000.
(b) The cost price of commodities x, y and z are respectively ₹ 2.00, ₹ 1.00 and ₹ 0.50. Cost price of each market is given below:

Total cost price of the commodities markets I and II are ₹ 31000 and ₹ 36000 respectively.
∴ Total cost price = ₹ (31000 + 36000) = ₹ 67000
∴ Gross profit = Revenue – Cost price
= ₹ (99000 – 67000) = ₹ 32000
![]()
Question 11.
Find the matrix X so that X\(\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right]\) = \(\left[\begin{array}{ccc} -7 & -8 & -9 \\ 2 & 4 & 6 \end{array}\right]\).
Solution:
Let X be of order m x n. Since \(\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right]\) is of the order 2 x 3, so n = 2
Since \(\left[\begin{array}{ccc} -7 & -8 & -9 \\ 2 & 4 & 6 \end{array}\right]\) is of the order 2 x 3. So, m = 2
∴ X is of the order 2 x 2.
Let X = \(\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\)

Equating the corresponding elements,
a + 4b = – 7 … (1)
2a + 5b = – 8 … (2)
3a + 6b = – 9 … (3)
Multiplying (1) by (2), we get
2a + 8b = – 14 … (4)
and 2a + 5b = – 8 … (2)
Subtracting (2) from (4),
3b = -6.
∴ b = – 2
Putting value of b in (1),
a – 8 = – 7 ∴ a = 8 – 7 = 1.
a = 1, b = – 2 satisfies equation (3) also.
Equating the elements of second row,
c + 4d = 2 … (5)
2c + 5d = 4 … (6)
3c + 6d = 6 … (7)
Multiplying equation (5) by 2,
2c + 8d = 4 … (8)
Subtracting (6) from (8),
3d = 4 – 4 = 0. ∴ d = 0
∴ From c + 4d = 2, we get ∴ c = 2
c = 2, d = 0 satisfies equation (7) also.
Thus, a = 1, b = – 2, c = 2, d = 0
Hence, X = \(\left[\begin{array}{ll} 1 & -2 \\ 2 & 0 \end{array}\right]\).
Question 12.
If A and B are square matrices of the same order such that AB = BA, then prove by induction that ABn = BnA. Further, prove that (AB)n = AnBn for all n ∈ N.
Solution:
Let P(n) : ABn = BnA.
But n = 1, AB = BA (Given)
∴ P(n) is true for n = 1.
Let P(n) be true for n = k.
∴ ABk = BkA.
Multiplying both sides by B, we get
L.H.S. = ABk.B = A(BkB) = ABk+1 (Associative property)
and R.H.S. = (BkA)B = Bk(AB)
= Bk(BA) (∵AB = BA)
= (BkB)A
= Bk+1A.
So, P(n) is true for n = k + 1 also.
∴ By principle of mathematical induction.
P(n) is true for all n e N.
(ii) Let P(n) : (AB)n = AnBn
For n = 1, L.H.S. = AB and R.H.S. = AB.
∴ P(n) is true for n = 1.
Let P(n) be true for n = k.
So, (AB)k = AkBk
Multiply both sides by AB. We get
L.H.S. = (AB)k(AB) = (AB)k+1
and R.H.S. = AkBk(AB) = AkBk(BA) (∵ AB = BA)
= Ak(Bk.B)A = Ak(Bk+1A) [∵ ABn = BnA]
= Ak(ABk+1) = Ak+1Bk+1
⇒ P(n) is true for n = k + 1 also.
By principle of mathematical induction,
∴ P(n) is true for all n ∈ N.
![]()
Choose the correct answer in the following questions:
Question 13.
If A = \(\left[\begin{array}{cc} \alpha & \beta \\ \gamma & -\alpha \end{array}\right]\) is such that A² = I, then
(A) 1 + α² + ßγ = 0
(B) 1 – α² + ßγ = 0
(C) 1 – α² – ßγ = 0
(D) 1 + α² – ßγ = 0
Solution:

Question 14.
If a marix is both symmetric and skew symmetric matrix, then
(A) A is a diagonal matrix
(B) A is a zero matrix
(C) A is a square matrix
(D) None of these
Solution:
A is a symmetric matrix, if aij. = aji
A is a skew symmetric matrix, if aij = – aji
If aij = aji = – aji.
⇒ A is a zero matrix.
∴ Part (B) is the correct answer.
![]()
Question 15.
If A is a square matrix such that A² = A, then (1 + A)³ – 7A is equal to
(A) A
(B) 1 – A
(C) 1
(D) 3A
Solution:
A³ = A².A [ ∵ A² = A]
= A.A = A² = A
(1 + A)³ – 7A = (1 + 3A + 3A² + A³) – 7A
= (1 + 3A + 3A + A) – 7A
= (1 + 7A) – 7A .
∴ Hence, Part (C) is the correct answer.