Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.3
![]()
Question 1.
Find the area of the triangle with vertices at the points given in each of the following:
(i) (1, 0), (6, 0), (4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (-2, -3), (3, 2), (-1, -8)
Solution:
(i) Area A of the ∆ whose vertices are (1, 0), (6, 0), (4, 3) is given by
A = \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} 1 & 0 & 1 \\ 6 & 0 & 1 \\ 4 & 3 & 1 \end{array}\right|\)
Expanding with the help of elements of the second column, we get
A = \(\frac { 1 }{ 2 }\)| 3 x (1 – 6) | = \(\frac { 15 }{ 2 }\) = 7 \(\frac { 1 }{ 2 }\) Sq. units.
(ii) The vertices of ∆ ABC are A (2, 7), B (1, 1), C (10, 8).
The area A of ∆ ABC = \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} 2 & 7 & 1 \\ 1 & 1 & 1 \\ 10 & 8 & 1 \end{array}\right|\)
Expanding with the help of elements of I column, we pet
A = \(\frac { 1 }{ 2 }\)[2(1 – 8) – 1(7 – 8) + 10(7 – 1)]
= \(\frac { 1 }{ 2 }\) [- 14 + 1 + 60] = \(\frac { 47 }{ 2 }\) = 23\(\frac { 1 }{ 2 }\) Sq. units.
(iii) The vertices of ∆ ABC are A (-2, -3), B (3, 2), C (-1, -8).
Area of ∆ ABC = – \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\left|\begin{array}{ccc} -2 & -3 & 1 \\ 3 & 2 & 1 \\ -1 & -8 & 1 \end{array}\right|\)
= \(\frac { 1 }{ 2 }\)[-2(2 + 8) + 3(3 + 1) + 1(- 24 + 2)]
= \(\frac { 1 }{ 2 }\)(- 20 + 12 – 22)
= (- 30) = – 15.
∴ Ignoring – ve sign,
Area of ∆ ABC = 15 sq. units.
![]()
Question 2.
Show that the points A (a,b + c), B (b, c + a), C (c, a + b) are collinear.
Solution:
The vertices of ∆ ABC are A (a, b + c), B (b, c + a), C (c, a + b)
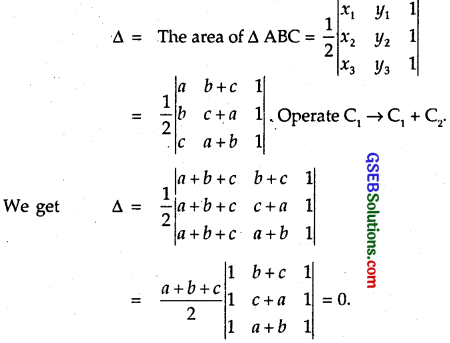
Hence, the points A, B and C are collinear.
Question 3.
Find the value of k, if area of triangle is 4 square units and vertices are:
(i) (k, 0),(4, 0),(0, 2)
(ii) (-2, 0), (1, 4), (0, k)
Solution:
(i) Area A of triangle with vertices (k, 0), (4, 0), (0, 2)
= \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll}
k & 0 & 1 \\
4 & 0 & 1 \\
0 & 2 & 1
\end{array}\right|\)
Expanding with the help of elements of II column, we get
= \(\frac { 1 }{ 2 }\) [- 2(k – 4)] = – (k – 4) = ± 4 (Given)
Taking + ve sign, – (k – 4) = 4 ∴ k = 0.
Taking – ve sign, – (k – 4) = – 4 ∴ k = 8.
(ii) The area A of the triangle whose vertices are (- 2, 0), (0, 4), (0, k)
= \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\left|\begin{array}{ccc} -2 & 0 & 1 \\ 0 & 4 & 1 \\ 0 & k & 1 \end{array}\right|\)
= \(\frac { 1 }{ 2 }\) x (- 2) (4 – k) = k – 4 = ± 4 (Given)
Taking +ve sign, k – 4 = 4 ∴ k = 8.
Taking -ve sign, k – 4 = – 4 ∴ k = 0.
![]()
Question 4.
(i) Find the equation of line joining (1, 2) and (3, 6), using determinants.
(ii) Find the equation of line joining (3,1) and (9, 3), using determinants.
Solution:
(i) Let (x, y) be the third points on the line joining (1, 2) and (3, 6).
The area A of triangle with vertices (x, y), (1, 2) and (3, 6)
= \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\left|\begin{array}{lll} x & y & 1 \\ 1 & 2 & 1 \\ 3 & 6 & 1 \end{array}\right|\)
Since the three points are coliinear,
∴ \(\left|\begin{array}{lll} x & y & 1 \\ 1 & 2 & 1 \\ 3 & 6 & 1 \end{array}\right|\) = 0.
or x(2 – 6) – y(1 – 3) + 1(6 – 6) = 0
or – 4x + 2y = 0
or 2x – y = 0.
It is the required equation of the line.
(ii) Let (x, y) be the third point on the line joining (3, 1) and (9, 3).
The area A of the triangle whose vertices are (x, y), (3, 1) and (9, 3)
= \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\left|\begin{array}{lll} x & y & 1 \\ 3 & 1 & 1 \\ 9 & 3 & 1 \end{array}\right|\)
= \(\frac { 1 }{ 2 }\)[x(1 – 3)-y(3-9)+ 1(9-9)]
= \(\frac { 1 }{ 2 }\)[x(-2)-y(-6)].
As these points are coliinear, the area of the triangle is zero.
∴ x(- 2) – y(- 6) = 0
or 2x – 6y = 0
or x-3y = 0.
It is the required equation of the line.
![]()
Question 5.
If the area of a triangle with vertices (2, – 6), (5, 4) and (k, 4) is 35 sq. units, then k is
(A) 12
(B) – 2
(C) – 12, – 2
(D) 12,- 2
Solution:
The area of the triangle with the given vertices
= \(\frac { 1 }{ 2 }\)\(\left|\begin{array}{lll} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{array}\right|\) = \(\left|\begin{array}{lll} 2 & -6 & 1 \\ 5 & 4 & 1 \\ k & 4 & 1 \end{array}\right|\)
= \(\frac { 1 }{ 2 }\)[2(4 – 4) + 6(5 -k) + 1(20 – 4k) ]
= \(\frac { 1 }{ 2 }\)[(30 – 6k) + 20 – 4k] = \(\frac { 1 }{ 2 }\) [50 – 10k].
The area = 35 sq. units. ∴ \(\frac { 1 }{ 2 }\) [50 – 10k] = ± 35
Taking +ve sign, \(\frac { 1 }{ 2 }\)[50 – 10k] = 35
or 50 – 10k = 70
or 10k = 50 – 70 = – 20
∴ k = -2.
Taking – ve sign, \(\frac { 1 }{ 2 }\)[50 – 10k] = – 35
or 50 – 10k = – 70
or 50 + 70 = 10k
∴ k = 12.
Hence, k = 12, – 2.
Part (D) is the required answer.