Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.6 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.6
![]()
Question 1.
x + 2y = 2
2x + 3y = 3
Solution:
x + 2y = 2
2x + 3y = 3
Let A = \(\left[\begin{array}{ll} 1 & 2 \\ 2 & 3 \end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll} 1 & 2 \\ 2 & 3 \end{array}\right|\) = 3 – 4 = – 1
So, |A| ≠ 0.
∴ System of equations has a unique solution.
Hence, the system of equations is consistent.
Question 2.
2x – y = 5
x + y = 4
Solution:
2x – y = 5
x + y = 4
Let A = \(\left[\begin{array}{ll} 2 & -1 \\ 1 & 1 \end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll} 2 & -1 \\ 1 & 1 \end{array}\right|\) = 2 + 1 = 3 ≠ 0.
∴ System of equations is consistent.
![]()
Question 3.
x + 3y = 5
2x + 6y = 8
Solution:
x + 3y = 5
2x + 6y = 8
Let A = \(\left[\begin{array}{ll} 1 & 3 \\ 2 & 6 \end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll} 1 & 3 \\ 2 & 6 \end{array}\right|\) = 6 – 6 = 0.
Now adj A = \(\left[\begin{array}{ll} 6 & -2 \\ -3 & 1 \end{array}\right]\) = \(\left[\begin{array}{ll} 6 & -3 \\ -2 & 1 \end{array}\right]\) and B = \(\left[\begin{array}{l} 5 \\ 8 \end{array}\right]\)
(adj A).B = \(\left[\begin{array}{ll} 6 & -3 \\ -2 & 1 \end{array}\right]\)\(\left[\begin{array}{l} 5 \\ 8 \end{array}\right]\) = \(\left[\begin{array}{l} 30-24 \\ -10+8 \end{array}\right]\)
= \(\left[\begin{array}{l} 6 \\ -2 \end{array}\right]\) ≠ 0.
∴ Given System of equations is inconsistent.
Question 4.
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
Solution:
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4 or x + y + 2z = \(\frac { 4 }{ a }\)
Let A = \(\left[\begin{array}{lll} 1 & 1 & 1 \\ 2 & 3 & 2 \\ 1 & 1 & 2 \end{array}\right]\), X = \(\left[\begin{array}{l} x \\ y \\ z \end{array}\right]\) and B = \(\left[\begin{array}{c} 1 \\ 2 \\ 4 / a \end{array}\right]\).
Now, |A| = \(\left|\begin{array}{lll} 1 & 1 & 1 \\ 2 & 3 & 3 \\ 1 & 1 & 2 \end{array}\right|\) = 1.(6-2)-1.(4-2)+1.(2-3)
= 4 – 2 – 1 = 1
∴ |A| ≠ 0.
⇒ System of equations is consistent.
Question 5.
3x – y – 2z = 2
2y – z = – 1
3x – 5y = 3
Solution:
The System of equation is
3x – y – 2z = 2
2y – z = – 1
3x – 5y = 3

∴ Given system equation is inconsistent.
![]()
Question 6.
5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = – 1
Solution:
The given System of equation is
5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = – 1

⇒ The given System of equations is consistent.
Question 7.
5x + 2y = 4
7x + 3y = 5
Solution:
The System of equation is
5x + 2y = 4
7x + 3y = 5

Question 8.
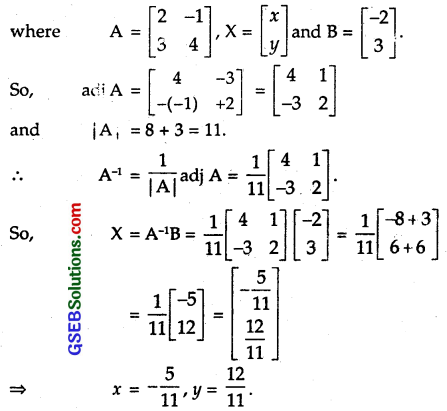
2x – y = – 2
3x + 4y = 3
Solution:
The system of equations is
2x – y = – 2
3x + 4y = 3
This may be wirtten as AX = B.
or X = A-1B,
Question 9.
4x – 3y = 3
3x – 5y = 7
Solution:
The system of equations is
4x – 3y = 3
3x – 5y = 7
This system of equations may be put as AX = B or X = A-1B,

Question 10.
5x + 2y = 3
3x + 2y = 5
Solution:
The system of equations is
5x + 2y = 3
3x + 2y = 5
This system of equations may be written as AX = B or X = A-1B,

Question 11.
2x + y + z = 1
x – 2y – z = \(\frac { 3 }{ 2 }\)
3y – 5z = 9
Solution:
The given system of equations is
2x + y + z = 1
x – 2y – z = \(\frac { 3 }{ 2 }\)
3y – 5z = 9
This system of equations may be written as AX = B or X = A-1B,

[+ or – signs are put according as ,(-i)i+i is +ve or -ve respectively. Minors of corresponding elements are written in brackets ()].

![]()
Question 12.
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
Solution:
The given system of equations is
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
which may be written as AX = B or X = A-1B,
where A = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
2 & 1 & -3 \\
1 & 1 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
4 \\
0 \\
2
\end{array}\right]\)
To find adj A, we calculate the cofactors of the elements of A.

Question 13.
2x + + 3z = 5
x – 2y + z = – 4
3x – y – 2z = 3
Solution:
The given system of equations can be written as
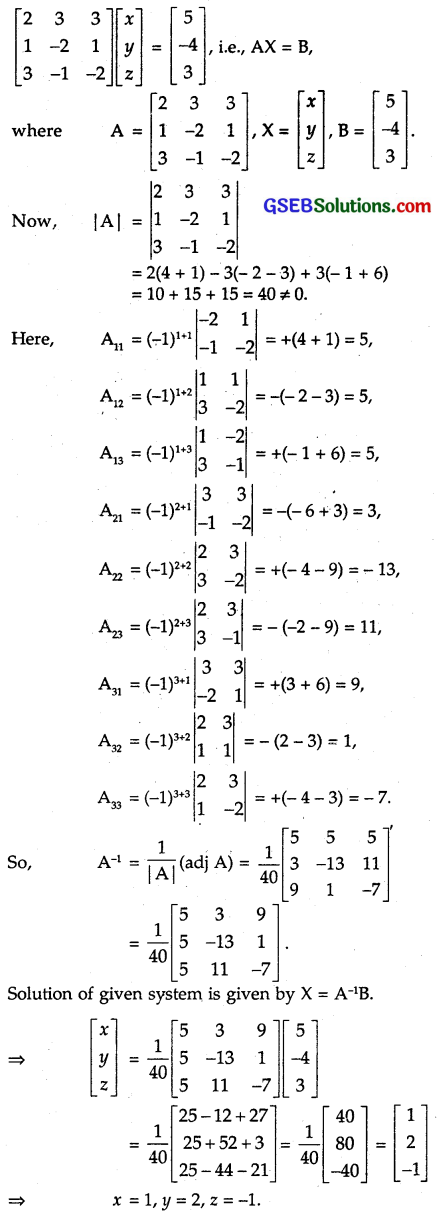
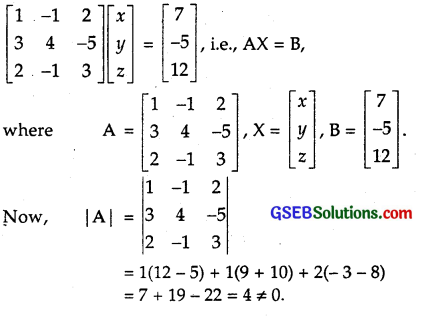
Question 14.
x – y + 2z = 7
3x + 4y – 5z = – 5
2x – y + 3z = 12
Solution:
The given system of equation can be written as
∴ A-1 exists and hence the given equations have a unique solution.
Here,

![]()
Question 15.
If A = \(\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), find A-1. Using A-1, solve the following system of linear equations:
2x – 3y + 5z = 11, 3x + 2y – 4z = – 5, x + y – 2z = – 3.
Solution:
The given system of equations can be written as
\(\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\)\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
11 \\
-5 \\
-3
\end{array}\right]\), i.e., AX = B,
Now, |A| = \(\left|\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right|\)
= 2(- 4 + 4) + 3(- 6 + 6) + 5(3 – 2)
= 0 – 6 + 5 = – 1 ≠ 0.
∴ A-1 exists and hence the given equations have a unique solution.

Question 16.
The cost of 4 kg onions, 3 kg wheat and 2kg rice is ₹ 60. The cost of 2 kg onions, 4 kg wheat and 6 kg rice ₹ 90. The cost of 6 kg onions, 2 kg wheat and 3 kg rice is 70. Find the cost of each item per kg by matrix method.
Solution:
Let the cost of ornons, wheat and rice per kg be ₹ x, ₹ y and ₹ z respectively.
The cost of 4 kg onions, 3 kg wheat and 2 kg rice = ₹ 60.
∴ 4x + 3y + 2z = 60. … (1)
The cost of 2 kg onions, 4 kg wheat and 6 kg rice = ₹ 90
∴ 2x + 4y + 6z = 90 … (2)
The cost of 6 kg onions, 2 kg wheat and 3 kg rice = ₹ 70
∴ 6x + 2y + 3z = 70 … (3)
The system of equations is
4x + 3y + 2z = 60
x + 2y + 3z = 45 [Dividing equation (2) by 2]
6x + 2y + 3z = 70,
which may be written as
AX = B or X = A-1B,

⇒ The cost of onions, wheat and rice per kg are ₹ 5, ₹ 8, ₹ 8 respectively.

Also, we have given equations as
x – 2y = 10
2x – y – z = 8
and – 2y + z = 7
or \(\left[\begin{array}{ccc}
1 & -2 & 0 \\
2 & -1 & -1 \\
0 & -2 & 1
\end{array}\right]\)\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
10 \\
8 \\
7
\end{array}\right]\)
or CX = D,
where C = \(\left[\begin{array}{ccc}
1 & -2 & 0 \\
2 & -1 & -1 \\
0 & -2 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\)
and D = \(\left[\begin{array}{l}
10 \\
8 \\
7
\end{array}\right]\).
We know that (A’)-1 = (A-1)’.
∴ C’ = \(\left[\begin{array}{ccc}
1 & -2 & 0 \\
– 2 & -1 & -2 \\
0 & – 1 & 1
\end{array}\right]\)
![]()