GSEB Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.2

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.2

Question 1.
sin(x² + 5)
Solution:
Let y = sin(x² + 5)
Put x² + 5 = t
∴ y = sin t and t = x² + 5.
So, \(\frac { dy }{ dx }\) = \(\frac { dy }{ dt }\). \(\frac { dt }{ dx }\) = cos t. \(\frac { dt }{ dx }\)
= cos(x² + 5)\(\frac { d }{ dx }\)(x² + 5)
= cos(x² + 5) x 2x = 2x cos((x² + 5).

Question 2.
cos (sin x)
Solution:
Let y = cos (sin x)
Put sin x = t
∴ y = sin t and t = sin x.
∴ \(\frac { dy }{ dx }\) = – sin t, \(\frac { dt }{ dx }\) = cos x.
∴ \(\frac { dy }{ dx }\) = \(\frac { dy }{ dt }\) . \(\frac { dt }{ dx }\) = ( – sin t) x (cos x)
Putting value of t, we get
\(\frac { dy }{ dx }\) = – sin (sin x) × cos x
= – [sin(sin x)] cos x.

Question 3.
sin (ax + b)
Solution:
Let y = sin (ax + b).
Put ax + b = t.
∴ y = sin t and t = ax + b.
∴ \(\frac { dy }{ dx }\) = cos t, \(\frac { dt }{ dx }\) = \(\frac { d }{ dx }\) (ax + b) = a.
Now, \(\frac { dy }{ dx }\) = \(\frac { dy }{ dt }\) . \(\frac { dt }{ dx }\) = ( cos t) x a
= a cos (ax +b)

Question 4.
sec(tan(\(\sqrt{x}\))
Solution:
Let y = sec(tan(\(\sqrt{x}\))
put \(\sqrt{x}\) = t and s = tan t.
⇒ y = sec s, s = tan t and t = \(\sqrt{x}\).
Now, \(\frac { dy }{ dx }\) = \(\frac { dy }{ ds }\) x \(\frac { ds }{ dt }\) x \(\frac { dt }{ dx }\) … (1)
So, y = sec s. ∴ \(\frac { dy }{ ds }\) = sec s tan s
Also, s = tan t. ∴ \(\frac { ds }{ dt }\) = sec² t.
Further, t = \(\sqrt{x}\) ∴ \(\frac { dt }{ dx }\) = \(\frac{1}{2 \sqrt{x}}\)
Putting these values in (1), we get
\(\frac { dy }{ dx }\) = (sec (tan s) (sec² t)\(\left(\frac{1}{2 \sqrt{x}}\right)\)
= sec (tan t) tan (tan (t). sec²\(\sqrt{x}\) . \(\frac{1}{2 \sqrt{x}}\)
= \(\frac{1}{2 \sqrt{x}}\)sec tan\(\sqrt{x}\) tan (tan (\(\sqrt{x}\))).sec²\(\sqrt{x}\).

Question 5.
\(\frac{\sin (a x+b)}{\cos (c x+d)}\)
Solution:

Question 6.
cos x³. sin² (x⁵)
Solution:
Let y = cos x³ sin²(x⁵) = uv,
where u = cosx³ and v = sin2(x⁵).
To find \(\frac { du }{ dx }\), put x³ = t.
∴ u = cos t, t = x³.
∴ \(\frac { du }{ dx }\) = – sin t and \(\frac { dt }{ dx }\) = 3x².
∴ \(\frac { du }{ dx }\) = \(\frac { du }{ dt }\) x \(\frac { dt }{ dx }\) = (- sin t) (3x²)
= – sin x³ (3x²) = – 3x² sin x³.
To find \(\frac { du }{ dx }\), put t = x⁵ and sin t = s.
∴ v = s², s = sin t and t = x⁵.
∴ \(\frac { dv }{ ds }\) = 2s, \(\frac { ds }{ dt }\) = cos t and \(\frac { dt }{ dx }\) = 5x⁴
= 2s x cos t x 5a⁴ = 2 sin t cos t x 5x⁴
= 10x⁴ sin x⁵ cos x⁵
Now, y = uv = (cos x³) (sin2 x³)
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) x v + u x \(\frac { dv }{ dx }\)
∴ \(\frac { dy }{ dx }\) = (- 3x² sin x³) × sin²x⁵ + cos x³ x 10x⁴ sinx⁵ cos x⁵
= – 3x² sin x³ sin²x⁵ + 10x⁴ cos x³ sin x⁵ cos x⁵
= x² sin x⁵ (- 3 sin x³ sin x⁵ + 10x² cos x³ cos x³).

Question 7.
\(\sqrt{\cot \left(x^{2}\right)}\)
Solution:

Question 8.
cos\(\sqrt{x}\)
Solution:

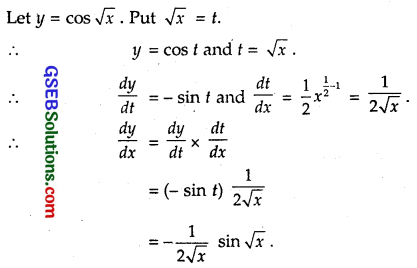
Question 9.
Prove that the function f is given by f(x) = |x-1|, x ∈ R is not differentiable at x = 1.
Solution:
The given function may be written as

So, R.H.D ≠ L.H.D
⇒ f is not differentiable at x = 1.

Question 10.
Prove that the greatest integer function defined by f(x) = [x], 0 < x < 3 is not differentiable at x = 1 and x = 3.
Solution:
(i) At x = 1,

∴ f is not differentiable at x = 1.

(ii) At x = 3,

⇒ f is not differentiable at x = 3.