Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.1
![]()
Question 1.
Prove that the function f(x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
Solution:
(i) At x = 0, \(\lim _{x \rightarrow 0}\)f(x) = \(\lim _{x \rightarrow 0}\) (5x – 3) = – 3
and f(0) = -3.
∴ f is continuous at x = 0.
(ii) At x = – 3, \(\lim _{x \rightarrow -3}\)f(x) = \(\lim _{x \rightarrow -3}\) (5x – 3) = -18
and f(- 3) = – 18.
∴ f is continuous at x = – 3.
(iii) At x = 5, \(\lim _{x \rightarrow 5}\) f(x) = \(\lim _{x \rightarrow 5}\) (5x – 3) = 22
and f(5) = 22
∴ f is continuous at x = 5.
Use this handy free online Implicit Differentiation Calculator tool to get the accurate output of an equation in a fraction of seconds.
![]()
Question 2.
Examine the continuity of the function f(x) = 2x² – 1 at x = 3.
Solution:
\(\lim _{x \rightarrow 3}\) f(x) = \(\lim _{x \rightarrow 3}\) (2x² – 1) = 17
and f(3) = 17.
∴ f is continuous at x = 3.
Question 3.
Examine the following functions for continuity:
(a) f(x) = x – 5
(b) f(x) = \(\frac { 1 }{ x-5 }\)
(c) f(x) = \(\frac{x^{2}-25}{x+5}\)
(d) f(x) = |x-5|
Solution:
(a) f(x) = x – 5
x – 5 is a polynomial.
Therefore, it is continuous at each x ∈ R.
(b) f(x) = \(\frac { 1 }{ x-5 }\)
At x = 5, f(x) is not defined.
∴ f is not continuous at x = 5.
When x ≠ 5, \(\lim _{x \rightarrow c}\) = \(\frac { 1 }{ c-5 }\)
Also, f(c) = \(\frac { 1 }{ c-5 }\)
∴ f is continuous at x ∈ R – {5}.
(c) f(x) = \(\frac{x^{2}-25}{x+5}\)
At x = – 5, function/is not defined.
∴ f is discontinuous at x = – 5.
At x = c ≠ – 5,
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) \(\frac{x^{2}-25}{x+5}\) = c – 5
and f(c) = c – 5.
∴ f is continuous for all x ∈ R – {- 5).
(d) f(x) = |x – 5|
At x = 5, f(5) = |5 – 5| = 0
\(\lim _{x \rightarrow c}\) |x – 5| = 0
∴ f is continuous at x = 5.
At x = c > 5,
\(\lim _{x \rightarrow c}\) |x – 5| = c – 5 [c > 5]
Also, f(c) = c – 5.
∴ f is continuous at x = c > 5.
Similarly, at x = c < 5,
\(\lim _{x \rightarrow c}\) |x – 5| = 5 – c and f(c) = 5 – c.
∴ f is continuous at x = c < 5.
Thus, f is continuous for all x ∈ R.
![]()
Question 4.
Prove that the function f(x) = xn is continuous at x = n, when n is a positive integer.
Solution:
f(x) = xn is a polynomial which is continuous for all x ∈ R.
Hence, f is continuous at x = n, n ∈ N.
Question 5.
Is the function f defined by
f(x) = \(\left\{\begin{array}{l}
x, \text { if } x \leq 1 \\
5, \text { if } x>1
\end{array}\right.\)
continuous at x = 0?, At x = 1?, At x = 2?
Solution:
(i) At x = 0,
\(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0^{-}}\) x = 0.
\(\lim _{x \rightarrow 0^{+}}\) f(x) = \(\lim _{x \rightarrow 0^{+}}\) x = 0.
Also, f(0) = 0.
∴ f is continuous at x = 0.
(ii) At x =1,
\(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (x) = 1.
\(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) (x) = 5.
\(\lim _{x \rightarrow 1^{-}}\) f(x) ≠ \(\lim _{x \rightarrow 1^{+}}\) (x)
∴ f is discontinuous at x = 1.
(iii) At x = 2,
\(\lim _{x \rightarrow 2}\) f(x) = 5 and f(2) = 5.
∴ f is continuous at x = 2.
![]()
Question 6.
f(x) = \(\left\{\begin{array}{l}
2 x+3, x \leq 2 \\
2 x-3, x>2
\end{array}\right.\)
Solution:
f(x) = \(\left\{\begin{array}{l}
2 x+3, x \leq 2 \\
2 x-3, x>2
\end{array}\right.\)
At x – 2, L.H.L. = \(\lim _{x \rightarrow 2^{-}}\) (2x + 3) = 7
f(2) = 2 x 2 + 3 = 7
R.H.L. = \(\lim _{x \rightarrow 2^{+}}\) (2x – 3) = 2 x 2 – 3 = 1
⇒ L.H.L. ≠ R.H.L.
∴ f is discontinuous at x = 2.
At x = c < 2, \(\lim _{x \rightarrow c}\) (2x + 3) = 2c + 3 = f(c).
f is continuous at x = c < 2. At x = c > 2, \(\lim _{x \rightarrow c}\) (2x – 3) = 2c – 3 = f(c).
∴ f is continuous at x = c > 2.
⇒ Point of discontinuity is x = 2.
Question 7.
f(x) = \(\left\{\begin{array}{l}
|x|+3, \text { if } x \leq-3 \\
-2 x, \quad \text { if }-3<x<3 \\ 6 x+2, \text { if } x>3
\end{array}\right.\)
Solution:
f(x) = \(\left\{\begin{array}{l}
|x|+3, \text { if } x \leq-3 \\
-2 x, \quad \text { if }-3<x<3 \\ 6 x+2, \text { if } x>3
\end{array}\right.\)
At x = – 3, L.H.L. = \(\lim _{x \rightarrow 3^{-}}\) (|x|+3)
= \(\lim _{x \rightarrow -3^{-}}\) (-x + 3) = 3 + 3 = 6.
f(- 3) = |- 3| + 3 = 6.
R.H.L. = \(\lim _{x \rightarrow -3^{+}}\) f(x) = \(\lim _{x \rightarrow -3^{+}}\) (- 2x) = 6.
L.H.L. = R.H.L. = f(- 3).
⇒ f is continuous at x = – 3.
At x = 3, L.H.L. = \(\lim _{x \rightarrow 3^{-}}\) f(x) = \(\lim _{x \rightarrow 3^{-}}\) (- 2x) = – 6
R.H.L. = \(\lim _{x \rightarrow 3^{+}}\) f(x) = \(\lim _{x \rightarrow 3^{+}}\) (6x + 2) = 20
f(3) is not defined.
∴ L.H.L. ≠ R.H.L. ≠ f(3)
∴ f is discontinuous at x = 3.
At x = c < – 3,
\(\lim _{x \rightarrow -c}\) (|x| + 3) = – c + 3 = f(c)
⇒ \(\lim _{x \rightarrow -c}\) f(x) = f(c)
⇒ f is continuous at x = c < – 3.
At x = c, when – 3 < x < 3,
\(\lim _{x \rightarrow 1^{-}}\) (- 2x) =-2c =f(c) ⇒ \(\lim _{x \rightarrow 1^{-}}\) f(x) = f(c).
∴ f is continuous at x = c, where -3 < c < 3.
At x = c, \(\lim _{x \rightarrow c}\)(6x + 2) = 6c + 2 = f(c).
⇒ \(\lim _{x \rightarrow c}\)f(x) = f(c)
⇒ f is continuous at x = c > 3.
![]()
Question 8.
f(x) = \(\left\{\begin{array}{ll}
\frac{|x|}{x}, & \text { if } x \neq 0 \\
0, & \text { if } x=0
\end{array}\right.\)
Solution:

Question 9.
f(x) = \(\left\{\begin{array}{ll}
\frac{x}{|x|}, & \text { if } x<0 \\
-1, & \text { if } x \geq 0
\end{array}\right.\)
Solution:

∴ \(\lim _{x \rightarrow c}\)f(x) = f(c) ⇒ f is continuous at x = c < 0. At x = c > 0, \(\lim _{x \rightarrow c}\) f(x) = – 1
Also, f(c) = – 1.
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c) ⇒ f is continuous at x = c > 0.
There is no point of discontinuity for this function in its domain.
![]()
Question 10.
f(x) = \(\left\{\begin{array}{ll}
x+1, & \text { if } x \geq 1 \\
x^{2}+1, & \text { if } x<1 \end{array}\right.\)
Solution:
f(x) = \(\left\{\begin{array}{ll}
x+1, & \text { if } x \geq 1 \\
x^{2}+1, & \text { if } x<1 \end{array}\right.\)
At x = 1, L.H.L. = \(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (x² + 1) = 2,
R.H.L. = \(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) (x + 1) = 2
and f(1) = 1 + 1 = 2.
⇒ f is continuous at x = 1.
At x = c > 1, \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x + 1) = c + 1 = f(c).
⇒ f is continuous at x = c > 1.
At x = c < 1, \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x² + 1) = c² + 1 = f(c).
⇒ f is continuous at x = c < 1.
There is no point of discontinuity at any noint x ∈R.
Question 11.
f(x) = \(\left\{\begin{array}{l} x^{3}-3, \text { if } x \leq 2 \\ x^{2}+1, \text { if } x>2 \end{array}\right.\)
Solution:
\(\left\{\begin{array}{l} x^{3}-3, \text { if } x \leq 2 \\ x^{2}+1, \text { if } x>2 \end{array}\right.\)
At x = 2,
L.H.L. = \(\lim _{x \rightarrow 2^{-}}\) (x³ – 3) = 8 – 3 = 5,
R.H.L. = \(\lim _{x \rightarrow 2^{+}}\) (x² + 1) = 4 + 1 = 5
and f(2) = 2³ – 3 = 8 – 3 = 5.
⇒ f is continuous at x = 2.
At x = c < 2, \(\lim _{x \rightarrow c}\) (x³ – 3) = c³ – 3 = f(c).
⇒ f is continuous at x < 2.
At x = c > 2, \(\lim _{x \rightarrow c}\) (x² + 1) = c² + 1 = f(c).
⇒ f is continuous at x > 2.
Hence, f is continuous for all x ∈ R.
∴ There is no point of discontinuity.
Question 12.
f(x) = \(\left\{\begin{array}{l}
x^{10}-1, \text { if } x \leq 1 \\
x^{2}, \quad \text { if } x>1
\end{array}\right.\)
Solution:

⇒ f is continuous at x = 1.
At x = c < 1, \(\lim _{x \rightarrow c}\) (x<sup>10</sup> – 1) = c<sup>10</sup> – 1 = f(c).
⇒ f is continuous at x < 1.
At x = c > 1, \(\lim _{x \rightarrow c}\) (x²) = c² = f(c).
⇒ f is continuous at x > 1.
Hence, f is continuous at all points x ∈ R – [1]
∴ Point of discontinuity is x = 1.
![]()
Question 13.
Is the function defined by
f(x) = \(\left\{\begin{array}{l}
x+5, \text { if } x \leq 1 \\
x-5, \text { if } x>1
\end{array}\right.\)
a continuous function?
Solution:
At x = 1,
L.H.L. = \(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (x + 5) = 6,
R.H.L. = \(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) (x – 5) = – 4,
and
f(1) = 1 + 5 = 6
f(1) = L.H.L ≠ R.H.L
⇒ f is continuous at x = 1.
At x = c < 1, \(\lim _{x \rightarrow c}\) (x + 5) = c + 5 = f(c).
⇒ f is continuous at x < 1.
At x = c > 1, \(\lim _{x \rightarrow c}\) (x – 5) = c – 5 = f(c).
⇒ f is continuous at x > 1.
⇒ f is continuous at all points x ∈ R, except x = 1.
Question 14.
f(x) = \(\left\{\begin{array}{l}
3, \text { if } 0 \leq x \leq 1 \\
4, \text { if } 1<x<3 \\
5, \text { if } 3 \leq x \leq 10
\end{array}\right.\)
Solution:
f(x) = \(\left\{\begin{array}{l}
3, \text { if } 0 \leq x \leq 1 \\
4, \text { if } 1<x<3 \\
5, \text { if } 3 \leq x \leq 10
\end{array}\right.\)
In the interval 0 ≤ x < 1, f(x) = 3.
f is continuous in this interval.
At x = 1,
L.H.L. = \(\lim _{x \rightarrow 1^{-}}\) f(x) = 3
R.H.L. = \(\lim _{x \rightarrow 1^{+}}\) f(x) = 4
⇒ f is discontinous at x = 1 because L.H.L. ≠ RH.L
In the interval 1 < x < 3, f(x) = 4.
∴ f is continuous in this interval.
At x = 3,
L.H.L. = \(\lim _{x \rightarrow 3^{-}}\) f(x) = 4
R.H.L. = \(\lim _{x \rightarrow 3^{+}}\) f(x) = 5
⇒ f is discontinous at x = 1 because L.H.L. ≠ RH.L
In the interval 3 ≤ x ≤ 10, f(x) = 5.
∴ f is continuous in this interval except for x = 3
⇒ f is not continous at x = 1 and x = 3.
![]()
Question 15.
f(x) = \(\left\{\begin{array}{l}
2 x, \text { if } x<0 \\ 0, \text { if } 0 \leq x \leq 1 \\ 4 x, \text { if } x>1
\end{array}\right.\)
Solution:
At x = 0,
L.H.L. = \(\lim _{x \rightarrow 0^{-}}\) (2x) = 0
R.H.L. = \(\lim _{x \rightarrow 0^{+}}\) (0) = 0
and f(0) = 0.
⇒ f is continous at x = 0.
At x = 1,
L.H.L. = \(\lim _{x \rightarrow 1^{+}}\) (0) = 0
R.H.L. = \(\lim _{x \rightarrow 1^{+}}\) (4x) = 4
and f(1) = 0.
∴ f(1) = L.H.L. ≠ R.H.L.
∴ f is continuous at x = 1.
When x < 0, f(x) = 2x, being a polynomial, is continuous at all points x < 0. When x > 1, f(x) = 4x, being a polynomial, is continuous at all points x > 1.
When 0 ≤ x ≤ 1, f(x) = 0 is a continuous function, except for the point x = 1.
∴ The point of discontinuity is x =1.
Question 16.
f(x) = \(\left\{\begin{array}{ll}
-2, & \text { if } x<-1 \\
2 x, & \text { if }-1<x<1 \\ 2, & \text { if } x>1
\end{array}\right.\)
Solution:
At x = – 1,
L.H.L. = \(\lim _{x \rightarrow 1^{-}}\) f(x) = -2,
f(-1) = – 2
and R.H.L. = \(\lim _{x \rightarrow 1^{+}}\) f(x) = – 2.
⇒ f is continous at x = – 1.
At x = 1,
L.H.L. = \(\lim _{x \rightarrow 1^{-}}\) f(x) = 2
f(1) = 2
R.H.L. = \(\lim _{x \rightarrow 1^{+}}\) f(x) = 2
∴ f is continuous at x = 1.
Hence, f is continuous function.
![]()
Question 17.
Find the values of a and b so that the function defined by
f(x) = \(\left\{\begin{array}{ll}
a x+1, & \text { if } x \leq 3 \\
b x+3, & \text { if } x>3
\end{array}\right.\)
is continuous at x = 3.
Solution:
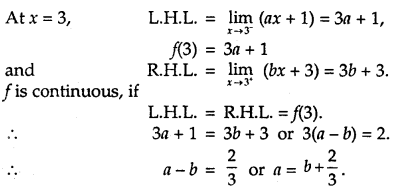
For any arbitary value of b, we can find the value of a corresponding to the value of b. Thus, there are infinitely many values of a and b.
Question 18.
For what value of λ, is the function
f(x) = \(\left\{\begin{array}{l}
\lambda\left(x^{2}-2 x\right), \text { if } x \leq 0 \\
4 x+1, \quad \text { if } x>0
\end{array}\right.\)
continuous at x = 0? What about continuity at x = 1?
Solution:
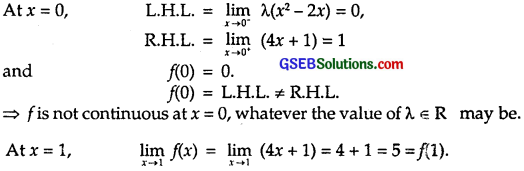
So, f is continuous at x = 1.
⇒ f is not continuous at x = 0 for any value of λ, but f is continuous at x = 1 for all values of λ.
![]()
Question 19.
Show that function defined by g(x) = x – [x] is discontinuous at all integral points. Here, [x] denotes the greatest integer less than or equal to x.
Solution:
Let c be an integer.

⇒ f is not continuous at all integral points.
Note:
To find :
Question 20.
Is the function defined by x² – sin x + 5 continuous at x = π?
Solution:
Let f(x) = x² – sin x + 5.

Hence, f is continuous at x = π.
Alternatively:
g(x) = x² + 5 is a polynomial and h(x) = sin x
∴ g is continuous for all x ∈ R.
h(x) = sin x, which is continuous for all x ∈ R
∴ f = g – h is also continuous for x ∈ R.
Question 21.
Discuss the continuity of the following functions:
(a) f(x) = sin x + cos x
(b) f(x) = sin x – cos x
(c) f(x) = sin x.cos x
Solution:

As above, f is continuous for all x ∈ R.
(c)
f(x) = sin x cos x = \(\frac { 1 }{ 2 }\)(2 sin x cos x)
= \(\frac { 1 }{ 2 }\) sin 2x.
Again, f is continuous for all x ∈ R.
![]()
Question 22.
Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
Solution:
Let f(x) = cos x.
At x = c, c ∈ R,
\(\lim _{x \rightarrow c}\) cos x = cos c = f(c).
∴ f is continuous for all values of x ∈ R.
(b) Let f(x) = sec x.
sec x is not defined at x = (2n + 1) \(\frac { π }{ 2 }\), n ∈Z.
Also, at x = \(\frac { π }{ 2 }\),

∴ f is not continuous at x = \(\frac { π }{ 2 }\) or at x = (2n + 1) \(\frac { π }{ 2 }\).
At x = c ≠ (2n + 1)\(\frac { π }{ 2 }\),
\(\lim _{x \rightarrow c}\) sec x = sec c = f(c).
Hence, f is continuous at x ∈ R except at x = (2n + 1) \(\frac { π }{ 2 }\), where n ∈ Z.
(c) f(x) = cosec x
f is not defined at x = nπ.
⇒ f is not continuous at x = nπ.
(d) f(x) = cot x
f is not defined at x = nπ.

Thus, f is not continuous at x = π or at x = nπ.
At x = c ≠ nπ,
\(\lim _{x \rightarrow c}\) cot x = cot c = f(c).
f is continuous at all points x ∈ R except x = nπ, where n ∈ Z.
Question 23.
Find all the points of discontinuity of f, where
f(x) = \(\left\{\begin{array}{l}
\frac{\sin x}{x}, \text { if } x<0 \\
x+1, \text { if } x \geq 0
\end{array}\right.\)
Solution:
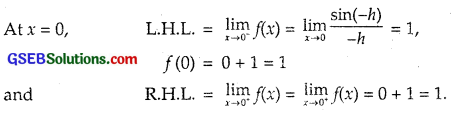
∴ f is continuous at x = 0.
When x < 0, sin x and x both are continuous.
∴ \(\frac { sin x }{ x }\) is also continuous.
When x > 0, f(x) = x + 1 is a polynomial.
∴ f is continuous.
⇒ f is not discontinuous at any point.
Question 24.
Determine if f defined by f(x) = \(\left\{\begin{array}{l}
x^{2} \sin \frac{1}{x}, \text { if } x \neq 0 \\
0, \quad \text { if } x=0
\end{array}\right.\) is a continuous function?
Solution:

sin \(\frac { 1}{ h }\) lies between -1 and 1, a finite quantity.
∴ h² sin \(\frac { 1}{ h }\) → 0 as h → 0.
∴ L.H.L. = 0
Similarly, \(\lim _{x \rightarrow 0^{+}}\)(x² sin \(\frac { 1}{ h }\)) = 0
Also, f(0) = 0 [Gievn]
∴ L.H.L = R.H.L = f(c)
∴ f is continuous for all x ∈ R.
![]()
Question 25.
Examine the continuity of f, where f is defined by f(x) = \(\left\{\begin{array}{r}
\sin x-\cos x, \text { if } x \neq 0 \\
-1, \quad \text { if } x=0
\end{array}\right.\)
Solution:

∴ f is continuous at x = 0.
Alternatively :
sin x and cos x both are continuous for all x ∈ R.
∴ sin x – cos x is continuous for all x ∈ R.
⇒ f is continuous for all x ∈ R for all x ∈ R.
Question 26.
f(x) = \(\left\{\begin{array}{r}
\frac{k \cos x}{\pi-2 x}, \text { if } x \neq \frac{\pi}{2} \\
3, \text { if } x=\frac{\pi}{2}
\end{array}\right. \text { at } x=\frac{\pi}{2}\)
Solution:
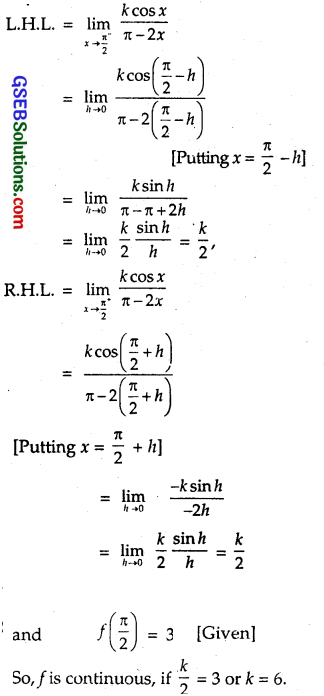
Question 27.
The function is defined by
f(x) = \(\left\{\begin{array}{l}
k x^{2}, \text { if } x \leq 2 \\
3, \text { if } x>2
\end{array}\right. \text { at } x=2\)
Solution:

Question 28.
The function is defined by
f(x) = \(\left\{\begin{array}{ll}
k x+1, & \text { if } x \leq \pi \\
\cos x, & \text { if } x>\pi
\end{array}\right. \text { at } x=\pi\)
Solution:

Question 29.
The function is defined by
f(x) = \(\left\{\begin{array}{l}
k x+1, \text { if } x \leq 5 \\
3 x-5, \text { if } x>5
\end{array}\right. \text { at } x=5\)
Solution:
L.H.L. = \(\lim _{x \rightarrow 5^{-}}\) (kx + 1) = 5k +1,
f(5) = k . 5 + 1 – 5k + 1
and
R.H.L. = \(\lim _{x \rightarrow 5^{+}}\) (3x – 5) = 10.
f is continuous, if L.H.L. = R.H.L. = f(5).
∴ 5k + 1 = 10
∴ k = \(\frac { 9 }{ 5 }\).
![]()
Question 30.
Find the values of a and b such that the function defined by
f(x) = \(\left\{\begin{array}{cl}
5, & \text { if } x \leq 2 \\
a x+b, & \text { if } 2<x<10 \\
21, & \text { if } x \geq 10
\end{array}\right.\)
is a continous function.
Solution:
At x = 2, L.H.L. = \(\lim _{x \rightarrow 2^{-}}\) (5) = 5,
f(2) = 5
and R.H.L. = \(\lim _{x \rightarrow 2^{+}}\) (ax + b) = 2a + b.
f is continuous at x = 2, if 2a + b = 5 … (1)
At x = 10, L.H.L. = \(\lim _{x \rightarrow 10^{-}}\) f(x) = \(\lim _{x \rightarrow 10^{-}}\) (ax + b)
= 10a + b
and R.H.L. = \(\lim _{x \rightarrow 10^{+}}\) f(x) = \(\lim _{x \rightarrow 10^{+}}\) (21) = 21.
Also, f(10) = 21.
∴ f is continuous at x = 10, if 10a + b = 21. … (2)
Subtracting (1) from (2),
8a = 21 – 5 = 16. ∴ a = 2.
From (1), 2 x 2 + b – 5. ∴ b = 1.
Hence, a = 2 and b = 1.
Question 31.
Show that the function defined by f(x) = cos x² is a continuous function.
Solution:
Now, f(x) = cos x².
Let g(x) = cos x and h(x) = x².
∴ (goh) (x) = g(h(x)) = cos x².
Now, g and h both are continuous for all x ∈ R.
∴ f(x) = (goh)(x) = cos x² is also continuous at all x ∈ R.
![]()
Question 32.
Show that the function defined by f(x) = | cos x | is a continuous function.
Solution:
Let g(x) = | x | and f(x) – cos x.
∴ f(x) = (goh)(x) = g(h(x))
= g(cos x) = | cos x|.
Now, g{x) = | x | and h(x) = cos x
both are continuous for all values of x ∈ R.
∴ (goh)(x) is also continuous.
Hence, f(x) = (goh)(x)
= | cos x | is continuous for all values of x ∈ R.
Question 33.
Examine if sin | x | is a continuous function.
Solution:
Let g(x) = sin x and h(x) = | x |.
∴ (goh)(x) = g(h(x)) = g(| X |) = sin | x | = f(x).
Now, g(x) = sin x and h(x) = | x |
both are continuous for all x ∈ R.
∴ f(x) = (goh)(x)
= sin | x | is continuous at all x ∈ R.
![]()
Question 34.
Find all the points of discontinuity of f defined by f(x) = |x| – |x+1|.
Solution:

∴ f is continous at x = 0
⇒ There is no point of discontinuity.
Hence, f is continuous for all x ∈ R.