Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.3
![]()
Question 1.
2x + 3y = sin x
Solution:
2x + 3y = sin x.
Differentiating w.r.t. x,
2x + 3\(\frac { dy }{ dx }\) = cos x. ∴ \(\frac { dy }{ dx }\) = \(\frac { 1 }{ 3 }\)(cosx-2)
2x + 3y = sin y.
Question 2.
2x + 3 y = sin y
Solution:
Differentiating w.r.t. x,
2 + 3\(\frac { dy }{ dx }\) = cos y \(\frac { dy }{ dx }\) or (cos y – 3) \(\frac { dy }{ dx }\) = 2
∴ \(\frac { dy }{ dx }\) = \(\frac { 2 }{ cos y – 3 }\).
ax + by² = cos y.
Question 3.
ax + by² = cos y
Solution:
Differentiating w.r.t. x,
a + 2by\(\frac { dy }{ dx }\) = – sin y \(\frac { dy }{ dx }\)
or (2b + sin y) \(\frac { dy }{ dx }\) = – a
∴ \(\frac { dy }{ dx }\) = – \(\frac { a }{ 2b + sin y }\).
xy + y² = tan x + y.
Question 4.
xy + y² = tan x + y
Solution:
Differentiating w.r.t. x,
(1.y + x \(\frac { dy }{ dx }\)) = sec² x + \(\frac { dy }{ dx }\)
or (x + 2y – 1) \(\frac { dy }{ dx }\) = sec² x – y
∴ \(\frac { dy }{ dx }\) = \(\frac{\sec ^{2} x-y}{x+2 y-1}\).
Question 5.
x² + xy + y² = 100
Solution:
x² + xy + y² = 100
Differentiating w.r.t. x,
2x + (1.y + x. \(\frac { dy }{ dx }\)) + 2y \(\frac { dy }{ dx }\) = 0
or (x + 2y) \(\frac { dy }{ dx }\) = – 2x – y
∴ \(\frac { dy }{ dx }\) = – \(\frac{ 2x+y }{ x+2y }\).
Question 6.
x³ + x²y + xy² + y³ = 81
Solution:
x³ + x²y + xy² + y³ = 81
Differentiating w.r.t. x,
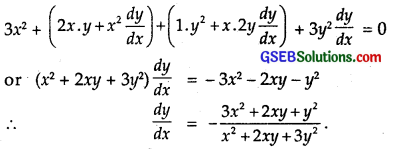
Question 7.
sin² y + cos xy = π
Solution:
sin² y + cos xy = π
Differentiating w.r.t. x,
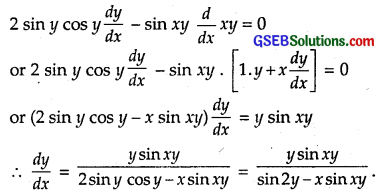
Question 8.
sin² x + cos² y = 1
Solution:
sin² x + cos² y = 1
Differentiating w.r.t. x,
2 sin x \(\frac { d }{ dx }\) (sin x) + 2 cosy \(\frac { d }{ dx }\) (cos y) = 0
or 2 sin x cos x + 2 cos y(- sin y) \(\frac { dy }{ dx }\) = 0
or 2sin x cos x – 2cos y sin y \(\frac { dy }{ dx }\) = 0
∴ \(\frac { dy }{ dx }\) = \(\frac { 2 sin x cos x}{ 2sin y cos y }\) = \(\frac { sin 2x }{ sin 2y }\).
Question 9.
y = sin-1\(\left(\frac{2 x}{1+x^{2}}\right)\)
Solution:
y = sin-1\(\left(\frac{2 x}{1+x^{2}}\right)\). put x = tanθ
So, y = sin-1\(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\) = sin-1(sin 2θ)
= 2θ = 2 tan-1x.
Question 10.
y = tan-1\(\frac { 2x }{ 2 }\)\(\frac{-1}{\sqrt{3}}\) < x < \(\frac{1}{\sqrt{3}}\)
Solution:
y = tan-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\). put x = tanθ
So, y = tan-1\(\left(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\right)\) = tan-1(tan 3θ)
= 3θ = 3 tan-1x.
∴ \(\frac { dy }{ dx }\) = \(\frac{3}{1+x^{2}}\)
Question 11.
y = cos-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\), 0 < x < 1
Solution:
y = cos-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\). put x = tanθ
So, y = cos-1\(\left(\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}\right)\) = cos-1(cos 2θ)
= 2θ = 2 tan-1x.
∴ \(\frac { dy }{ dx }\) = \(\frac{2}{1+x^{2}}\)
Question 12.
y = sin-1\(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), 0 < x < 1
Solution:
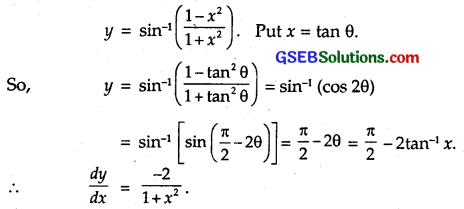
Question 13.
y = cos-1\(\left(\frac{2 x}{1+x^{2}}\right)\), – 1 < x < 1
Solution:

Question 14.
y = sin-1\(\left(2 x \sqrt{1-x^{2}}\right)\), – \(\frac{-1}{\sqrt{2}}\) < x < \(\frac{1}{\sqrt{2}}\)
Solution:
y = sin-1\(\left(2 x \sqrt{1-x^{2}}\right)\)Put x = sin θ.
y = sin-1(2sinθ\(\left.\sqrt{1-\sin ^{2} \theta}\right)\))
= sin-1(2 sin θ cos θ)
= sin-1(sin 2θ) = 2θ = 2 -1x.
∴ \(\frac { dy }{ dx }\) = \(\frac{2}{\sqrt{1-x^{2}}}\)
Question 15.
y = sec-1\(\left(\frac{1}{2 x^{2}-1}\right)\), 0 < x < \(\frac{1}{\sqrt{2}}\)
Solution:
y = sec-1\(\left(\frac{1}{2 x^{2}-1}\right)\)Put x = cos θ.
y = sec-1\(\left(\frac{1}{2 \cos ^{2} \theta-1}\right)\) = sec-1\(\frac{1}{cosθ}\)
= sec-1(sec 2θ) = θ = 2 cos-1x.
= sec-1(sec 2θ) = 2θ = 2cos-1x.
∴ \(\frac { dy }{ dx }\) = \(\frac{- 2}{\sqrt{1-x^{2}}}\)