GSEB Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.4

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.4 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.4

Question 1.
\(\frac{e^{x}}{\sin x}\)
Solution:
Let y = \(\frac{e^{x}}{\sin x}\).

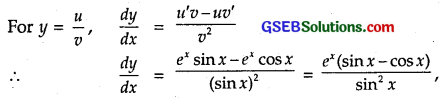
where x ≠ nπ, x ∈ Z.

Question 2.
\(e^{\sin ^{-1} x}\)
Solution:
Let y = \(e^{\sin ^{-1} x}\)
Put sin^-1x = t.
∴ y = e^t.

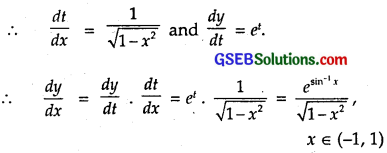
Question 3.
\(e^{x^{3}}\)
Solution:
Let y = \(e^{x^{3}}\). Put x³ = t.
∴ y = e^t and t = x³.
⇒ \(\frac { dy }{ dt }\) = e^t and \(\frac { dt }{ dx }\) = 3x².
∴ \(\frac { dy }{ dx }\) = \(\frac { dy }{ dt }\) x \(\frac { dt }{ dx }\) = e^t x 3x² = 3x²\(e^{x^{3}}\).

Question 4.
sin(tan^-1 e^-x)
Solution:
Let y = sin(tan^-1 e^-x)
Put y = sin s, s = tan^-1 t and t = e^-x

Question 5.
log (cos e^x)
Solution:
Let y = log (cos e^x).
Put y = log s, s = cos t and t = e^x.

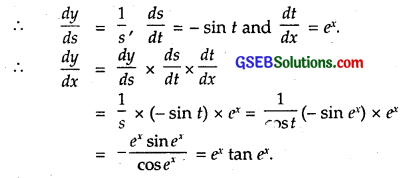
Question 6.
e^x + \(e^{x^{2}}\) + … + \(e^{x^{5}}\)
Solution:

Question 7.
\(\sqrt{e^{\sqrt{x}}}\), x > 0
Solution:
Let y = \(\sqrt{e^{\sqrt{x}}}\).
Put y = \(\sqrt{s}\), s = e^t and t = \(\sqrt{x}\).
Differentiating, we get

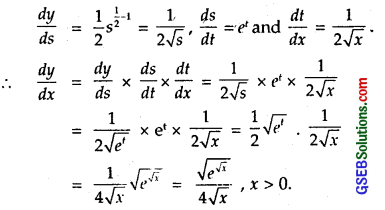
Question 8.
log log x, x > 1
Solution:
Let y = log(log x).
Put y = log t and t = log x.
Differentiating, we get
\(\frac { dy }{ dt }\) = \(\frac { 1 }{ t }\) and \(\frac { dt }{ dx }\) = \(\frac { 1 }{ x }\).
∴ \(\frac { dy }{ dx }\) = \(\frac { dy }{ dt }\) x \(\frac { dt }{ dx }\) = \(\frac { 1 }{ t }\) x \(\frac { 1 }{ x }\) = \(\frac { 1 }{ log x }\) . \(\frac { 1 }{ x }\)
= \(\frac { 1 }{ x log x }\), x > 0

Question 9.
\(\frac { cos x }{ log x }\), x > 0
Solution:
Let y = \(\frac { cos x }{ log x }\).

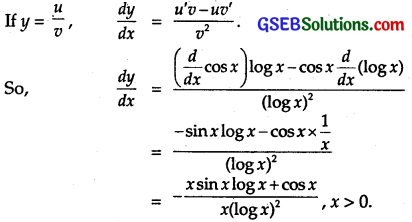
Question 10.
cos (log x + e^x), x > 0
Solution:
Let y = cos (log x + e^x)
Put y = cos t, t = log x + e^x
Differentiating, we get
\(\frac { dy }{ dx }\) = – sin t and \(\frac { dt }{ dx }\) = \(\frac { 1 }{ x }\) + e^x.
∴ \(\frac { dy }{ dx }\) = \(\frac { dy }{ dt }\) x \(\frac { dt }{ dx }\) = – sin t x ( \(\frac { 1 }{ x }\) x e^x).
= – sin (log x + ^x) x (\(\frac { 1 }{ x }\) + e^x)
= – \(\frac { 1 }{ x }\) (1 + xe^x) sin (log x + e^x).