Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.6 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.6
![]()
Question 1.
x = 2at², y = at4
Solution:
x = 2at², y = at4
So, \(\frac { dx }{ dt }\) = 4at, \(\frac { dy }{ dt }\) = 4at³.
∴ \(\frac { dy }{ dx }\) = \(\frac{\frac{d y}{d t}}{\frac{d x}{d t}}\) = \(\frac{4 a t^{3}}{4 a t}\) = t².
Question 2.
x = a cos θ, y = b cos θ .
Solution:
x = x = a cos θ, y = b cos θ .
So, \(\frac { dx }{ dθ }\) = – a sin θ, \(\frac { dy }{ dθ }\) = – b sin θ.
∴ \(\frac { dy }{ dx }\) = \(\frac{\frac{d y}{d θ}}{\frac{d x}{d θ}}\) = \(\frac{-b \sin \theta}{-a \sin \theta}\) = \(\frac { b }{ a }\).
![]()
Question 3.
x = sin t, y = cos 2t
Solution:
x = sin t, y = cos 2t
So, \(\frac { dx }{ dt }\) = cos t, \(\frac { dy }{ dt }\) = – 2 sin t = – 4 sin tcos t.
∴ \(\frac { dy }{ dx }\) = \(\frac{\frac{d y}{d t}}{\frac{d x}{d t}}\) = \(\frac{-4 \sin t \cos t}{\cos t}\) = – 4 sin t.
Question 4.
x = 4t, y = \(\frac { 4 }{ t }\)
Solution:
x = 4t, y = \(\frac { 4 }{ t }\)
∴ \(\frac { dx }{ dt }\) = 4, \(\frac { dy }{ dt }\) = \(\frac{-4}{t^{2}}\)
∴ \(\frac { dy }{ dx }\) = \(\frac{\frac{d y}{d t}}{\frac{d x}{d t}}\) = \(\frac{-4}{\frac{t^{2}}{4}}\) = – \(\frac{1}{t^{2}}\)
Question 5.
x = cos θ – cos 2θ, y = sin θ – sin 2θ.
Solution:
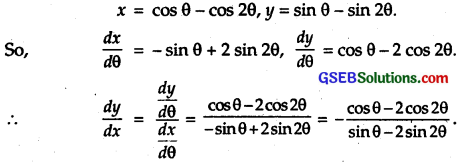
Question 6.
x = a(θ – sin θ), y = a(1 + cos θ).
Solution:
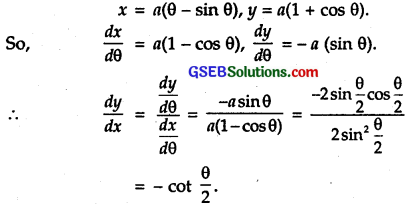
![]()
Question 7.
x = \(\frac{\sin ^{3} t}{\sqrt{\cos 2 t}}\), y = \(\frac{\cos ^{3} t}{\sqrt{\cos 2 t}}\)
Solution:

Question 8.
x = a[cos t + log tan\(\frac{t}{2}\), y = a sin t
Solution:
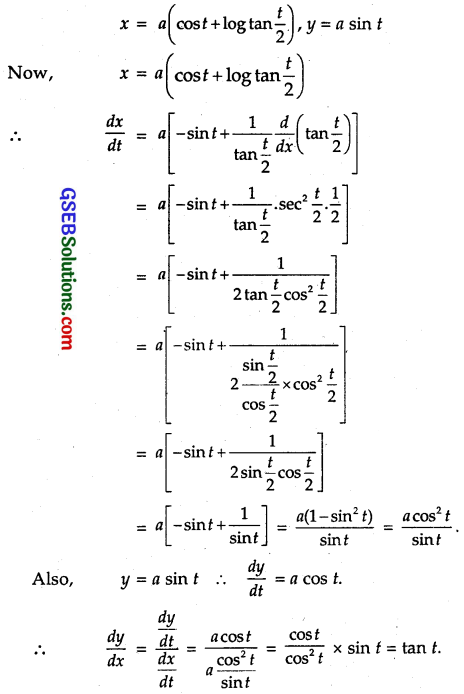
Question 9.
x = a sec θ, y = b tan θ
Solution:
x = a sec θ, y = b tan θ
So, \(\frac { dx }{ dθ }\) = a sec θ tan θ, \(\frac { dy }{ dθ }\) = b sin² θ.
∴ \(\frac { dy }{ dx }\) = \(\frac{\frac{d y}{d θ}}{\frac{d x}{d θ}}\) = \(\frac{b \sec ^{2} \theta}{a \sec \theta \tan \theta}\) = \(\frac { b }{ a }\) . \(\frac{1}{\cos \theta \frac{\sin \theta}{\cos \theta}}\)
= \(\frac { b }{ a }\)cosec θ.
![]()
Question 10.
x = a(cos θ + θ sin θ), y = a (sin θ – θ cos θ)
Solution:
So, \(\frac { dx }{ dθ }\) = a(- sin θ + 1 . sin θ + θ cos ) = a θ cos θ.
\(\frac { dy }{ dθ }\) = a(cos θ – 1. cos θ – θ . ( – sin θ)] = a θ sin θ
∴ \(\frac { dy }{ dθ }\) = \(\frac{\frac{d y}{d θ}}{\frac{d x}{d θ}}\) = \(\frac{a \theta \sin \theta}{a \theta \cos \theta}\) = tan θ.
Question 11.
If x = \(\sqrt{a^{\sin ^{-1} \cdot t}}\) and y = \(\sqrt{a^{\cos ^{-1} \cdot t}}\), show that \(\frac { dy }{ dx }\) =\(\frac { – y }{ x }\)
Solution:
