Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.8 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.8
![]()
Question 1.
Verify Rolle’s Theorem for the function f(x) = x² + 2x – 8, x ∈ [- 4, 2].
Solution:
Now, f(x) = x² + 2x – 8 is a polynomial. Therefore, it is continuous and derivable in its domain x ∈ R. Hence, it is continuous in the interval [- 4, 2] and derivable in the interval (- 4, 2).
f(- 4) = (- 4)² + 2(- 4) – 8 = 16 – 8 – 8 = 0
and f(2) = 2² + 4 – 8 = 8 – 8 = 0.
∴ Conditions of Rolle’s theorem are satisfied.
Now, f'(x) = 2x + 2
f'(c) = 2c + 2 = 0 or c = – 1.
Now, c = – 1 ∈ [- 4, 2]
Thus, f'(c) = 0 at c = – 1.
![]()
Question 2.
Examine if Rolle’s theorem is applicable to any of the following functions. Can you say something about the converse of Rolle’s theorem from these examples?
(i) f(x) = [x] for x ∈ [5, 9]
(ii) f(x) = [x] for x ∈ [- 2, 2]
(iii) f(x) = x² – 1 for x ∈ [1, 2]
Solution:
(i) In the interval [5, 9], f(x) = [x] is neither continuous nor derivable at x = 6,7,8.
Hence, Rolle’s theorem is not applicable.
(ii) f(x) = [x] is not continuous and derivable at – 1, 0, 1.
Hence, Rolle’s theorem is not applicable.
(iii) f(x) = (x² – 1), f(1) = 1 – 1 = 0, f(2) = 2² – 1 = 3
Thus, f(a) ≠ f(b).
Though it is continuous in the interval [1, 2] and derivable in the interval (1, 2), still Rolle’s Theorem is not applicable.
In case of converse, if f'(c) = 0, c ∈ [a, b], then conditions of Rolle’s theorem are not true.
(i) f(x) = [x] is the greatest integer less than or equal to x.
∴ f’ (x) = 0. But f is neither continuous in the interval [5, 9] nor differentiable in the interval (5, 9).
(ii) Here also, though f'(x) = 0, but fis neither continuous in interval [- 2, 2] nor differentiable in the interval (- 2, 2).
(iii) f(x) = x² – 1, f'(x) = 2x. Here f'(x) is not zero in the interval [1, 2]. So, f(2) ≠ f(1)
![]()
Question 3.
If f: [- 5, 5] → R is a differentiable function and if f’ (x) does not vanish anywhere, then prove that f(- 5) ≠ f(5).
Solution:
For Rolle’s theorem: If
(i) f is continuous in [a, b],
(ii) f is derivable in (a, b).
(iii) f(a) = f(b)
then f'(c) = 0, c ∈ (a, b)
We are given f is continuous and det
but f'(c) ≠ 0 ⇒ f(a)
i.e., f(-5) ≠ f(5).
Question 4.
Verify Mean Value Theorem for f(x) = x² – 4x – 3 in the interval [a, b], where a = 1, b = 4.
Solution:
f(x) = x² – 4x – 3. Being a polynomial, it is continuous in the interval [1, 4] and derivable in (1, 4).
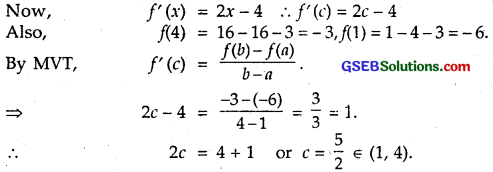
Question 5.
Verify Mean Value Theorem for f(x) = x³ – 5x² – 3x in the interval [a, b], where a = 1, b = 3. Find all c ∈ (1,3) for which f'(c) = 0.
Solution:
f(x) = x³ – 5x² – 3x.
It is a polynomial. Therefore, it is continuous in the interval [1, 3] and derivable in the interval (1, 3).

None of these values ∈ (1, 3).
![]()
Question 6.
Examine the applicability of Mean Value Theorem for all the three functions given in the question 2.
Solution:
(i) f(x) = [x] for x ∈ [5, 9],
f(x) = [x] is neither continuous in the interval [5, 9] nor differentiable in the interval (5, 9).
Hence, MVT is not applicable.
(ii) f(x) = [x], for x ∈ [- 2, 2].
Again f(x) = [x] is neither continuous in the
interval [- 2, 2] nor differentiable in the interval (- 2, 2).
Hence, MVT is not applicable.
(iii) f(x) = x² – 1 for x ∈ [1, 2].
It is a polynomial. Therefore, it is continuous in the interval [1, 2] and differentiable in the interval (1, 2).
∴ f’ (x) = 2x, f(1) = 1 – 1 = 0, f(2) = 4 – 1 = 3.
∴ f'(c) = 2c.
By MVT, f'(c) = \(\frac { f(b) – f(c) }{ b-a }\)
2c = \(\frac { 3-0 }{ 2-1 }\)
∴ c = \(\frac { 3 }{ 2 }\), which belongs to (1, 3).
![]()