Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.5
![]()
Question 1.
Find the maximum and minimum values, if any, of the following functions given by
(i) f(x) = (2x – 1)² + 3
(ii) f(x) = 9x² + 12x + 2
(iii) f(x) = – (x -1)² + 10
(iv) g(x) = x³ + 1
Solution:
(i) Minimum value of (2x – 1)² is zero.
∴ Minimum value of (2x – 1)² + 3 is 3.
There is no finite maximum value.
(ii) f(x) = 9x² + 12x + 2
= (3x + 2)² – 2
Minimum value of (3x + 2)² is zero.
∴ Minimum value of (3x + 2)² – 2 = 9x² + 12x + 2 is – 2.
f(x) does not have any finite maximum value.
(iii) f(x) = – (x- 1)² + 10
Maximum value of – (x – 1)² is zero
∴ Maximum value of f(x) = – (x – 1)² + 10 is 10.
f(x) does not have any finite minimum value.
(iv) f(x) = x³ + 1
As x → ∞, f(x) → ∞.
As x → – ∞, f(x) → – ∞.
Moreover, f(x) = 3x² + 1 = +ve for all x → R.
∴ f(x) is an increasing function throughout its domain.
Hence, there is no maximum and minimum values.
![]()
Question 2.
Find the maximum and minimum values, if any, of the following functions given, by
(i) f(x) = |x + 2| – 1
(ii) g(x) = -|x + 1| + 3
(iii) h(x) = sin (2x) + 5
(iv) f(x) = | sin 4x + 3 |
(v) h(x) = x + 1, x ∈ (-1,1)
Solution:
(i) | x + 2 | > 0, x ∈ R,
f(x) = [x + 2] – 1 > – 1
Minimum value of f(x) is – 1. There is no maximum value.
(ii) Let g(x) = – | x + 1| + 3.
Now, [x + 1] ≥ 0 for all x ∈ R.
⇒ – [x + 1] ≤ 0 for all x ∈ R.
– [x + 1] + 3 ≤ 3 ⇒ g(x) < 3.
Thus, the maximum value of f(x) is 3, there is no minimum value.
(iii) Let f(x) = sin 2x + 5.
Maximum value of sin 2x is 1.
Maximum value of sin 2x + 5 = 1 + 5 = 6.
Minimum value of sin 2x is – 1.
∴ Minimum value of ski 2x + 5 = – 1 + 5 = 4.
(iv) Let fix) = [sin 4x + 3].
Maximum value of sin 4x is 1.
∴ Maximum value of [sin 4x + 3] is [1 + 3] = 4.
Minimum value of sin 4x is – 1.
∴ Minimum value of fix) is [-1 + 3] = [2] = 2.
(v) Let h(x) = x + 1.
As x → ∞, h(x) → ∞.
Also, x → – ∞, h(x) → – ∞.
Thus, there is no maximum or minimum value.
However, at x = 1, h(x) = 1 + 1 = 2
and at x = -1, h(x) = -1 + 1 = 0.
∴ Greatest value of h(x) is 2 and least value is 0.
![]()
Question 3.
Find the local maxima or local minima, if any, of the following functions. Find also the local maximum and local minimum values, as the case may be :
(i) f(x) = x²
(ii) g(x) = x³ – 3x
(iii) h(x) = sin x + cos x, 0 < x < \(\frac { π }{ 2 }\)
(iv) f(x) = sin x – cos x, 0 < x < 2π (v) f(x) = x³ – 6x² + 9x + 15 (vi) g(x)= \(\frac { x }{ 2 }\) + \(\frac { 2 }{ x }\), x> 0
(vii) g(x) = \(\frac{1}{x^{2}+2}\)
(viii) f(x) = x\(\sqrt{1-x}\), x > 0
Solution:
(i) Let f(x) = x² ⇒ f'(x) = 2x.
Now, f'(x) = 0 ⇒ 2x = 0
i.e., x = 0.
At x = 0 :
When x is slightly < 0, f'(x) is – ve. When x is slightly > 0,f'(x) is + ve.
∴ f'(x) changes sign from – ve to + ve as x increases through 0.
⇒ f(x) has a local minima at x = 0.
Local minimum valus = f(0) = 0.
(ii) Let g(x) = x³ – 3x
∴ g'(x) = 3x² – 3 = 3(x²-1) = 3(x-1)(x+1)
Now, g’ (x) = 0
⇒ 3(x-1)(x+1) = 0
⇒ Either x = 1 or x = – 1.
At x = 1:
When x is slightly < 1, g’(x) is (+)(-)(+), i..e, – ve. When x is slightly > 1, g'(x) is (+)(+)(+), i.e.,+ve.
Thus g'(x) changes sign from negative to positive as x increases through 1 and hence x = 1 is a point of local minima.
At x = – 1:
When x is slightly < – 1, g'(x) is (+)(-)(-), i.e., +ve. When x is slightly > – 1, g'(x) is (+)(-)(+), i.e. -ve.
Thus g'(x) changes sign from positive to negative as x increases through -1 and hence x = -1 is a point of local maxima.
Local minimum value = f(1) = 1 – 3 = – 2.
Local maximum value = f(- 1) = – 1 + 3 = 2.
(iii) h(x) = sin x + cos x
∴ h’(x) =cos x – sin x
= cos x(1 – tan x)
h’(x) = 0
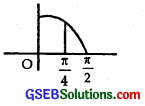
⇒ cos x – sin x = 0.
or tan x = 1 ⇒ x = \(\frac { π }{ 4 }\).
x = \(\frac { π }{ 4 }\) ∈ (0, \(\frac { π }{ 2 }\)).
At x = \(\frac { π }{ 4 }\), h’(x) = cos x (1 – tan x) = 0
When x is slightly < \(\frac { π }{ 4 }\),
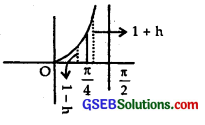
cos x = + ve
and tan x = 1 – h,
where h is small.
So, 1 – tan x = 1 – (1 – h) = + ve.
⇒ h’(x) = cos x (1 – tan x) = (+)(+) = +ve.
When x is slightly > \(\frac { π }{ 4 }\),
cos x = + ve
and tan x = 1 + h, where h is small
∴ 1 – tan x = 1 – (1 + h) = – h = – ve.
∴ h’(x) = cos x(1 – tan x) = (+)(-) = – ve.
Hence, there is a local maxima at x = \(\frac { π }{ 4 }\)
Local maximum value = h\(\frac { π }{ 4 }\) = sin \(\frac { π }{ 4 }\) + cos \(\frac { π }{ 4 }\)
= \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\) = \(\frac{2}{\sqrt{2}}\) = \(\sqrt{2}\).
(iv) f(x) = sin x – cos x, 0 < x < 2π
f’(x) = cos x + sin x = cos x(1 + tan x)
f’(x) = 0
⇒ cos x + sin x = 0 = tan x = – 1.
∴ x = \(\frac { 3π }{ 4 }\), \(\frac { 7π }{ 4 }\)
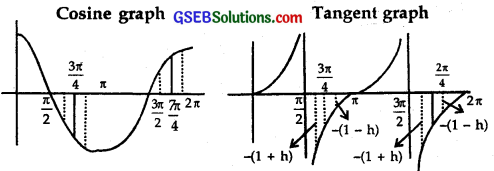
At x = \(\frac { 3π }{ 4 }\)
(a) When x is slightly < \(\frac { 3π }{ 4 }\),
cos x = – ve, tan x = – (1+h) = – 1 – h
∴ 1 + tan x = 1 + (- 1 – h) = – h = + ve
(b) When x is slightly < \(\frac { 3π }{ 4 }\),
cos x = – ve, tan x = – (1+h) = – 1 – h
∴ 1 + tan x = 1 + (- 1 – h) = – h = + ve
∴ f'(x) = cos x (1 + tan x) = (-)(+) = – ve.
∴ f'(x) changes sign from +ve to – ve
∴ At x = \(\frac { 3π }{ 4 }\), there is point pf local maxima.
Local maximum value
= f (\(\frac { 3π }{ 4 }\)) = sin \(\frac { 3π }{ 4 }\) – cos \(\frac { 3π }{ 4 }\)
= \(\frac{1}{\sqrt{2}}\) + \(\frac{1}{\sqrt{2}}\) = \(\frac{2}{\sqrt{2}}\) = \(\sqrt{2}\).
At x = \(\frac { 7π }{ 4 }\),
(a) When x is slightly < \(\frac { 7π }{ 4 }\), cos x = – ve, tan x = – (1+h) ⇒ 1 + tan x = 1 – (1+h) = – h ∴ f'(x) = cos x (1 + tan x) = (-)(+) = – ve. (b) When x is slightly > \(\frac { 7π }{ 4 }\),
cos x = – ve, tan x = – (1+h) ⇒ 1 + tan x = 1 – (1 + h) = – h
∴ f'(x) = cos x (1 + tan x) = (-)(+) = – ve.
∴ f'(x) changes sign from – ve to + ve.
Hence, there is a local minima at x = \(\frac { 7π }{ 4 }\).
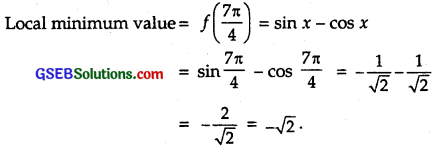
(v) Let f(x) = x³- 6x² + 9x + 15
f(x) = 3x² -12x + 9 = 3(x² – 4x + 3)
= 3(x – 1)(x – 3).
Now, f(x) = 0 ⇒ x = 1, 3.
At x = 1:
When x is slightly < 1, f(x) = (-)(-) = +ve. When x is slightly > 1, f(x) = (+)(-) = -ve.
∴ f'(x) changes sign from +ve to -ve as x increases through 1.
⇒ f(x) has a local maxima at x = 1.
Local maximum value = f( 1) = 1 – 6 + 9 + 15 = 19.
At x = 3 :
When x is slightly < 3, fix) = (+)(-) = -ve. When x is slightly > 3, f\x) = (+)(+) = +ve.
f'(x) changes sign from -ve to +ve as x increases through 3.
⇒ f(x) has a local minima at x = 3.
∴ Local minimum value
= f(3) = (3)³ – 6(3)² + 9(3) + 15
= 27-54 + 27 + 15 = 15.
[Note : How to determine the change of sign of f(x) as x increases through a particular point?
Let f’ (x) = (x – a)(x – b)(x – c)
At x = a, x – a = a – a = 0, x – b = a – b, x – c = a – c.
Sign corresponding to x – a changes from -ve to +ve, sign responding to x – b is that of a – b and remains the same.
Sign corresponding to x – c is that of a – c and remains the same.
Let f'(x) = (x – 1)(x – 3)
At x = 1, x – 1 = 1 – 1 = 0, x – 3 = 1 – 3 = – 2 = – ve
Factor (x – 1)(x – 3)
Signs when x is slightly < 1 are (-)(-) = +ve. Signs when x is slightly > 1 are : (+)(-) = -ve
∴ f'(x) changes from +ve to -ve
At x = 3, x – 1 = 3 – 1 = 2 = +ve, x – 3 = 3 – 3 = 0
Factor (x-1)(x-3)
Sign when x is slightly < 3, (+)(-) = -ve Sign when x is slightly > 3, (+)(+) = +ve
∴ f(x) changes sign from -ve to +ve
(vi)
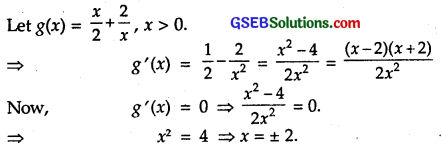
Since it is given that x > 0, hence x = – 2 is rejected.
For x slightly < 2, g'(x)= \(\frac{(-)(+)}{(+)}\) = – ve. For x slightly > 2, g ‘(x) = \(\frac{(+)(+)}{(+)}\) = +ve.
Thus, g'(x) changes sign from -ve to +ve.
Hence, g(x) has a local minima at x = 2.
Local minimum value = g(x) = \(\frac { 2 }{ 2 }\) + \(\frac { 2 }{ 2 }\) = 1 + 1 = 2.
(vii) Let g(x) = \(\frac{1}{x^{2}+2}\)
∴ g'(x) = – \(\frac{2 x}{\left(x^{2}+2\right)^{2}}\)
Now, g'(x) = 0 ⇒ x = 0
At x = 0 :
When x is slightly < 0, g'(x) = \(\frac{(-)(-)}{(+)}\) = + ve. When x is slightly > 0, g'(x) = \(\frac{(-)(+)}{(+)}\) = – ve.
∴ g'(x) changes sign from – ve to + ve as x increases through 0.
⇒ f(x) has a local minima at x = 0.
Local minimum valus = g(0) = \(\frac { 1 }{ 2 }\).
(viii)

When x is slightly < \(\frac { 2 }{ 3 }\) f(x) = \(\frac { (-)(-) }{ (+) }\) = + ve. When x is slightly > \(\frac { 2 }{ 3 }\)
f'(x) = \(\frac { (-)(+) }{ (+) }\) = – ve.
∴ f'(x) changes sign from +ve to -ve as x increases through x = \(\frac { 2 }{ 3 }\)
∴ f(x) has a local maxima at x = \(\frac { 2 }{ 3 }\).
Local maximum value = f(\(\frac { 2 }{ 3 }\)) = \(\frac { 2 }{ 3 }\)\(\sqrt{1-\frac{2}{3}}\) = \(\frac { 2 }{ 3 }\) . \(\frac{1}{\sqrt{3}}\) = \(\frac{2 \sqrt{3}}{9}\)
![]()
Question 4.
Prove that the following functions do not have maxima or minima :
(i) f(x) = ex
(ii) g(x) = log x
(iii) h(x) = x³ + x² + x + 1
Solution:
(i) f(x) = ex ⇒ f'(x) = ex.
For maxima and minima, f'(x) = 0.
⇒ ex = 0,
which is not defined for any finite value. Hence f'(x) = ex does not have maxima and minima.
(ii) We have : g(x) = log x.
∴ g'(x) = \(\frac { 1 }{ x }\).
Now, g'(x) = 0 ⇒ \(\frac { 1 }{ x }\) = 0,
which is not defined for any real x.
Hence, g(x) = log x does not have maxima and minima.
(iii) We have: h(x) = x³ + x² + x + 1.
h'(x) = 3x² + 2x + 1
Now, h'(x) = 0
⇒ 3x² + 2x + 1 =0
⇒ x = \(\frac{-2 \pm \sqrt{4-12}}{6}\) = \(\frac{-1 \pm \sqrt{-2}}{3}\)
i.e., h'(x) = 0 at imaginary points.
i.e., h'(x) ≠ 0 for any real value of x.
Hence, there is neither maximum nor minimum.
Question 5.
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:
(i) f(x) = x³[-2, 2]
(ii) f(x) = sin x + cos x, x ∈ [0, π]
(iii) f(x) = 4x – x², x ∈ [-2, \(\frac { 9 }{ 2 }\)]
(iv) f(x) = (x – 1)² + 3, x ∈ [-3, 1]
Solution:
(i) We have: f(x) = x³ in [- 2, 2].
∴ f'(x) = 3x²
Now, f'(x) = 0 at x = 0, f(0) = 0.
Now, f(- 2) = (-2)³ = – 8;
f(0) = (0)³ = 0
and f(2) = (2)³ = 8
Hence, the absolute maximum value of f(x) is 8, which is attained at x = 2 and absolute minimum value of f(x) = – 8, which is attained at x = – 2.
(ii) We have :
f(x) = sin x + cos x in [0, π].
∴ f'(x) = cos x – sin x
For extreme values, f'(x) = 0.
⇒ cos x – sin x = 0 ⇒ 1 – tan x = 0
⇒ tan x = 1 ⇒ x = \(\frac { π }{ 4 }\).
Now, we find f(x) at x = 0, \(\frac { π }{ 4 }\) and π.
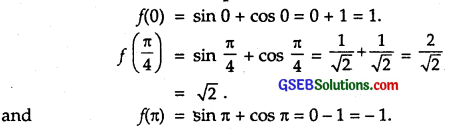
∴ Absolute maximum value = \(\sqrt{2}\) at x = \(\frac { π }{ 4 }\)
and absolute minimum value = 3 at x = π.
(iii)
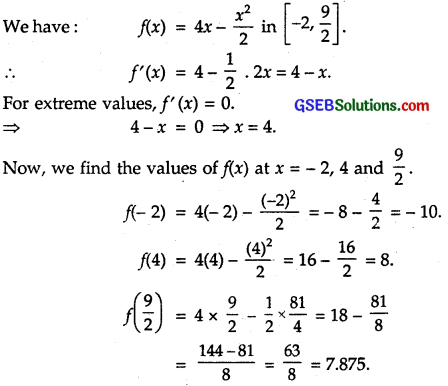
At x = 4, absolute maximum value = 8.
At x = – 2, absolute minimum value = – 10.
(iv) We have : f(x) = (x – 1)² + 3 in [- 3,1].
∴ f'(x)= 2(x-1).
For extreme values, f'(x) = 0.
⇒ 2(x-1) = 0 ⇒ x – 1 = 0 ⇒ x = 1.
Now, we find f(x) at x = 1 and – 3.
f(1) = (1-1)² + 3 = 0 + 3 = 3.
f(-3) = (- 3 – 1)² + 3 = 16 + 3 = 19.
![]()
Question 6.
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 – 24x -18².
Solution:
Profit function is p(x) = 41 – 24x – 18x².
∴ p'(x) = – 24 – 36x = – 12(2 + 3x)
For maxima and minima,
p'(x) = 0.
Now, p'(x) = 0 ⇒ – 12(2 + 3x) = 0.
⇒ 2 + 3x = 0 ⇒ x = – \(\frac { 2 }{ 3 }\)
p’(x) changes sign from +ve to -ve as it passes through – \(\frac { 2 }{ 3 }\)
⇒ p(x) has a maximum value at x = – \(\frac { 2 }{ 3 }\).
∴ Maximum profit = p\(\frac { 2 }{ 3 }\)
= 41 – 24(-\(\frac { 2 }{ 3 }\)) – 18(-\(\frac { 2 }{ 3 }\))²
= 41 + 16-8 = 49.
Question 7.
Find both the maximum and minimum values of 3x4 – 8x³ + 12x² – 48x + 25 on the interval [0, 3].
Solution:
Let f(x) = 3x4 – 8x³ + 12x² – 48x + 25.
∴ f'(x) = 12x³ – 24x² + 24x – 48
= 12(x³ – 2x² + 2x – 4)
= 12[x²(x – 2) + 2(x – 2)]
= 12(x² + 2)(x – 2)
For maxima and minima,
f'(x) = 0.
⇒ 12(x² + 2)(x – 2) = 0
⇒ x = 2.
Now, we find f(x) at x = 0, 2 and 3.
f(0) = 25,
f(2) = 3(2)4 – 8(2)³ + 12(2)² – 48(2) + 25
= 48 – 64 + 48 – 96 + 25 = – 39.
and f(3) = 3(3)4 – 8(3)³ + 12(3)2 – 48(3) + 25
= 243 – 216 + 108 -144 + 25 = 16.
Hence, at x = 0, maximum value = 25,
and at x = 2, minimum value = – 39.
Question 8.
At what points in the interval [0, 2π], does the function sin 2x attains its maximum value?
Solution:
We have : f(x) = sin 2x in [0, 2π].
∴ f’ (x) = 2 cos 2x.
For maxima and minima f'(x) = 0.
⇒ 2 cos 2x = 0 ⇒ cos 2x = 0
⇒ 2x = \(\frac { π }{ 2 }\), \(\frac { 3π }{ 2 }\), \(\frac { 5π }{ 2 }\), \(\frac { 7π }{ 2 }\)
x = \(\frac { π }{ 4 }\), \(\frac { 3π }{ 4 }\), \(\frac { 5π }{ 4 }\), \(\frac { 7π }{ 4 }\).
Now, we find f(x) at x = 0, \(\frac { π }{ 4 }\), \(\frac { 3π }{ 4 }\), \(\frac { 5π }{ 4 }\), \(\frac { 7π }{ 4 }\) and 2π.
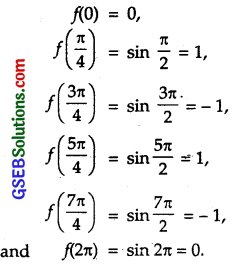
Hence, maximum value of f(x) = 1 is at x = \(\frac { π }{ 4 }\) and x = \(\frac { 5π }{ 4 }\).
Question 9.
What is the maximum value of the function sin x + cos x?
Solution:
Consider the interval [0, 2π].
Let f(x) = sin x + cos x.
⇒ f'(x) – cos x – sin x. ,
For maxima and minima,
f'(x) = 0
⇒ cos x- sin x = 0 ⇒ tan x = 1.
⇒ x = \(\frac { π }{ 4 }\) and \(\frac { 5π }{ 4 }\)
Now, we find f(x) at x = 0, \(\frac { π }{ 4 }\), \(\frac { 5π }{ 4 }\) and 2π.

Hence, maximum value of f(x) = \(\sqrt{2}\)
Question 10.
Find the maximum value of 2x³ – 24x +107 in the interval [1, 3]. Find the maximum value of the same function in [- 3, -1].
Solution:
We have : f(x) = 2x³ – 24x + 107 in [1, 3].
f'(x) = 6x² – 24.
For maxima and minima,
f'(x) = 0.
⇒ 6x² – 24 = 0 ⇒ x = ± 2.
For the interval [1, 3], we find the values of f(x) at x = 1, 2, 3
f(1) = 2(1)³ – 24 x 1 + 107 = 85,
f(2) = 2(2)³ – 24 x 2 + 107 = 75
and
f(3) = 2(3)³ – 24 x 3 + 107 = 89.
Hence, maximum value of f(x) = 89 at x = 3.
For the interval [- 3,-1], we find the values off(x) at x = – 3, – 2 and – 1.
f(- 3) = 2(- 3)³ – 24 (- 3) + 107 = 125,
f(- 2) = 2(- 2)³ – 24 (- 2) + 107 = 139
and f(-1) = 2(-1)³ – 24 (-1) + 107 = 129.
Hence, maximum value of f(x) = 139 at x = – 2.
![]()
Question 11.
It is given that at x – 1, the function x4 – 62x² + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Solution:
We have: f(x) = x4 – 62x² + ax + 9.
∴ f'(x) = 4x³ – 124x + a.
Now, f'(x) = 0 at x = 1 [Given]
∴ f'(1) = 4 – 124 + a = 0
⇒ a = 120.
Now, f”(x) = 12x² – 124
At x = 1 : f”(1) = 12 – 124 = – 112 < 0.
⇒ f(x) has a maximum at x = 1, when a = 120.
Hence, a = 120.
Question 12.
Find the maximum and minimum values of x + sin 2x on [0,2 π].
Solution:
We have: f(x) = x + sin 2x on [0, π].
f'(x) = 1 + 2 cos 2x.
For maxima and minima,
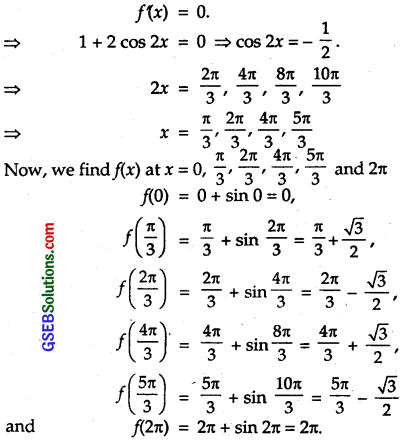
Hence, maximum value of f(x) = 2π
and minimum value of f(x) = 0.
Question 13.
Find two numbers whose sum is 24 and whose product is as large as possible.
Solution:
Let the required numbers be x and (24 – x).
Their product P = x(24 -x) = 24x – x².
Now, \(\frac { dp }{ dx }\) = 0 ⇒ 24 – 2x = 0
⇒ x = 12.
Also, \(\frac{d^{2} P}{d x^{2}}\) = – 2 < 0.
⇒ P is maximum at x = 12.
Hence, the required numbers are 12 and (24 -12), i.e., 12.
Question 14.
Find two positive numbers x and y such that x + y = 60 and xy³ is maximum.
Solution:

The value x = 60 is rejected as it makes y = 0.
At x = 15 :
When x is slightly < 15, \(\frac { dp }{ dx }\) = (+)(+) = +ve. When x is slightly > 15, \(\frac { dp }{ dx }\) = (+)(-) = -ve.
⇒ \(\frac { dp }{ dx }\) changes sign from +ve to -ve as x increases through 15.
∴ P is maximum at x = 15.
Hence, the required numbers are 15 and (60 – 15), i.e., 45.
![]()
Question 15.
Find two positive numbers x and y such that their sum is 35 and the product x²y5 is a maximum.
Solution:
We have : x + y = 35
⇒ y = 35 – x … (1)
So, product: P = x²5 – x²(35 – x)5 [Using (1)]
∴ \(\frac { dp }{ dx }\) = x².5(35 – x)4(-1) + (35 – x)5.2x
= x(35-x)4[-5x + 2(35-x)]
= x(35 – x)4 (70 – 7x)
Now, \(\frac { dp }{ dx }\) = 0.
⇒ x(35 – x)4(70 – 7x) = 0.
⇒ x = 0, 10, 35.
Only admissible values is x = 10 as x = 0 and 35 are rejected.
At x = 10:
When x is slightly < 10, \(\frac { dp }{ dx }\) = (+)(+)(+) = +ve. When x is slightly > 10, \(\frac { dp }{ dx }\) = (+)(+)(-)= -ve.
⇒ \(\frac { dp }{ dx }\) changes sign from + veto-ve as x increases through 10.
⇒ P is maximum at x = 10.
From (1), y = 35 -10 = 25.
Hence, the required numbers are 10 and 25.
Question 16.
Find two positive numbers whose sum is 16 and sum of whose cubes is minimum.
Solution:
Let two numbers be x and 16 – x.

Hence, the required numbers are 8 and (16-8), i.e., 8.
Question 17.
A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box ¡s the maximum possible?
Solution:
Let each side of the square lo be cut off be x cm.
∴ For the box:

Volume is maximum, when x = 3,
i.e., square of side = 3 cm is cut from each comer.
Question 18.
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cuttting off square from each comer and folding up flaps. What should be the side of the square to be cut off so that the volume of the box is maximum possible?
Solution:
Let each side of the square cut off from each comer be x cm.
∴ Sides of the rectangular box are (45 – 2x), (24 – 2x) and x cm.
Then, volume V of the box is given by

∴ V is maximum at x = 5, i.e., square of side 5 cm is cut off from each comer.
![]()
Question 19.
Show that the rectangle of maximum perimeter which can be inscribed in a circle of radius a is a square side \(\sqrt{2}\)a.
Solution:
Let the length and breadth of the rectangle inscribed in a circle of radius a be x and y respectively.
∴ x² + y² = (2a)²
⇒ x² + y² = 4a² … (1)
∴ Perimeter = 2(x + y).

For P(x) to be maximum, P'(x) = 0 and P”(x) < 0.
From (2), P'(x) = 0.

From (1), y² = 4a² – x²
= 4a² – 2a² = 2a² ⇒ y = \(\sqrt{2}\) a
Thus, x = y.
Hence, the rectangle is a square of side \(\sqrt{2}\) a.
Question 20.
Show that the right circular cylinder of the given surface area and maximum volume is such that its height is equal to the diameter of the base.
Solution:
Let S be the given surface area of the circular cylinder whose radius is r and height h. Let V be the its volume. Then,
Surface area S = 2πr² + 2πrh

∴ V is maximum.
Thus, volume is maximum, when h = 2r, i.e., when height of the cylinder = diameter of the base.
Question 21.
Of all the closed cylindrical cans (right circular cylinders) of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area.
Solution:
Let r be the radius and h be the height of cylindrical can.
∴ Volume = πr²h = 100 cm³.
∴ h = \(\frac{100}{\pi r^{2}}\)
Now, total surface area of the can

⇒ S is minimum or least, when r = \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\).
Hence, the total surface area is least when radius of base is \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) can and h = \(\frac{100}{\pi r^{2}}\) = \(\frac { 100 }{ π }\)\(\left(\frac{\pi}{50}\right)^{\frac{2}{3}}\) cm.
![]()
Question 22.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the lengths of the two pieces so that the combined area of the square and the circle is minimum?
Solution:
Let one part be of length x, then the other part will be 28-x.
Let the part of the length x be convetred into a circle of radius r.
∴ 2πr = x ⇒ r = \(\frac { x }{ 2π }\)
∴ Area of circle = πr² = π = \(\frac{x^{2}}{4 \pi^{2}}\) = \(\frac{x^{2}}{4 \pi}\)
Now second part of length 28 – x is converted into a square.

Differentiating (1) w.r.t. x, we get
\(\frac{d^{2} A}{d x^{2}}\) = \(\frac { 1 }{ 2π }\) + \(\frac { 1 }{ 8 }\)
⇒ A is minimum.
So, the two parts are x = \(\frac { 28π }{ 4+π }\) and 28 – x = \(\frac { 112 }{ 4+π }\)
Question 23.
Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is \(\frac { 8 }{ 27 }\) of the volume of the sphere.
Solution:
Let a cone VAB of greatest volume be inscribed in the sphere. Let ∠AOC = θ.
∴ Radius AC of the base of the cone v
= R sin θ
and VC = VO + OC
= R + R cos θ
= height of the cone.
∴ V, the volume of the cone

For maximum and minimum, we have : \(\frac { dv }{ dθ }\) = 0.
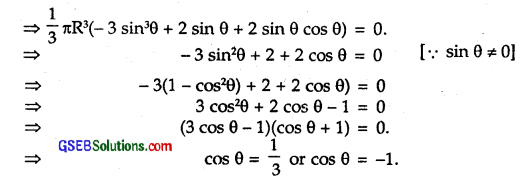
But cos θ ≠ – 1 as cos θ = – 1 ⇒ θ = π, which is not possible.

When θ is slightly < cos-1\(\frac { 1 }{ 3}\)
sin θ = +ve
3 cos θ – 1 = +ve [as θ decreases, cos θ increases)
and cos θ + 1 = +ve
∴ \(\frac { dv }{ dθ }\) = (+)(+)(+) = +ve.
When θ is slightly > cos-1\(\frac { 1 }{ 3}\)
sin θ = +ve, 3 cos θ – 1 = – ve and cosθ+ 1 = +ve.
[Since as θ increases, the value of cos θ decreases]
∴ \(\frac { dv }{ dθ }\) = (+)(-)(+) = – ve.
Thus, changes sign from +ve to —ve, when passes thorough cos-1\(\frac { 1 }{ 3}\).
Hence, V is maximum at θ = cos-1\(\frac { 1 }{ 3}\).
Now, maximum volume of cone

Question 24.
Show that the right circular cone of least curved surface area and given volume has an altitude equal to \(\sqrt{2}\) times the radius of the base.
Solution:
Let r and h be the radius and height of the cone respectively.

Also, \(\frac { dS }{dr}\). changes sign from -ve to +ve as r increases through the point k² = 2r6.
⇒ S is least at this point.
From (1), k² = h²4
⇒ h²4= 2r6 or h² = 2r².
∴ h = \(\sqrt{2}\)r.
![]()
Question 25.
Show that the semi-vertical angle of the cone of maximum volume and of given slant height is tan-1\(\sqrt{2}\).
Solution:
Let V be the volume, l be the slant height and 0 be the semi-vertical angle of the cone.
Now, volume V of the cone = \(\frac { 1 }{ 3}\)πr²h,
vertical height h = l cos θ
and radius r = l sin θ.

When θ is slightly < tan-1\(\sqrt{2}\)
sin θ cos²θ = + ve, tanθ – \(\sqrt{2}\) = – ve, tan θ + \(\sqrt{2}\) = + ve
∴ \(\frac { dv }{ dθ }\) = (-)(+)(-)(+) = +ve.
When θ is slightly > tan-1\(\sqrt{2}\)
sin θ cos² θ = +ve, tan θ – \(\sqrt{2}\) = +ve, tan θ + \(\sqrt{2}\) = +ve
∴ \(\frac { dv }{ dθ }\) = (-)(+)(+)(+) = – ve.
∴ \(\frac { dv }{ dθ }\) changes sign from +ve to – ve, when θ increases through tan-1\(\sqrt{2}\)
∴ V is maximum at θ = tan-1\(\sqrt{2}\).
Question 26.
Show that semi-vertical angle of a right circular cone of given surface area and maximum volume is sin-1\(\frac { 1 }{ 3}\).
Solution:
Let r be the radius, l be the slant height and h be the vertical height of a cone of semi- vertical angle CL.
∴ Surface area S = πrl + πr² … (1)
or l = \(\frac{S-\pi r^{2}}{\pi r}\).
The volume of the cone

Now \(\frac{d V^{2}}{d r}\) = 0 for maximum or minimum of V.
⇒ \(\frac { S }{ 9 }\)(2Sr – 8πr³) = 0 or S – 4π³ = S = 4π².
Putting S = 4πr² in (2), we get
\(\frac{d^{2} V^{2}}{d r^{2}}\) = \(\frac { S }{ 9 }\) [8πr² – 24πr²] = – ve.
⇒ V is maximum, when S = 4π².
Putting this value of S in (1), we get
4π² = πrl + πr².
or 3πr² = πrl.
or \(\frac { r }{ l }\) = sin α = \(\frac { 1 }{ 3 }\)
∴ l = sin-1\(\frac { 1 }{ 3}\).
Thus, for a given surface area, V is maxi*ium, when
α = sin-1\(\frac { 1 }{ 3}\).
![]()
Question 27.
The point on the curve x² = 2y which is nearest to the point (0, 5) is ______.
(A) (2\(\sqrt{2}\), 4)
(B) (2\(\sqrt{2}\), 0)
(C) (0, 0)
(D) (2, 2)
Solution:
Let P(x, y) be a point on the curve x² = 2y.
The other point is A(0,5)

⇒ Z is minimum at (2\(\sqrt{2}\), 4).
⇒ \(\sqrt{Z}\) is minimum at (2\(\sqrt{2}\), 4).
∴ Part (A) is the correct answer.
Question 28.
For all real values of x, the minimum value of \(\frac{1-x+x^{2}}{1+x+x^{2}}\) is ______.
(A) 0
(B) 1
(C) 3
(D) \(\frac { 1 }{ 3 }\)
Solution:

Question 29.
The maximum value of [x(x-1)+1]\(\frac { 1 }{ 3 }\), 0 ≤ x ≤ 1 is
(A) (\(\frac { 1 }{ 3 }\))\(\frac { 1 }{ 3 }\)
(B) \(\frac { 1 }{ 2 }\)
(C) 1
(D) \(\frac { 1 }{ 3 }\)
Solution:
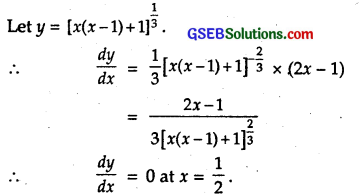
Also, \(\frac { dy }{ dx }\) changes sign from – ve to + ve at x = \(\frac { 1 }{ 2 }\),
∴ y is miniinum at x = \(\frac { 1 }{ 2 }\)
Value of y at x= 0, (0 + 1)\(\frac { 1 }{ 3 }\) = 1\(\frac { 1 }{ 3 }\) = 1,
Value of y at x= 1, (0 + 1)\(\frac { 1 }{ 3 }\) = 1\(\frac { 1 }{ 3 }\) = 1,
∴ The maximum value of y is 1.
∴ Part (C) is the correct answer.
![]()