GSEB Solutions Class 12 Maths Chapter 7 Integrals Ex 7.6

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 7 Integrals Ex 7.6 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Integrals Ex 7.6

Integrate the following functions:
Question 1.
x sin x
Solution:
Let I = ∫x sin x dx
We know that ∫uv dx = u∫v dx – ∫(u’ ∫v dx)dx
Put u = x and v = sin x.
∴ I = x ∫sin x dx = ∫[(\(\frac{d}{dx}\) x) ∫sin x dx]dx
= – x cos x – ∫1. (- cos x)dx
= – x cos x + ∫cos x dx = – x cos x + sin x + C.

Question 2.
x sin 3x
Solution:
Let I = ∫xsin 3x dx. Taking u = x and v = sin 3x.

Question 3.
x²e^x
Solution:
Let I = ∫x²e^x dx, Put u = x² and v = e^xdx.

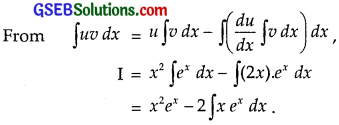
Taking x as I function, integrating again, we get

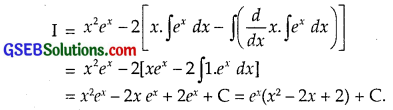
Question 4.
x log x
Solution:
Let I = ∫xlog x dx, Put u = log x and v = x.

Question 5.
x log 2x
Solution:
Let I = ∫xlog 2x dx = ∫(log 2x).x dx

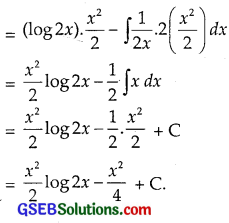
Question 6.
x²log x
Solution:

Question 7.
x sin^-1x
Solution:

Put x = sinθ so that dx = cosθdθ.

Question 8.
x tan^-1x
Solution:
Let I = ∫x tan^-1 x dx. Put x = tan^-1x and v = x.

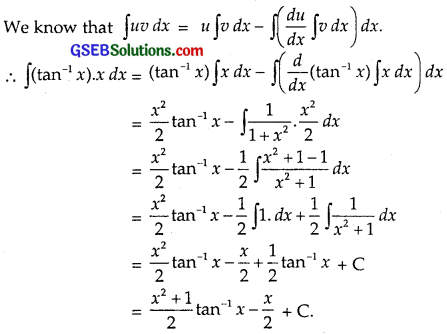
Question 9.
x cos^-1x
Solution:
Let I = ∫xcos^-1 x dx = ∫cos^-1 x.x dx

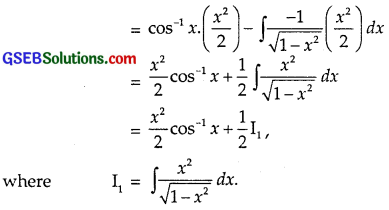
Putting x = cosθ so that dx = – sinθ dθ.

Question 10.
(sin^-1x)²
Solution:
Let I = ∫(sin^-1 x²)dx.
Put sin^-1x = θ ⇒ x = sin θ ⇒ dx = cosθ dθ.

Question 11.
\(\frac{x \cos ^{-1} x}{\sqrt{1-x^{2}}}\)
Solution:

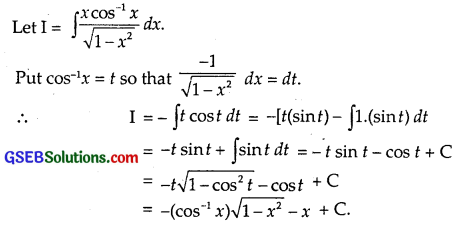
Question 12.
x sec²x
Solution:

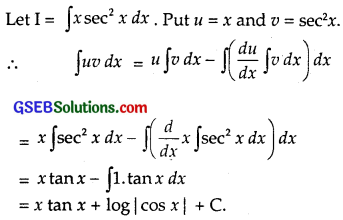
Question 13.
tan^-1x
Solution:

Question 14.
x(log x)²
Solution:

Question 15.
(x² + 1) log x
Solution:

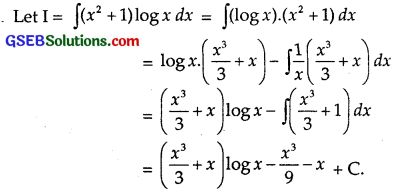
Question 16.
e^x(sin x + cos x)
Solution:
Let I = ∫e^x(sin x + cos x) dx.
Put e^xsin x = t so that (e^x.cos x + sin x.e^x)dx = dt.
⇒ e^x(sin x + cos x) dx = dt
∴ I = ∫dt = t + C = e^xsinx + C.

Question 17.
\(\frac{x e^{x}}{(1+x)^{2}}\)
Solution:

Question 18.
e^x(\(\frac{1+sinx}{1+cosx}\))
Solution:

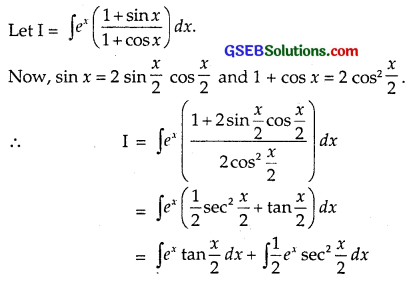
Taking tan \(\frac{x}{2}\) as I function and e^x as II function,
integrating ∫e^x tan \(\frac{x}{2}\) dx by parts, we get

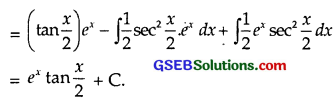
Question 19.
e^x(\(\frac{1}{x}\) – \(\frac{1}{x^{2}}\))
Solution:

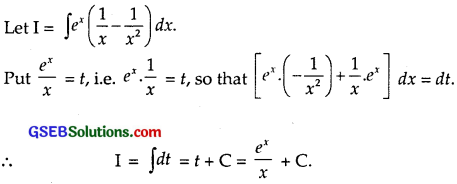
Question 20.
\(\frac{(x-3) e^{x}}{(x-1)^{3}}\)
Solution:

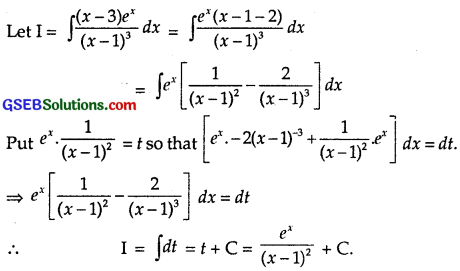
Question 21.
e^2xsinx
Solution:

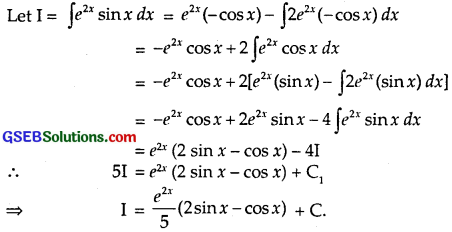
Question 22.
sin^-1(\(\frac{2 x}{1+x^{2}}\))
Solution:

Choose the correct answers in the following questions from 23 and 24:
Question 23.
∫ x² e^x3 dx equals
(A) \(\frac{1}{3}\) e^x3 + C
(B) \(\frac{1}{3}\) e^x2 + C
(C) \(\frac{1}{2}\) e^x3 + C
(D) \(\frac{1}{2}\) e^x2 + C
Solution:

∴ Part (A) is the correct answer.

Question 24.
∫ e^x secx(1 + tan x) dx equals
(A) e^x cosx + C
(B) e^x secx + C
(C) e^x sinx + C
(D) e^x tanx + C
Solution:

Taking sec x as I function and e^x as II function, integrating by parts
I₁ = (sec x) ∫e^x dx – ∫(sec x tan x ∫e^x dx)dx
= (sec x)e^x – ∫e^x sec x tan x dx
Putting this value in (1), we get
I = I₁ + ∫e^x sec x tan x dx
= (sec x)e^x – ∫e^x sec x tan x dx
Putting this value in (1), we get
I = I₁ + ∫e^x sec x tan x dx
= (sec x)e^x – ∫e^x sec x tan x dx + ∫e^x sec x tan x dx + C
= e^x sec x + C.
∴ Part (B) is the correct answer.