GSEB Solutions Class 12 Maths Chapter 7 Integrals Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 7 Integrals Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 7 Integrals Miscellaneous Exercise

Integrate the following functions w.r.t x (questions from 1 to 24):
Question 1.
\(\frac{1}{x-x^{3}}\)
Solution:
Let \(\frac{1}{x-x^{3}}\) = \(\frac{1}{x(1+x)(1-x)}\)
= \(\frac{A}{x}\) + \(\frac{B}{1+x}\) + \(\frac{C}{1-x}\)
⇒ 1 = A(1 + x)(1 – x) + Bx(1 – x) + Cx(1 + x) ………… (1)
Putting x = 0 in (1), we get
1 = A(1 + 0)(1 – 0) ⇒ A = 1.
Putting x = – 1 in (1), we get
1 = B(- 1)(1 + 1) ⇒ B = – \(\frac{1}{2}\)
Putting x = 1 in (1), we get
1 = C(1)(1 + 1) ⇒ C = \(\frac{1}{2}\).

Question 2.
\(\frac{1}{\sqrt{x+a}+\sqrt{x+b}}\)
Solution:

Question 3.
\(\frac{1}{x \sqrt{a x-x^{2}}}\)
Solution:

Question 4.
\(\frac{1}{x^{2}\left(x^{4}+1\right)^{\frac{3}{4}}}\)
Solution:

Question 5.
\(\frac{1}{x^{\frac{1}{2}}+x^{\frac{1}{3}}}\)
Solution:

Question 6.
\(\frac{5 x}{(x+1)\left(x^{2}+9\right)}\)
Solution:

Question 7.
\(\frac{sinx}{sin(x-a)}\)
Solution:

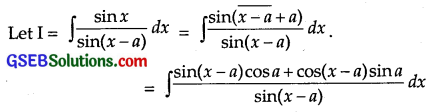
= cos a∫1 dx + sin a∫cot(x – a) dx
= (cos a)x + sin a log |sin(x – a)| + C
= x cos a + sin a log + |sin(x – a)| + C.

Question 8.
\(\frac{e^{5 \log x}-e^{4 \log x}}{e^{3 \log x}-e^{2 \log x}}\)
Solution:

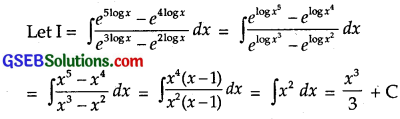
Question 9.
\(\frac{\cos x}{\sqrt{4-\sin ^{2} x}}\)
Solution:

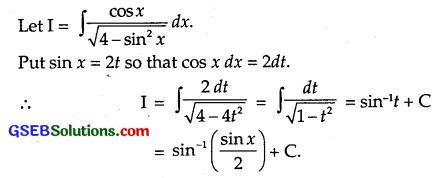
Question 10.
\(\frac{\sin ^{8} x-\cos ^{8} x}{1-2 \sin ^{2} x \cos ^{2} x}\)
Solution:

Question 11.
\(\frac{1}{cos(x+a)cos(x+b)}\)
Solution:

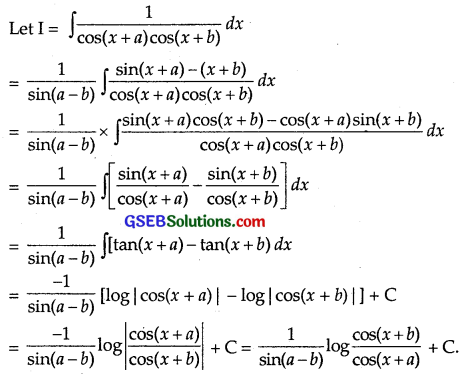
Question 12.
\(\frac{x^{3}}{\sqrt{1-x^{8}}}\)
Solution:

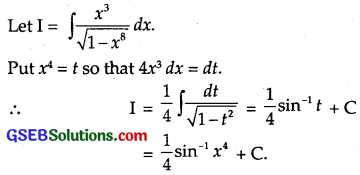
Question 13.
\(\frac{e^{x}}{\left(1+e^{x}\right)\left(2+e^{x}\right)}\)
Solution:

Question 14.
\(\frac{1}{\left(x^{2}+1\right)\left(x^{2}+4\right)}\)
Solution:

Question 15.
cos³xe^{log sinx}
Solution:

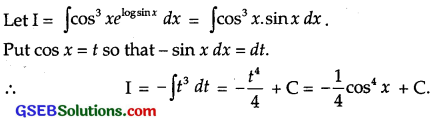
Question 16.
e^3logx(x⁴ + 1)^-1
Solution:

Question 17.
f'(ax + b)[f(ax + b)]ⁿ
Solution:

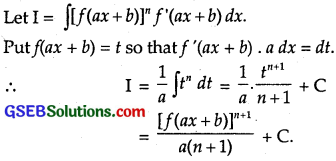
Question 18.
\(\frac{1}{\sqrt{\sin ^{3} x \sin (x+\alpha)}}\)
Solution:

Put cos α + cot x sin α = t so that – cosec²x sin α = dt.

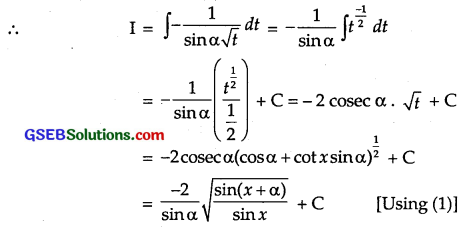
Question 19.
\(\frac{\sin ^{-1} \sqrt{x}-\cos ^{-1} \sqrt{x}}{\sin ^{-1} \sqrt{x}+\cos ^{-1} \sqrt{x}}\) x ∈ [0, 1]
Solution:

Question 20.
\(\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}\)
Solution:

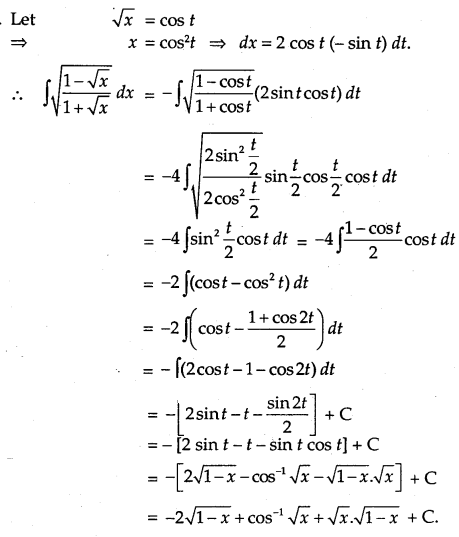
Question 21.
\(\frac{2+sin2x}{1+cos2x}\)e^x
Solution:

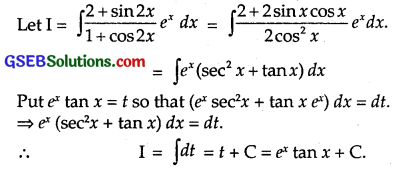
Question 22.
\(\frac{x^{2}+x+1}{(x+1)^{2}(x+2)}\)
Solution:

Question 23.
tan^-1\(\sqrt{\frac{1-x}{1+x}}\)
Solution:
Put x = cosθ so that dx = – sinθ dθ,

Question 24.
\(\frac{\sqrt{x^{2}+1}\left[\log \left(x^{2}+1\right)-2 \log x\right]}{x^{4}}\)
Solution:

Evaluate the following definite integrals from questions 25 to 33:
Question 25.
\(\int_{\frac{\pi}{2}}^{π}\) e^x(\(\frac{1-sinx}{1+cosx}\))dx
Solution:

Question 26.
\(\int_{0}^{\frac{\pi}{4}} \frac{\sin x \cos x}{\cos ^{4} x+\sin ^{4} x}\) dx
Solution:

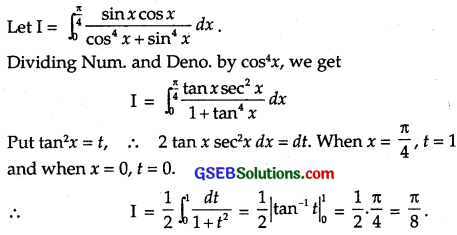
Question 27.
\(\int_{0}^{\frac{\pi}{2}} \frac{\cos ^{2} x}{\cos ^{2} x+4 \sin ^{2} x}\) dx
Solution:

Question 28.
\(\int\frac{3}{6} \frac{\sin x+\cos x}{\sqrt{\sin 2 x}}\) dx
Solution:

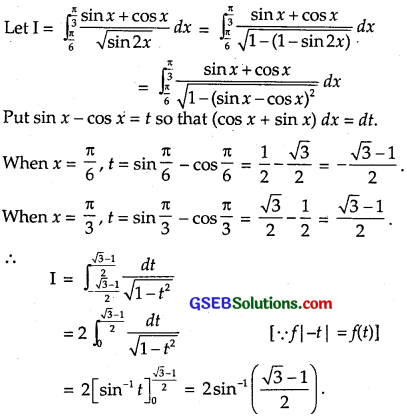
Question 29.
\(\int_{0}^{1} \frac{d x}{\sqrt{1+x}-\sqrt{x}}\)
Solution:

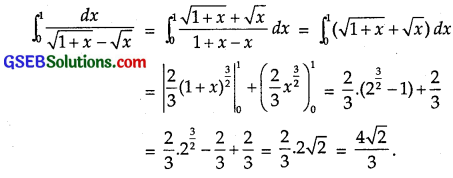
Question 30.
\(\int_{0}^{\frac{\pi}{4}} \frac{\sin x+\cos x}{9+16 \sin 2 x}\) dx
Solution:
Put sin x – cos x = t so that (cos x + sin x) dx = dt
and 1 – 2sin x cos x = t²  ⇒sin 2x = 1 – t^2.
When x = \(\frac{π}{4}\), t = sin \(\frac{π}{4}\) – cos \(\frac{π}{4}\) = \(\frac{1}{\sqrt{2}}\) – \(\frac{1}{\sqrt{2}}\) = 0.
When x = 0, t = sin 0 – cos 0 = – 1.

Question 31.
\(\int_{0}^{\frac{\pi}{2}}\)sin2xtan^-1x(sin x)dx
Solution:

Question 32.
\(\int_{0}^{\pi}\) \(\frac{xtanx}{secx+tanx}\) dx
Solution:

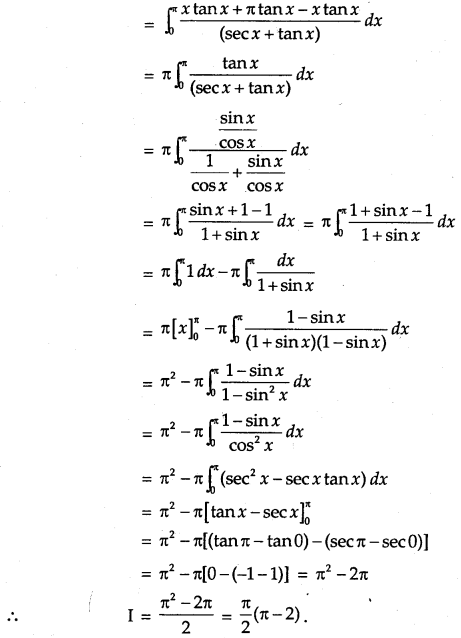
Question 33.
\(\int_{1}^{4}\)[|x – 1| + |x – 2| + |x – 3|] dx
Solution:

Prove the following questions 34 to 39:
Question 34.
\(\int_{1}^{3} \frac{d x}{x^{2}(x+1)}\) = \(\frac{2}{3}\) + log \(\frac{2}{3}\)
Solution:

Question 35.
\(\int_{0}^{1}\) xe^x dx = 1
Solution:
Let L.H.S. = I = \(\int_{0}^{1}\) xe^x dx.
Integrating by parts, taking x as a first function, we get

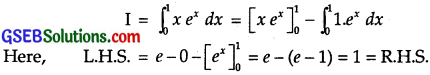
Question 36.
\(\int_{-1}^{-1}\) x¹⁷cos⁴x dx = 0
Solution:
I = \(\int_{-1}^{1}\) x¹⁷cos⁴x dx.
Let f(x) = x¹⁷cos⁴x, f(- x) = (- x)¹⁷cos⁴(- x)
= – x¹⁷cos⁴x
∴ I = 0 = R.H.S. [∵ \(\int_{-a}^{a}\) f(x) = 0 if f(- x) = – f(x)]

Question 37.
\(\int_{0}^{\frac{\pi}{2}}\)sin³x dx = \(\frac{2}{3}\)
Solution:

Question 38.
\(\int_{0}^{\frac{\pi}{2}}\)2tan³ x dx = 1 – log x
Solution:

Question 39.
\(\int_{0}^{1}\)sin^-1x dx = \(\frac{π}{2}\) – 1
Solution:

Question 40.
Evaluate \(\int_{0}^{1}\)e^2-3x dx as a limit of a sum.
Solution:
Here, a = 0, b = 1, f(x) = e^2-3x, h = \(\frac{1-0}{n}\) = \(\frac{1}{n}\) or nh = 1.

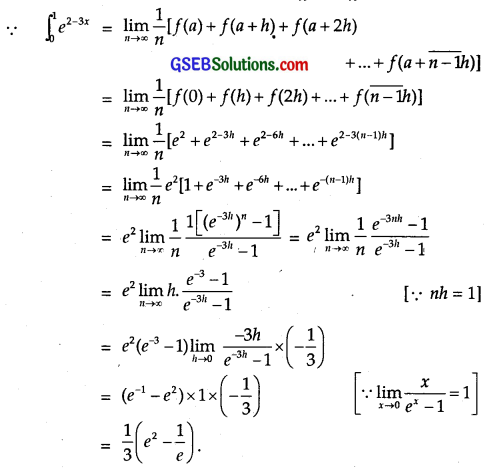
Choose the correct answers in the following questions 41 to 44:
Question 41.
∫\(\frac{d x}{e^{x}+e^{-x}}\) is equal to
(A) tan^-1(e^-x) + C
(B) tan^-1(e^-x) + C
(C) log(e^x – e^-x) + C
(D) log(e^x + e^-x) + C
Solution:

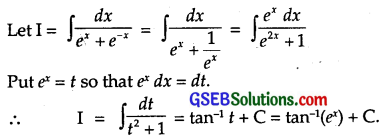
∴ Part (A) is the correct answer.

Question 42.
∫\(\frac{\cos 2 x}{(\sin x+\cos x)^{2}}\) dx is equal to
(A) \(\frac{-1}{sinx+cosx}\) + C
(B) log|sin x + cos x| + C
(C) log|sin x – cos x| + C
(D) \(\frac{1}{(\sin x+\cos x)^{2}}\)
Solution:

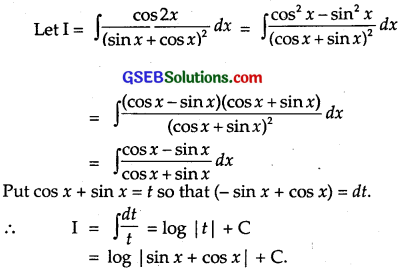
∴ Part (B) is the correct answer.

Question 43.
If f(a + b – x) = f(x), then \(\int_{a}^{b}\) x f(x) dx is equal to
(A) \(\frac{a+b}{2}\) \(\int_{a}^{b}\) f(b – x) dx
(B) \(\frac{a+b}{2}\) \(\int_{a}^{b}\) f(b + x) dx
(C) \(\frac{b-a}{2}\) \(\int_{a}^{b}\) f(x) dx
(D) \(\frac{a+b}{2}\) \(\int_{a}^{b}\) f(x) dx
Solution:

∴ Part (D) is the correct answer.

Question 44.
The value of \(\int_{0}^{1}\) tan^-1(\(\frac{2 x-1}{1+x-x^{2}}\)) dx is
(A) 1
(B) 0
(C) – 1
(D) \(\frac{π}{4}\)
Solution:

Adding (1) and (2), we get
2I = 0 or I = 0.
∴ Part (B) is the correct answer.