Gujarat Board GSEB Textbook Solutions Class 12 Physics Chapter 11 Dual Nature of Radiation and Matter Textbook Questions and Answers, Additional Important Questions, Notes Pdf.
Gujarat Board Textbook Solutions Class 12 Physics Chapter 11 Dual Nature of Radiation and Matter
GSEB Class 12 Physics Dual Nature of Radiation and Matter Text Book Questions and Answers
Question 1.
Find the
(a) maximum frequency, and
(b) the minimum wavelength of X- rays produced by 30 kV electrons.
Solution:
V = 30 kV = 30 x 103V,
Kmax = eV = 1.6 x 10-19 x 30 x 103
(a) hυ = eV
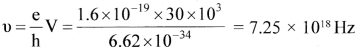
b. v = υλ
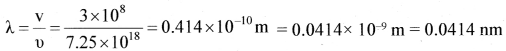
Question 2.
The work function of cesium metal is 2.14 eV. When the light of frequency 6 x 1014 Hz is incident on the metal surface, photoemission of electrons occurs. What is the
(a) the maximum kinetic energy of the emitted electrons
(b) stopping potential, and
(c) maximum speed of the emitted photo electrons?
Solution:
ø0 = 2.14 eV = 2.14 x 1.6 x 10-19 J, υ = 6 x 1014 Hz
(a) \(\frac {1}{2} \)mvmax = hυ – ø0 = 6.62 x 1034 x 6 x 1014 Hz – 2.14 x 1.6 x 10-19
= 39.72 x 1020 – 34.24 x 10-20 = 5.48 x 10-20= 0.548 x 10-19 J

Question 3.
The photoelectric cut-off voltage in a certain experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons emitted?
Solution:
V0 = 1.5 V
Kmax =\(\frac {1}{2} \)mV2max = eV01.6 x 10-19 x 1.5 = 2.4 x 10-19J
![]()
Question 4.
Monochromatic light of wavelength 632.5 nm is produced by a helium-neon laser. The power emitted is 9.42 m W.
(a) Find the energy and momentum of each photon in the light beam.
(b) How many photons per second, on the average, arrive at a target irradiated by this beam? (Assume the beam to have uniform cross-section which is less than the target area).
(c) How fast does a hydrogen atom have to travel in order to have the same momentum as that of the photon?
Solution:
λ = 632.8 nm = 632.8 x 10-9m, P = 9.42 m W = 9.42 x 10-3 W

Question 5.
The energy flux of sunlight reaching the surface of the earth is 1.388 X 10 W/m2. How many photons (nearly) per square metre are incident on the earth per second? Assume that the photons in the sunlight have an average wavelength of 550 nm.
Solution:
E = 1.388 x 10-3Wm-2
λ = 550 nm = 550 x 10-9m
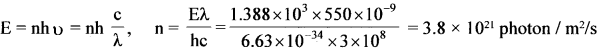
Question 6.
In an experiment on the photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be 4.12 x 10-15 V s. Calculate the value of Planck’s constant.
Solution:
Slope of the cut off voltage versus frequency of incident light graph = 4.12 x 10-15 Vs
but the slope of the graph = \(\frac { h }{ e } \)
h = e x slope of the graph
= 1.6 x 1019 x 4.12 x 10-15
= 6.592 x10-34Js
Question 7.
A 100 W sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is Incident on It. The wavelength of the sodium light is 589 nm.
(a) What is the energy per photon associated with sodium light?
(b) At what rate are the photons delivered to the sphere?
Solution:
P = 100 W λ = – 589 nm = 589 x 10-9m
(a) E = hυ = h \(\frac {c}{λ} \) = ![]() = 0.03 x 10-17 = 3 x 10-19
= 0.03 x 10-17 = 3 x 10-19
(b) Let ‘n’ be the number of photons produced/s
then. hυ = P ∴n = \(\frac {p}{λυ} \) = \(\frac{100}{3 \times 10^{-14}}\) = 3.3 x 1020
Question 8.
The threshold frequency for a certain metal is 3.3 X 1014 Hz. if light of frequency 8.2 x 1014 Hz is Incident on the metal, predict the cut-off voltage for the photoelectric emission.
Solution:
υ0 = 3.3 1014Hz, υ = 8.2 x 1014Hz
mv2max = h(υ – υ0),
But eV0 = \(\frac {1}{2} \) mv2max
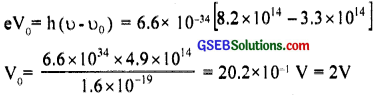
Question 9.
The work function for a certain metal Is 4.2 eV. Will this metal give photoelectric emission for incident radiation of wavelength 330 nm?
Solution:
ø0 = 4.2 eV
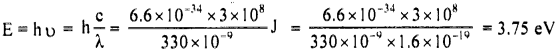
ø0>E, so not possible.
![]()
Question 10.
Light of frequency 7.21 x 10 Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 x 10 m/s are ejected from the surface. What is the threshold frequency for the photoemission of electrons?
Solution:
u = 7.21 x 1014 Hz, v = 6 x 105ms-1
\(\frac {1}{2} \) mv2max = h(υ – υ0) = hυ – hυ0
hυ0 = hυ – \(\frac {1}{2} \) mv2max
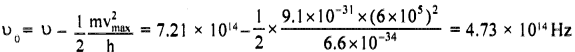
Question 11.
Light of wavelength 488 nm is produced by an argon laser which Is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut – off) potential of photoelectrons is 0.38 V. Find the work function of the material from which the emitter b made.
Solution:
λ = 488 nm = 488 x 10-9m, υ0 = 0.38 V
hu = ø0 + \(\frac {1}{2} \) mv2max, h = \(\frac {c}{λ} \) Ø0 + eV0
![]()
Question 12.
Calculate the
(a) momentum, and
(b) de Broglie wavelength of the electrons accelerated through a potential difference of 56 V
Solution:
(a) v = 56 V
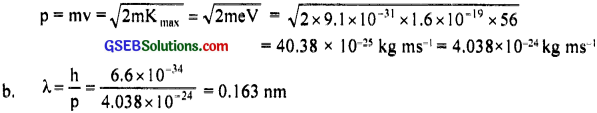
Question 13.
What Is the
(a) momentum, (b) speed, and
(c) de Brogue wavelength of an electron with the kinetic energy of 120 eV.
Solution:
Solution:
Kmax = 120 eV

Question 14.
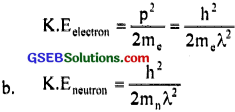
The wavelength of light from the spectral emission line of sodium Is 589 nm. Find the kinetic energy at which
(a) an electron, and
(b) a neutron would have the same dc Brogue wavelength.
Solution:
(a) de Broglie wavelength, λ = \(\frac {h}{p} \)
Question 15.
What Is the de Broglie wavelength of
(a) a bullet of mass 0.040 kg traveling at the speed of 1.0 km/s,
(b) a ball of mass 0.060 kg moving at a speed of 1.0 m/s, and
(c) a dust particle of mass 1.0 X 10-9 kg drifting with a speed of 2.2 m/s?
Solution:
m = 0.04 kg, v = 1 x 103ms-1

Question 16.
An electron and a photon each have a wavelength of 1.00 nm. Find
(a) their momenta,
(b) the energy of the photon, and
(c) the kinetic energy of electrons.
Solution:
λ = 1 x 10-9 m

Question 17.
(a) For what kinetic energy of a neutron will the associated de Broglie wavelength be 1.40 x 10-10 m?
(b) Also find the de Broglie wavelength of a neutron, in thermal equilibrium with matter, having an average kinetic energy of (3/2) kT at 300 K.
Solution:
λ = 1.40 x 10-10m

Question 18.
What is the de Broglie wavelength of a nitrogen molecule in air at 300 K? Assume that the molecule is moving with the root-mean-square speed of molecules at this temperature. (Atomic mass of nitrogen = 14.0076 u)
Solution:
T = 300 K λ = ?
m = 14.0076 u = .14.0076 x 1.6 x 10-27kg
K max = K T = \(\frac {3}{2} \) x 1.38 x 10-23 x 300 = 6.21 x 10-21J

GSEB Class 12 Physics Dual Nature of Radiation and Matter Additional Important Questions and Answers
Question 1.
What are the different methods to release electrons?
Answer:
1. Thermionic emission, Photoelectric emission, Field emission, Secondary emission
Question 2.
What happens when a negative potential is applied to the anode?
Answer:
Kinetic energy of the photoelectrons decreases
Question 3.
What happens when this negative potential is increased?
Answer:
Photoelectric current decreases.
Question 4.
What happens if the intensity of light is increased, when the frequency is less than the threshold value?
Answer:
Photoelectric emission is not possible.
![]()
Question 5.
What happens w the energy of (lie photon incidents on metal surfizee?
Answer:
One part of the energy of the photon is used in ejecting out the electrons from the metal surface and the remaining part of the energy of the photon is used to impart K.E to the emitted electrons.
Question 6.
If radio,, possesses dual nature, what is the nature of neater? Justify.
Answer:
Dual Nature. Because nature loves symmetry
Question 7.
how can you increase the KE and intensity of the electron beam?
Answer:
By increasing accelerating potential, we can increase KE and by increasing the filament current we can increase the intensity of the electron beam.
Question 8.
The figure below represents the variation of current with potential for a metal.
Answer:
(a) Identify the situation.
(c) Even when the potential is zero, there is current. Explain.
(d) Current is zero for a particular potential. How does this potential help indeter mining the velocity of electrons?
Answer:
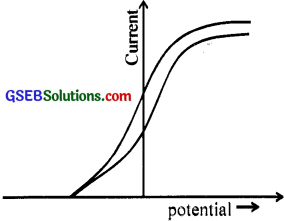
(a) Photoelectric effect
(c) incident photon possesses suitable energy in even though the potential is zero.
(d) Using the relation eV0 = \(\frac {1}{2} \) mv2
V = \(\sqrt{\frac{2 \mathrm{eV}_{0}}{\mathrm{~m}}}\) V0 – stopping potential
Question 9.
The size of the bacteria can be magnified 60,0000 times using an electron microscope. The wave nature of electrons is used in electron microscopes.
(a) Name the type of waves used here
(c) Why is this wave character no, observed in large bodies?
Answer:
(a) dc-Broglie waves
(c) For large bodies m is very large and hence is very small.
![]()
Question 10.
(a) Name the experiment which establishes the wave nature of moving electrons.
(b) In that experiment. electrons are accelerated through cl potential of 54 V and ¡s made to fall normally on the nickel crystal of interatomic separation 0. 91 A. Draw the polar graph showing the variation of intensity of the scattered electrons and latitude angle at this potential.
(c) Explain the variation of intensity with latitude angle from the polar graph.
(d) Calculate the dc-Brogue wavelength of the electron.
Answer:
(a) Davisson-Germer experiment.
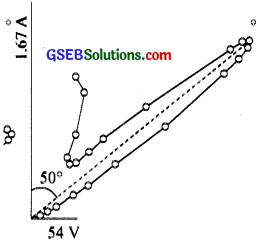
(c) Intensity decreases with latitude angle and then increases to maximum at 500
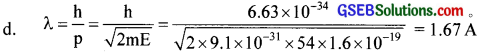
Question 11.
Pick the odd one out.
(a) Interference
(b) Diffraction
(c) Polarisation
(d) Photoelectric effect
Answer:
d
Question 12.
Classify the following properties of the waves into de Broglie wave, e.m wave and sound wave.
i. Associated with the moving particle
ii. Longitudinal wave
iii. Electric field and magnetic field are perpendicular to each other
iv. can produce the photoelectric effect
v. Wavelength Ls inversely proportional to the mass of the moving particle
vi. Velocity in vacuum is 3 x 108 m/s
Answer:
de Broglie wave – i, v
e.m wave – iii, iv, vi
Sound wave – ii
![]()
Question 13.
Pick the odd one out
Figure shows results of an experiment involving photoelectric effect.
(a) Beam B has the highest frequency
(b) Beam C has the largest wavelength
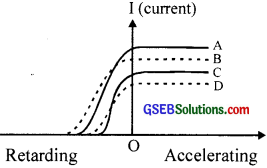
(c) Beam A has the highest rate of photoelectric emission
(d) Beam D has the least frequency
(e) Photo electrons ejected &v beam B have the highest moment.
Answer:
d
Question 14.
Fill in the blanks.
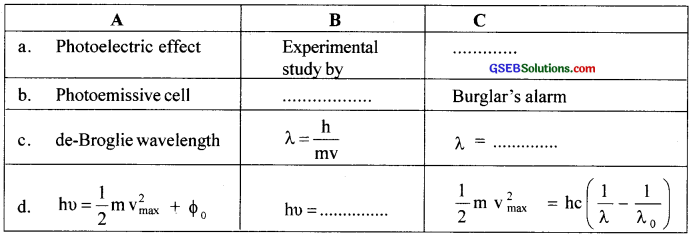
Answer:
(a) Philip Lenard
(b) Light energy is converted into electrical energy
(c) λ = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{meV}}}\)
(d) hυ = \(\frac{1}{2}\) mv2max + hυo
Question 15.
Maid, the following
| A | B |
| a. Intensity’ of radiation | i. electron volt |
| b. Photo voltage cell | ii. shorter the dc-Brogue wavelength |
| c. Larger mass | iii. is directly proportional to currents. Work function |
| d. Work function | iv. no battery is required |
| v. is inversely proportional to current | |
| vi. larger the de-Broglie wavelength |
Answer:
(a) is directly proportional to current
(b) no battery is required
(c) shorter the dc-Brogue wavelength
(d) electron volt
Answer:
(a) Intensity of photocurrent is directly proportional to the intensity of incident light.
(b) Photoelectric current intensity is independent of frequency.
![]()
Question 16.
It has been determined experimentally that when light falls on a metal surface, the surface emits electrons. For example. you can start a current in a circuit just by shining a light on a metal plate.
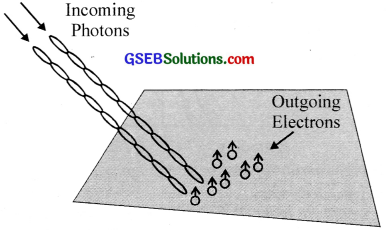
(a) What is your explanation?
(b) Mention some other methods in which electron emission is possible.
(c) Are stopping potential and cut off potential the same?
Answer:
(a) The electrons in the metal surface absorb photon energy and are emitted.
(b) Thermionic emission, photoelectric effect. field emission, secondary emission.
(c) Yes
Question 17.
(a) Dra’s’ the graph showing ¡he variation of potential with the frequency of incident radiation.
(b) What does the slope of ¡he graph represent?
(c) From the slope how will you find the value of ‘h’?
Answer:
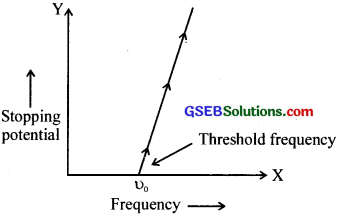
(b) Slope of the graph gives \(\frac{h}{e}\)
(c) Knowing the slope from the graph and the value of’e’, we can find the value of h.
Question 18.
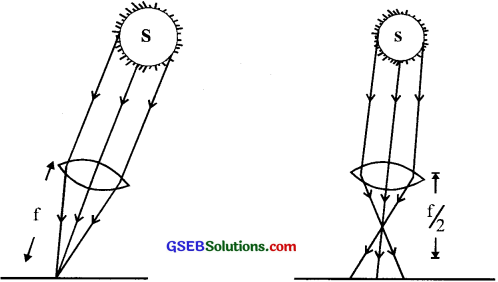
An image of the sun is formed on the metal surface of the photoelectric cell and it produces a current. The lens forming the image is then replaced by another of the same diameter but only half in focal length.
(a) What will he the effect on the photo electric current?
(b) Is photoelectric emission possible at all frequencies?
(c) If not give your explanation.
Answer:
(a) No change
(b) No. Only at or above the threshold frequency
(c) The energy of the incident photon should be at least equal to or greater than the work function of the metal.
![]()
Question 19.
All the photoelectrons are not emitted with the same energy Give reason.
Answer:
The energy of the incident photons is spent for providing work function and KE. The work function is the same for all electrons then changes depending on its energy state.
Question 20.
Light is incident Of the cathode of a photocell and the slopping voltages are measured for the light of two different wavelengths, are given below.

(a) Determine the wave function of the metal of the cathode in e V
(b) Find the value of the universal constant
(c) Define stopping potential and work function.
(d) Can you suggest a mathematical relation between kinetic energy and stopping potential?
Answer:
(a) \(\frac{hc}{λ} \) = eV0
Answer:
2.3 eV
(b) 1.24 x 10-6
(c) If the applied potential is negative, the photoelectric current decreases and becomes zero for a certain negative value. This value
of potential is called stopping potential or cut-off potential. The minimum amount of work required to emit electrons from a metal surface is called work function.
(d) eV0 = Kmax
Question 21.
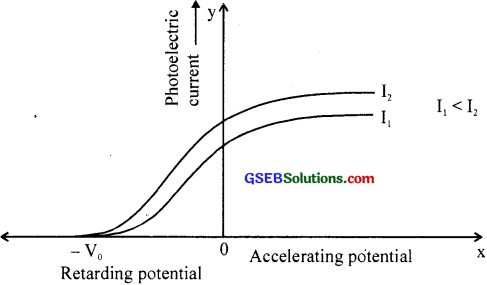
The graph shows the variation of photoelectric current with accelerating potential of different Intensities.
(a) What conclusion do you arrive at from the graph?
(b) Photoelectric current is not zero even f the accelerating voltage is zero. Justify your answer.
(c) Why two curves meet at one point on the retarding potential axis?
Answer:
(a) As intensity increases, the intensity of photocurrent also increases.
(b) Because all electrons are not ejected with the same KE. When acceleration voltage is zero, these electrons are ejected with same velocity and can reach the collecting electrode,
(c) The frequency of incident light is the same for I and I,
![]()
Question 22.
The data of a photoelectric effect experiment are given below.

(a) Draw υ – Ek graph.
(b) From the graph find work function and Planck c constant.
(c) Can you suggest a relation among incident energy of photon, work function and maximum kinetic energy?
Answer:
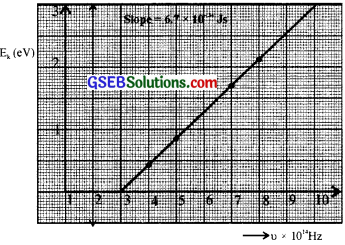
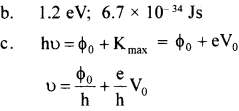
Question 23.
The above graph shows frequency of an incident photon and maximum kinetic energy of a photoelectric effect
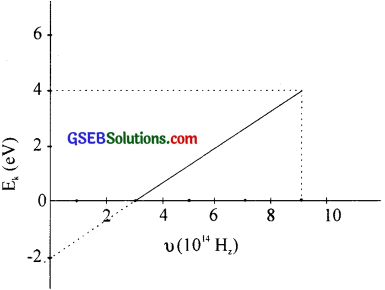
(a) What is the value of threshold frequency and threshold wave length?
(b) What is the work function of the cathode in e V?
(c) Find the maximum kinetic energy if the frequency of photon is 9 x 1014 Hz.
(d) Also find the value of Planck ‘s constant (h).
Answer:
(a) 3 x 1014Hz; 10-6m
(b) 2 eV
(c) KE = hυ – 40 = 3.85 eV = 4eV (0.4 eV from graph)
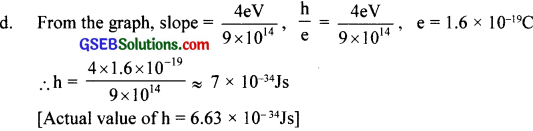
Question 24.
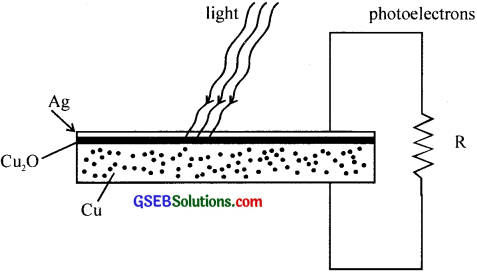
(a) What is the purpose of Cu2 O?
(b) Which plaie becomes positive?
(c) Which plate becomes negative?
Answer:
(a) Cuprous oxide is a photosensitive semiconductor.
(b) Cu
(c) Ag
Question 25.
(a) Why de-Broglie wave associated with a moving car is not visible?
(b) What is de-Broglie hypothesis?
(c) Give expressions for de-Broglie wavelength.
Answer:
(a) Mass is too large
(b) Every material particle in the state of motion possesses an associated wave where wavelength is given by λ = \(\frac{h}{p} \) where h is the Plank’s constant and p- the momentum.
(c) λ = \(\frac{h}{p} \)
![]()
Question 26.
(a) Give the expression showing the relation between energy and momentum of a photon.
(b) “de-Broglie wavelength supports Bohr ‘s model of stationary orbits.” Comment on this statement.
(c) is there any difference between the wavelength of the radiation and dc-Brogue wave length of a photon of that radiation? Explain.
Answer:
(a) Momentum of photon = \(\frac{hυ}{c} \)
(b) Bohr orbit condition, mvr = \(\frac{nh}{2π} \)
i.e., pr = \(\frac{nh}{2π} \)
taking \(\frac{h}{p} \) = \(\frac{2πr}{n} \) = \(\frac{L}{n} \)This suggests that λ = \(\frac{L}{n} \) or total length of the orbit is n times de Broglies wavelength.
(c) No. Wavelength of radiation λ = \(\frac{c}{υ} \)
de Broglie’s wavelength λ = \(\frac{h}{p} \) = \(\frac{c}{υ} \)
Question 27.
(a) The wave nature of matter is not noticeable in our daily observations. Justify your
Answer.
(a) For a very small dust particle of radius 10-6 (1µm); density p = 104 kg/m3 moving with a velocity of 0.01 m/s, its momentum p is –
p = mv = \(\frac {4}{3} \) πr3 pv = \(\frac {4}{3} \)π x (10-6)3 x 104 x 0.01
p ≈ 4 x 10-16 kg m/s
de Broglie wavelength associated with this particle is –
![]()
This value of A is extremely small compared to the dimension of any physical system.
Question 28.
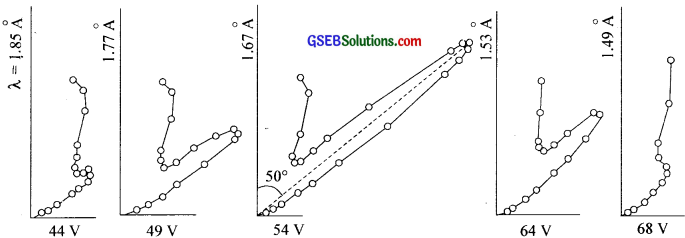
What do the graphs represent?
Answer:
Intensity of scattered electrons versus incident angle.
Question 29.
Which of the following statements are is not correct about a photon?
(a) Photon exerts no pressure.
(b) Momentum of photon is \(\frac {hυ}{c} \)
(c) Rest mass of a photon is zero.
(d) Energy of a photon is ho.
Answer:
a and c
Question 30.
(a) Every metal has a definite work function. Why all photo electrons do not come out with the same energy of incident radiation in monochromatic? Why there is an energy distribution of photo electrons?
(b) The energy and momentum of an electron are related to the frequency and wave length of the associated matter wave by the relations.
E = hυ, p = \(\frac {h}{λ} \)
But while the value of λ is physically significance the value of υ (and therefore the value of the phase speed υλ) has no physical significance. Why?
Answer:
(a) Work function is the minimum amount of energy required for the electron in the topmost level of the conduction band to get out of the metal. All the electrons do not belong to this topmost level. Different electrons are knocked off from the metal from different levels, with different energy for the same incident radiation. Thus the emitted electrons occupy a continuous band of energy levels.
(b) The absolute value of energy E (but not momentum, p) of any particle is arbitrary to within an additive constant. Hence absolute value of ‘υ’of a matter wave has no direct physical meaning, while ‘λ‘ is physically significant. The phase speed (υλ) is physically insignificant. while group speed is physically significant.
![]()
Question 31.
Even though metals have free electrons, they cannot escape from metal surface. Why?
Answer:
If an electron tends to escape from metal surface, the atom which is losing the electron becomes a positive ion and pulls back the electron to itself. Hence free electrons of metals cannot escape from the surface.
Question 32.
Define 1 eV
Answer:
1 eV is the energy gained by an electron when it is accelerated by a potential difference of
lV.l eV= 1.609 x 10-19 J.
Question 33.
What are the factors on which the rate of thermionic emission depends?
Answer:
The rate of thermionic emission depends on the temperature and work function of the metal. Higher the temperature, greater will be thermionic emission. For metals with lower work function, thermionic emission occurs at low temperatures.
Question 34.
Does the photoelectric effect violate the law of conservation of energy?
Answer:
No, the photoelectric effect does not violate the law of conservation of energy. In the photoelectric effect, light is converted to electrical energy.
Question 35.
Give example’s for metals sensitive to UV rays and then for visible light.
Answer:
Zinc, cadmium and magnesium are sensitive to UV light. Lithium, sodium, potassium, cesium, and rubidium are sensitive to visible light.
Question 36.
Why is photocurrent proportional to intensity?
Answer:
The number of photoelectrons emitted per second is proportional to the intensity of incident radiation. Hence photocurrent increases with the intensity of light.
![]()
Question 37.
What is saturation current?
Answer:
The maximum value of photoelectric current obtained by increasing the accelerating positive potential is called saturation current. The Saturation current is proportional to the intensity of incident radiation.
Question 38.
How does a fire alarm work?
Answer:
In fire alarm, a number of photocells are installed at suitable places in a building. In the event of breaking out of fire. light radiation and IR light fall upon photocell, making an electric bell or siren to ring.
Question 39.
Does wave theory give a proper explanation for the photoelectric effect?
Answer:
No. On the basis of wave theory, the photoelectric effect cannot be instantaneous, and also it should occur even for the light of frequency less than the threshold frequency.
Question 40.
Why is light 1101 deflected by an electric and magnetic fields?
Answer:
Light being an electromagnetic wave, does not consist of charged particles. Hence light is not deflected by electric or magnetic fields.
Question 41.
Why are alkali metal most suited for photoelectric emission?
Answer:
The work function of alkali metal is quite low and also its threshold energy ¡s almost equal to that of photons of visible light. For this reason alkali metals are most suited for photoelectric emission.
Question 42.
Why wooden surface does not exhibit a photoelectric effect?
Answer:
The wooden surface does not have free electrons. The work function of wood ¡s much larger
when compared to metals. Hence wooden surface does not exhibit a photoelectric effect.
Question 43.
A fast-moving bullet is not diffracted by a crystal surface, while an electron diffracts. Why?
Answer:
The wavelength of bullet is of the order of 10-31 m while that of an electron is 10-10 m. Diffraction is possible when the width of the aperture is of the order of the same order as that of wave. Inter atomic distance of the crystal is 10 ‚° m. Hence only electrons get diffracted.
Question 44.
An electron and a proton have same speed. How are their wavelength related?
We know de Broglie λ =\(\frac {h}{mv} \) i.e., λ ∝\(\frac {1}{m} \) As proton is heavier than electron. wavelength of proton is less than that of electron.
Question 45.
Millikan verified Einstein c photoelectric equation. How?
Answer:
According to Einstein’s photoelectric equation. \(\frac {1}{2} \) mv2max = h(υ – υ0)
if V0 is the stopping potential, then
\(\frac {1}{2} \) mv2max = eV0
Combining the above two equations we get
eV0 = hυ – hυ0 or V0 = \(\frac {h}{e} \)υ – \(\frac {h}{e} \)υ0
The above equation predicts that the V0 versus u curve is a straight line with slope \(\frac {h}{e} \)
R.A. Millikan experimentally studied the nature of stopping potential versus frequency curve for different metals. From his experiments he got straight line as predicted by Einstein’s equation. Not only that he also calculated the value of h using known value of’e’ and the slope obtained.
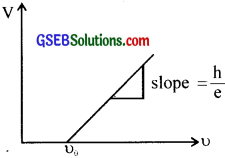
The result obtained (6.626 x 10-34 Js) was in agreement with the actual value of ‘h’. Thus Millikan experimentally verified Einstein’s photoelectric equation.
![]()
Question 46.
can a proton and an electron have the same de Brogue wavelength?
Answer:
Yes. A proton and an electron can have equal de Broglie wavelength if they have same momentum.