GSEB Solutions Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

Gujarat Board GSEB Textbook Solutions Class 12 Physics Chapter 9 Ray Optics and Optical Instruments Textbook Questions and Answers, Additional Important Questions, Notes Pdf.

Gujarat Board Textbook Solutions Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

GSEB Class 12 Physics Ray Optics and Optical Instruments Text Book Questions and Answers

Question 1.
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. if the candle is moved closer to the mirror, how would the screen have to be moved?
Answer:
u = -27 cm, f = -18 cm
\(\frac {1}{v} \) + \(\frac {1}{u} \) = \(\frac {1}{f} \),
\(\frac {1}{-27} \) + \(\frac {1}{v} \) = \(\frac {1}{-18} \)
∴ v = \(\frac{-18 \times 27}{27-18}\) = – 54 cm
m = \(\frac{\mathrm{h}_{\mathrm{i}}}{\mathrm{h}_{\mathrm{o}}}\) = \(\frac {-v}{u} \),
\(\frac{\mathrm{h}_{\mathrm{i}}}{2.5}\) = \(\frac{-(-54)}{(-27)}\) = -2
h_i = -5 cm
∴ The image is real, inverted and magnified.

Question 2.
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
Answer:
u = -12 cm, f = 15 cm. h₀ = 4.5 cm
\(\frac {1}{v} \) + \(\frac {1}{u} \) = \(\frac {1}{f} \), \(\frac {1}{v} \) + \(\frac {1}{(-12)} \) = \(\frac {1}{15} \)
v = \(\frac{15 \times 12}{15+12}\) = \(\frac{15 \times 12}{27}\) = \(\frac{20}{3}\) = 6.67 cm
Image is 6.67 cm behind the mirror.

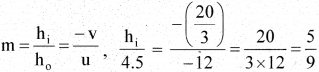
h_i = \(\frac {5 x 4.9}{9} \) = 2.5 cm
Image is virtual, erect and diminished

Question 3.
A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? if water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again?
Answer:

i.e., depth in liquid = 7.66 cm
Distance through which microscope has to he moved 9.4 – 7.66 1 .74 cm

Question 4.
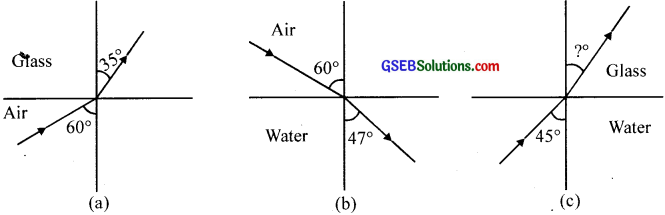
Figures (a) and (b) show the refraction of a ray in air incident at 600 with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in a glass when the angle of incidence in water is 450 with the normal to a water-glass interface (fig. c).

Answer:

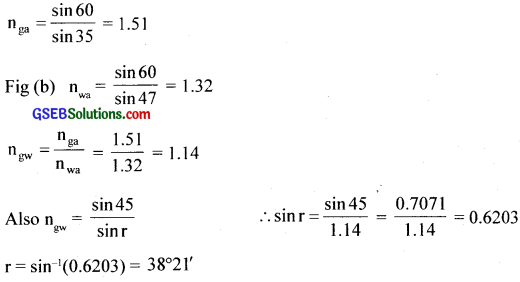
Question 5.
A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? The Refractive index of water is 1.33. (Consider the bulb to be a point source.)
Answer:

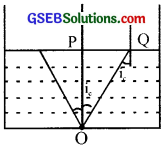
n = 1.33
∴ n = \(\frac{1}{\sin \mathrm{i}_{\mathrm{c}}}\)
∴ sin i_c = \(\frac{1}{1.33}\)
∴ i_c = 48°45’
OP = 80 cm
From the figure, tan i_c = \(\frac{PQ}{OP}\)
PQ = OP tan i_c = 80 × tan 48°45’ = 91.22 cm
∴ Area of the surface of water = t (PQ)² = 3.14(91.22)² 2.61 m²

Question 6.
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be 400. What is the refractive index of the material of the prism? The refracting angle of the prism is 600. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
Answer:

Question 7.
Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be 20 cm?
Answer:
\(\frac{1}{f}\) = (n – 1) [ \(\frac{1}{R_{1}}-\frac{1}{R_{2}}\) ]
f = 20 cm. n = 1.55. R₁ = R, R₂ = – R
∴ \(\frac{1}{20}\) = (1.55 – 1) [ \(\frac{1}{R}+\frac{1}{R}\) ] = 0.55 x \(\frac{2}{R}\)
R = 0.55 x 2 x 20 = 22 cm

Question 8.
A beam of light converges at a point P. Now a lens ¡s placed in the path of the convergent beam 12 cm from P. At what point does the beam converge if the lens is (a) a convex lens of focal length 20 cm, and (b) a concave lens of focal length 16 cm?
Answer:
(a) \(\frac{1}{v}\) – \(\frac{1}{u}\)= \(\frac{1}{f}\) f = 20 cm. u = + 12 cm (object on the right)
\(\frac{1}{v}\) = \(\frac{1}{20}\) + \(\frac{1}{+12}\) = \(\frac{20 + 12}{20 x 12}\)
\(\frac{32}{240}\) = \(\frac{2}{15}\)
∴v = 7.5 cm
A real image is formed 7.5 cm away from the lens.

(b) \(\frac{1}{v}\) = \(\frac{1}{f}\) + \(\frac{1}{u}\) = \(\frac{1}{-16}\) + \(\frac{1}{12}\) = \(\frac{-12 + 16}{16 x 12}\) = \(\frac{4}{16 x 12}\) = \(\frac{1}{48}\)
∴v = 48 cm
A real image is formed at 48 cm away from the lens

Question 9.
An object of size 3.0 cm is placed 14 cm in front of a concave lens of focal length 21 cm. Describe the image produced by the lens. What happens if the object is moved further away from the lens?
Answer:
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)
f = -21 cm,
u = -14 cm,
h = 3 cm
\(\frac{1}{v}\) = \(\frac{1}{f}\) + \(\frac{1}{u}\) = \(\frac{1}{-21}\) + \(\frac{1}{-14}\)
∴v = \(\frac{-42}{5}\) = – 8.4 cm

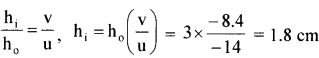
Image is virtual, erect and diminished, formed on the same side of the object If the object is moved away from the lens, image moves towards the focus and decreases in size.

Question 10.
What is the focal length of a convex lens of focal length 30 cm ¡n contact with a concave lens of focal length 20 cm? Is the system a converging or a diverging lens? Ignore the thickness of the lenses.
Answer:
f₁ = 30 cm, f₂ = – 20 cm

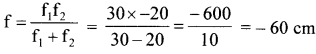
‘f’ is negative, the combination is a diverging lens.

Question 11.
A compound microscope consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective should an object be placed in order to obtain the final image at (a) the least distance of distinct vision (25 cm), and (b) at infinity? What is the magnifying power of the microscope in each case?
Answer:
f₀ = 2 cm. f_e = 6.25 cm
Distance between object lens and eyepiece = 15 cm
(a) For the formation of image at the least distance of distinct vision, v_e = – 25 cm

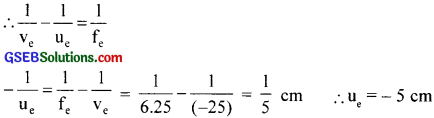
Object is on the left of the object lens.
Distance of the image from the objective lens = 15 – 5 = 10 cm
i.e.,v₀ = 10 cm

(b) When final image is at infinity, then object must be placed at the focus of the eyepiece.

Question 12.
A person with a normal near point (25 cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5 cm can bring an object placed at 9.0 mm from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope.
Answer:
f = 8 mm = 0.8 cm, f = 2.5 cm
D = 25 cm, v = -D = – 25 cm, u = -9 mm = 0.9 cm

Separation between lenses

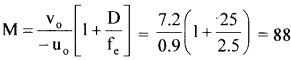
Question 13.
A small telescope has an objective lens of focal length 144 cm length 6.0 cm. What ¡s the magnifying power of the telescope between the objective and the eyepiece?
Answer:
f₀ = 144 cm, f_e = 6 cm
∴m = \(\frac{\mathrm{f}_{\mathrm{o}}}{\mathrm{f}_{\mathrm{e}}}\) = \(\frac{144}{6}\) = 24
L = f₀ + f_e = 144 + 6 = 150 cm

Question 14.
(a) A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope?
(b) If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is 3.48 ×  10⁶ m, and the radius of lunar orbit is 3.8 x 10⁸ m.
Answer:
(a) m = \(\frac{\mathrm{f}_{\mathrm{o}}}{\mathrm{f}_{\mathrm{e}}}\) = \(\frac{1500}{1}\) = 1500
(b) Diameter of moon’s image = D

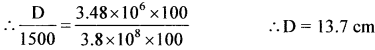
∴ D = 13.7 cm

Question 15.
Use the mirror equation to deduce that
(a) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
(b) a convex mirror always produces a virtual image independent of the location of the object.
(c) the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
(d) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Answer:
(a) \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\) ; \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\) …….(1)
f and u are negative. i.e., f< 0 and u <0.
The object is placed between land 2f, then

Using equation (1)⇒ \(\frac{1}{2f}\)<\(\frac{1}{v}\)<0 i.e., ‘v’ is negative, the image formed is real and beyond 2f.

(b) For a convex mirror, \(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) where f > 0 and u < 0, so ‘v’ is always positive. i.e., image lies on the right side of the mirror and virtual.

(c) m = \(\frac{f}{f-u}\) For a convex mirror, f is positive and u is negative.
∴ (f – u) > f i.e., m < 1
Hence the image is diminished.

(d) For a concave mirror, f < 0, u < 0.
For an object between pole and the focus, f< u <0 i.e., \(\frac{1}{f}\) – \(\frac{1}{u}\)>0
i.e., \(\frac{1}{v}\)>0
Hence v is positive and lies to the right of the pole and so the image is virtual.

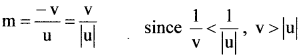
Hence ‘m’ is positive and m>1. So the image is enlarged.

Question 16.
A small pin fixed on a tabletop is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass = 1.5. Does the answer depend on the location of the slab?
Answer:
t = d[1 – \(\frac{1}{n}\)] = 15 [1 – \(\frac{1}{1.5}\)] = 5 cm. The answer is independent of the location of the slab

Question 17.
Answer the following questions:
(a) You have learnt that plane and convex mirrors produce virtual ¡mages of objects. Can they produce real ¡mages under some circumstances? Explain.

(b) A virtual image, we always say, cannot be caught on a screen. Yet when we  ‘see’ a virtual image, we are obviously bringing it on to the ‘screen’ (i.e., the retina) of our eye. Is there a contradiction?

(c) A diver underwater, looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than he actually is?

(d) Does the apparent depth of a tank of water change if viewed obliquely? if so, does the apparent depth increase or decrease?

(e) The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?
Answer:
(a) Yes. A virtual object can produce a real image.
(b) No. The lens of our eye makes a real image on the retina
(c) Taller
(d) Yes. The apparent depth of a tank of water decreases when viewed obliquely (due to refraction of light)
(e) Yes. The refractive index of diamond is 2.42 and vertical angle 24°. Any plane of the diamond. if faces with the angle of incidence > 24° can produce total internal reflection from many faces than producing a sparkling effect.

Question 18.
The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3 m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?
Answer:
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) -u + v = 3 here v = 3 + u
\(\frac{1}{3+u}-\frac{1}{u}=\frac{1}{f}\) i.e.. f = – [ \(\frac{u^{2}+3 u}{3}\) ]
For r to be maximum, \(\frac{df}{du}\) = 0
ie. \(\frac{df}{du}\) = \(\frac{1}{3}\) [2u + 3] = 0
∴u = \(\frac{-3}{2}\) ∴ v = 3 + u = 3 – \(\frac{3}{2}\) = \(\frac{3}{2}\)

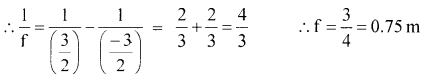
Question 19.
A screen is placed 90 cm from an object. The ¡mage of the object on the screen is formed by a convex lens at two different locations separated by 20 cm. Determine the focal length of the lens.
Answer:
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
-u + v = 90 or v = 90 + u
∴ \(\frac{1}{f}\) = \(\frac{1}{90 + u}\) – \(\frac{1}{u}\) ⇒u² + 90u + 90f = 0 ……..(1)
Let u₁ and u₂ be the values of eq. (1). Sum of the roots, u₁ + u₂ = -90 …….(2)
Product of the roots, u₁u₂ = 90 f
Also u₁ – u₂ = 20 cm ……..(3)
Equation (2) + (3) 2u₁ = – 70, u₁ = -35 cm u₂ = – 55 cm
90 f = u₁ u₂

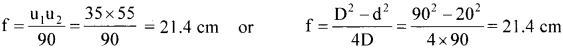
Question 20.
(a) Determine the ‘effective focal length’ of the combination of the two lenses in Exercise 9.10, if they are placed 8.0 cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of the effective focal length of this system useful at all?

(b) An object 1.5 cm in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is 40 cm. Determine the magnification produced by the two-lens system and the size of the image.
Answer:
(a) \(\frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}}\)
We have – \(\frac{1}{-\infty}+\frac{1}{v_{1}}=\frac{1}{30}\) ∴v₁ = 30 cm
The image so formed acts as an object placed at 30 – 8 22 cm from the convex lens on the right hand side.
\(\frac{1}{v_{2}}-\frac{1}{u}=\frac{1}{f_{2}}, \frac{1}{v_{2}}-\frac{1}{22}=\frac{1}{-20}\)
Solving ⇒ v₂ = -220 cm
The parallel beam of light appears to diverge from 220 – 8 = 212 cm from the convex lens from left. Now when the parallel beam of light is incident on the concave lens after which convex lens is placed at 8 cm,
\(\frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}} ; \frac{1}{v_{1}}-\frac{1}{-\infty}=\frac{1}{-20}\)
∴v₁ = -20 cm
The image is formed – 20 cm to the left of concave lens and
∴ it is 20 + 8 = 28 cm to the left of convex lens,
\(\frac{1}{v_{2}}-\frac{1}{u_{2}}=\frac{1}{f_{2}} ; \frac{1}{v_{2}}-\frac{1}{(-28)}=\frac{1}{30}\) solving v₂ = -420 cm
i.e., the light appears to diverge from a point at 420 cm to the left of a convex lens.
This shows that the answer depends on the side of incidence. So the notion of the effective focal length is not useful in this case.

(b) \(\frac{1}{v_{1}}-\frac{1}{u_{1}}=\frac{1}{f_{1}}\) \(\frac{1}{v_{1}}-\frac{1}{(-40)}=\frac{1}{30}\)
\(\frac{1}{v_{1}}=\frac{1}{30}-\frac{1}{40}=\frac{1}{120}\)
∴ v₁ = 120 cm
m₁ = \(\frac{v_{1}}{\left|u_{1}\right|}=\frac{120}{40}\) = 3
u₂ = 120 – 8= 112 cm, f₂ = – 20 cm
\(\frac{1}{v_{2}}-\frac{1}{u_{2}}=\frac{1}{f_{2}}\) \(\frac{1}{v_{2}}-\frac{1}{112}=\frac{1}{-20}\)
\(\frac{1}{v_{2}}=\frac{1}{112}-\frac{1}{20}=\frac{-23}{560}\) ∴v₂ = \(\frac{-560}{23}\) cm

m₂ = \(\frac{\left|v_{2}\right|}{u_{2}}=\frac{\left(\frac{560}{23}\right)}{112}=\frac{5}{23}\)
Net magnification. m = m₁ m₂ = \(\frac{3 \times 5}{23}\) ≈ 0.65
Size of the image = 0.98 cm

Question 21.
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524.
Answer:

sin i_c = \(\frac{1}{n}\) =\(\frac{1}{1.524}\) = 0.6562 ∴ i_c = 41°
i.e., r₂ = i_c = 41°
r₁ + r₂ = A
r₁ = A – r₂= 60 – 41 = 19°

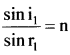
∴ sin i₁ = n sin r₁ = 1.524 sin 19° = 0.4962
i₁ = sin^-1 (0.4962) i₁ = 29°45’ ≈ 30°

Question 22.
You are given prisms made of crown glass and flint glass with a wide variety of angles. Suggest a combination of prisms which will
(a) deviate a pencil of white light without much dispersion
(b) disperse (and displace) a pencil of white light without much deviation.
Answer:
Two identical prisms made of the same glass placed with their bases on opposite sides (of the incident white light) and faces touching (or parallel) will neither deviate nor disperse, but will merely produce a parallel displacement of the beam.

(a) To deviate without dispersion, choose, say, the first prism to be of crown glass, and take for the second prism a flint glass prism of suitably chosen refracting angle (smaller than that of crown glass prism because the flint glass prism disperses more) so that dispersion due to the first is nullified by the second.

(b) To disperse without deviation, increase the angle of flint glass prism (i.e., try flint glass prisms of greater and greater angle) so that deviations due to the two prisms are equal and opposite. (The flint glass prism angle will still be smaller than that of crown glass because flint glass has higher refractive index than that of crown glass). Because of the adjustments involved for so many colours, these are not meant to be precise arrangements for the purpose required.

Question 23.
For a normal eye, the far point is at infinity and the near point of distinct vision is about 25 cm in front of the eye. The cornea of the eye provides a converging power of about 40 dioptres, and the least converging power of the eye-lens behind the cornea is about 20 dioptres. From this rough data estimate the range of accommodation (i.e., the range of converging power of the eye-lens) of a normal eye.
Answer:
Total power = 40 + 20 = 60 dioptre
u = -∞, f = \(\frac{1}{P}\) = \(\frac{1}{60}\) m,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
∴ \(\frac{1}{v}-\frac{1}{(-\infty)}\) = 60
∴v = \(\frac{1}{60}\)m = \(\frac{100}{60}\) cm
i.e, v = \(\frac{5}{3}\) cm
To focus the object at the near point, u = – 25 cm, v = \(\frac{5}{3}\) cm
∴\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) = \(\frac{3}{5}\) – \(\frac{1}{(-25)}\)
= \(\frac{3}{5}\) + \(\frac{1}{25}\) = \(\frac{15 + 1}{25}\) = \(\frac{16}{25}\)
∴Power \(\frac{1}{f}\) = \(\frac{16}{25}\) x 100 = 64 dioptres

Question 24.
A myopic person has been using spectacles of power -1.0 dioptre for distant vision. During old age, he also needs to use a separate reading glass of power + 2.0 dioptres. Explain what may have happened.
Answer:
The far point of the person is 100 cm, while his near point may have been normal (about 25 cm). Objects at infinity produce virtual images at 100 cm (using spectacles). To view closer objects i.e., those which are (or whose images using the spectacles are) between 100 cm and 25 cm, the person uses the ability of accommodation of his eye-lens. This ability usually gets partially lost in old age (presbyopia). The near point of the person recedes to 50 cm. To view objects at 25 cm clearly, the person needs converging lens of power +2 dioptres.

Question 25.
A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What ¡s this defect due to? How is such a defect of vision corrected?
Answer:
Astigmatism. This defect is removed by using a cylindrical lens with a vertical axis.

Question 26.
A man with a normal near point (25 cm) reads a book with a small print using a magnifying glass: a thin convex lens of focal length 5 cm.
(a) What is the closest and the farthest distance at which he should keep the lens from the page so that he can read the hook when viewing through the magnifying glass?
(b) What is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope?
Answer:
(a) \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\), v = – 25cm, f = 5 cm
–\(\frac{1}{25}-\frac{1}{u}=\frac{1}{5}\), –\(\frac{1}{u}\) = \(\frac{1}{5}\) + \(\frac{1}{25}\) = \(\frac{6}{25}\)
u = \(\frac{-25}{6}\) cm = -4.2 cm
To see the object at the farthest point, its image must be formed at infinity.
i.e., v = – ∞ ∴ – \(\frac{1}{u}\) = \(\frac{1}{5}\); u = -5 cm
i.e., The object is placed at 5 cm from the magnifying glass

(b) Maximurn angular magnification = m = \(\frac{D}{|u|}=\frac{25}{\left|\frac{25}{6}\right|}\) = 6
Minimum magnification = \(\frac{D}{|u|}=\frac{25}{|5|}\) = 5

Question 27.
A card sheet divided into squares each of size 1 mm² is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 9 cm) held close to the eye.
(a) What is the magnification produced by the lens? How much is the area of each square in the virtual image?
(b) What is the angular magnification (magnifying power) of the lens?
(c) Is the magnification in (a) equal to the magnifying power in (b)? Explain.
Answer:
(a) f = 10 cm, u = -9 cm
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}+\frac{1}{u}\) = \(\frac{1}{10}-\frac{1}{9}= -\frac{1}{90}\)
∴ v = – 90 cm
Linear magnification = \(\frac{v}{u}\) = \(\frac{-90}{9}\)= 10
Area of each square in the image = (1 mm x 10)² = 100 mm² = 1cm²

(b) Angular magnifìcation = \(\frac{D}{|u|}=\frac{25}{9}\) ≈ 2.8

(c) No. if the image is located near the least distance of distinct vision (v = D = 25 cm), the two quantities in (a) and (b) are equal.

Question 28.
(a) At what distance should the lens be held in Exercise 27 in order to view the squares distinctly with the maximum possible magnifying power?
(b) What is the magnification in this case?
(c) Is the magnification equal to the magnifying power in this case? Explain.
Answer:
(a) v = – 25 cm. f = 10 cm
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\),\(\frac{1}{-25}-\frac{1}{\mathrm{u}}=\frac{1}{10}\)
Solving ⇒ u = \(\frac{-50}{7}\) = – 7.14 cm

(b) Linear magnification = \(\frac{v}{u}\) = \(\frac{-25}{\left(\frac{-50}{7}\right)}\) = 3.5

(c) Yes. Angular magnification = \(\frac{D}{|\mathbf{u}|}\) = \(\frac{-25}{\left(\frac{-50}{7}\right)}\) = 3.5

Question 29.
What should be the distance between the object in Exercise 28 and the magnifying glass if the virtual image of each square in the figure is to have an area of 6.25 mm². Would you be able to see the squares distinctly with your eyes very close to the magnifier?
Answer:
New area = 6.25 mm²
∴Length of each side = 2.5 mm
linear magnification = \(\frac{1}{v}\) = \(\frac{2.5}{1}\) = 2.5
v = 2.5 u, ∴\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{2.5u}\) – \(\frac{1}{u}\)
= \(\frac{1 – 2.5}{2.5 u}\) = \(\frac{1.5}{2.5u}\) = \(\frac{1}{10}\)
i.e., u = – 6 cm
v =2.5 u = 2.5 x -6 = – 15 cm
Since \(|\mathbf{v}|\) = 1 5 cm <25 cm. The image lies at a distance less than the least distance of distinct vision and cannot be observed distinctly.

Question 30.
Answer the following questions:
(a) The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense does a magnifying glass provide angular magnification?

(b) In viewing through a magnifying glass, one usually positions one’s eyes very close to the lens. Does angular magnification change if the eye is moved back?

(c) Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?

(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?

(e) When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?
Answer:
(a) Even though the absolute image size is bigger than the object size, the angular size of the image is equal to the angular size of the object. The magnifier helps in the following way: without it object would be placed no closer than 25 cm; with it the object can be placea much closer. The closer object has larger angular size than the same object at 25 cm. It is in this sense that angular magnification is achiçved.

(b) Yes, it decreases a little because the angle subtended at the eye is then slightly less than the angle subtended at the lens. The effect is negligible if the image is at a very large distance away.
[Note: When the eye is separated from the lens, the angles subtended at the eye by the first object and its image are not equal.)

(c) First, grinding lens of very small focal length is not easy. More important, if you decrease focal length, aberrations (both spherical and chromatic) become more pronounced. So, in practice. you cannot get a magnifying power of more than 3 or so with a simple convex lens. However, using an aberration-corrected lens system, one can increase this limit by a factor of 10 or so.

(d) Angular magnification of eye-piece is [(25/f_e ) + 1] ( f_e in cm) which increases if f_e is smaller. Further, magnification of the objective is given by \(\frac{v_{0}}{\left|\mathbf{u}_{o}\right|}=\frac{1}{\left(\frac{\left|\mathbf{u}_{o}\right|}{\mathbf{f}_{0}}\right)-1}\) which is large when \(\left|\mathrm{u}_{\mathrm{o}}\right|\) is slightly greater than f₀ The microscope is used for viewing very close objects. So \(\left|\mathrm{u}_{\mathrm{o}}\right|\) is small, and so is f₀

(e) The image of the objective in the eye-piece is known as ‘eye-ring’. All the rays from the object refracted by the objective go through the eye-ring. Therefore, it is an ideal position for our eyes for viewing. If we place our eyes too close to the eye-piece, we shall not collect objects refracted by objective go through the eye-ring. Therefore, it is an ideal position for our eyes for viewing. If we place our eyes too close to the eye-piece, we shall not collect much of the light and also reduce our field of view.

If we position our eyes on the eye- ring and the area of the pupil of our eye is greater or equal to the area of the eye-ring, our eyes will collect all the light refracted by the objective. The precise location of the eye ring naturally depends on the separation between the objective and the eye-piece. When you view through a microscope by placing your eyes on one end, the ideal distance between the eyes and eye-piece ¡s usually built-in the design of the instrument.

Question 31.
An angular magnification (magnifying power) of 30 x is desired using an objective of focal length 1.25 cm and an eyepiece of focal length 5 cm. How will you set up the compound microscope?
Answer:

Solving ⇒ u₀ = – 1.5 cm and v₀ = + 7.5 cm
Then \(\frac{1}{v_{e}}-\frac{1}{u_{e}}=\frac{1}{f_{e}}\) , \(\frac{1}{-25}-\frac{1}{u_{e}}=\frac{1}{5}\)
– \(\frac{1}{u_{e}}=\frac{1}{5}+\frac{1}{25}=\frac{6}{25}\)
∴u_e = \(\frac{-25}{6}\) = – 4.2 cm
Distance between objective and eyepiece = v₀ + \(\left|\mathrm{u}_{\mathrm{e}}\right|\) = 7.5 + 4.2 = 11.7 cm
Position of the object from objective = \(\left|\mathrm{u}_{\mathrm{e}}\right|\) = 1.5 cm

Question 32.
A small telescope has an objective lens of a focal length of 140 cm and an eyepiece of a focal length of 5.0 cm. What is the magnifying power of the telescope for viewing distant objects when
(a) the telescope is in normal adjustment (i.e., when the final image is at infinity)
(b) the final image is formed at the least distance of distinct vision (25 cm)?
Answer:

Question 33.
(a) For the telescope described in Exercise 32 (a), what is the separation between the objective lens and the eyepiece?
(b) if this telescope is used to view a 100 m tall tower 3 km away, what is the height of the image of the tower formed by the objective lens?
(c) What is the height of the final image of the tower if it is formed at 25 cm?
Answer:
(a) Separation between the objective and eyepiece 140 + 5 = 145 cm

(b) Angle subtended by the tower = α

(c) Angular magnification of the eyepiece = \(\left(1+\frac{D}{f_{e}}\right)\) = 1 + \(\frac {25}{5} \) = 6
∴ Height of the final image 6h = 6 x 4.7 = 28.2 cm

Question 34.
A Cassegrain telescope uses two mirrors. Such a telescope is built with mirrors 20 mm apart. if the radius of curvature of the large mirror is 220 mm and the small mirror is 140 mm, where will the final image of an object at infinity be?
Answer:
f_e = \(\frac {220}{2} \) = 110 mm
Object at infinity forms an image at 110 cm.
This image will act as a virtual object for the smaller mirror.
Distance of virtual object from smaller mirror
u = 110 – 20 = 90 mm
f_e = \(\frac {140}{2} \) = 70 mm
Using \(\frac{1}{\mathrm{v}}+\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}_{\mathrm{s}}}\)⇒
\(\frac{1}{\mathrm{f}_{\mathrm{s}}} \Rightarrow \frac{1}{\mathrm{v}}=\frac{1}{\mathrm{f}_{\mathrm{s}}}-\frac{1}{\mathrm{u}}=\frac{1}{70}-\frac{1}{90}=\frac{1}{315}\) mm
v = 315 mm
i.e.. Final image is 315 mm from smaller mirror on the right side

Question 35.
Light incident normally on a plane mirror attached to a galvanometer coil retraces backward as shown in the figure. A current in the coil produces a deflection of 3.5° of the mirror. What is the displacement of the reflected spot of light on a screen placed 1.5 m away?

Answer:
The reflected rays get deflected by twice the angle of rotation of the mirror.
\(\frac {d}{1.5} \) tan 7° ∴d = 18.4 cm

Question 36.
The figure shows an equiconex lens (of refractive index 1.50) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid?
f = 45 cm, n = 1.5, f₁ = 30

GSEB Class 12 Physics Ray Optics and Optical Instruments Additional Important Questions and Answers

Question 1.
A convex mirror is placed in water
(a) Will there be any change in its focal length?
(b) Give reason.
Answer:
(a) No
(b) Focal length of a mirror does not depend upon the refractive index.

Question 2.
(a) Which mirror is used as a driver mirror?
(b) Why?
Answer:
(a) Convex mirror
(b) Field of view is large. Produces erect and diminished image, so that the driver can see a large part of the traffic coming from the back of the driver.

Question 3.
(a) State the law of distances.
(b) Using the law deduce that an object between F and 2F of a concave mirror produces real image beyond 2F
Answer:
(a) \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
u – Object distance
y – Image distance
f – Focal length

(b) For concave mirror, f< 0
For object. u<0
For 2f<u<f, we get \(\frac{1}{2f}\)>\(\frac{1}{u}\)>\(\frac{1}{f}\)
i.e.. –\(\frac{1}{2f}\)<-\(\frac{1}{u}\)<-\(\frac{1}{f}\)
\(\frac{1}{f}\) – \(\frac{1}{2f}\)<\(\frac{1}{f}\) – \(\frac{1}{u}\)<\(\frac{1}{f}\) – \(\frac{1}{f}\)
\(\frac{2 – f}{2f}\)<\(\frac{1}{v}\)<0
[since \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)]
i.e., \(\frac{1}{2f}\)< \(\frac{1}{v}\)<o
i.e., the Image lies on the left, beyond 2f and it is real.

Question 4.
What is the cause of the refraction of light?
Answer:
Light travels at different speeds in different media The bending or refraction of light occurs due to the change in the speed of light as it passes from one medium to another.

Question 5.
When does Such law of refraction fail?
Answer:
When the incident light is normal to the surface of separation between two media, then Snell’s law fails.
i.e., angle of incidence, i = 0° and angle of refraction, r = 0°

Question 6.
A beaker is placed on the top of a coin. Tut’ lop of ¡ht’ beaker is closed with an opaque both with a small hole. View the coin from an angle, slowly add water through the hole while continuing to view the coin from the same angle. Repeat the procedure
using cooking oil.
(a) What happens when water is continuously added?
(b) What about the heights of water and oil, when the coin completely disappears?
(c) In which liquid, the coin is concealed best with minimum height? Why?
(d) ‘hat is the relation between critical angle and refractive index?

(a) Coin appears to be raised.
(b) Height of the oil is less than that of water.
(c) Since the critical angle of oil is less than that ofter, the object disappears more easily in oil.

Question 7.
A beam of light passing from one transparent medium to another obliquely undergoes an abrupt change in direction. This phenomenon is known as the refraction of light.
(a) Name the law which satisfies during this refraction.
(b) Draw the figure which shows refraction through a parallel-sided glass slab (Ray passing from the air)
(c) Using the figure obtained in (b), show that the incident ray and the emergent ray are parallel to each other
Answer:
(a) Snell’s law.

(c) Let ABCD be a rectangular refracting glass slab PQRS is the course of ray through a parallel-sided glass slab placed in air.
Considering the refraction at face AB


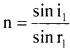
Hehce i₁ = i₂ and r₁ = r₂
We can see that the angle of incidence is equal to the angle of emergence. Thus we can conclude that the emergent ray RS ¡s parallel to incident ray PQ. but is laterally displaced.

Question 8.
You are given an equilateral glass prism of refractive index ‘n’. A light ray is an incident on of its faces at an angle ‘i₁‘.
(a) What happens when you increase ‘i ‘gradually?
(b) What happens f ‘î,’ is increased beyond a certain value?
(c) Give the graphical representation of variation.
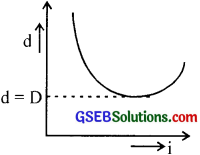
Answer:
(a) As ‘i₁‘’ increases gradually; the angle of deviation ‘d’ decreases.
(b) For a particular value of ‘i₁‘, the angle ‘d’ reaches a minimum value. If again we increase ‘i₁‘’, then ‘d’ also increases.

Question 9.
(a) What is the principle used in optical fibres?
(b) Explain briefly the working principle.
(c)What are the uses of optical fibres?
Answer:
(a) Total internal reflection
(b) Optical fibers work on the principle of total internal reflection. A fibre consists of a large number of very long fine quality glass or quartz (of higher refractive index). They are coated with a thin layer of material of lower refractive index.

When light is incident at a small angle on one end, it is refracted into the fibre and falls on the surface of the coating. Until the angle of incidence remains greater than the critical angle of fibre, it is completely reflected again and again. Then it emerges out through the other end even lithe fibre is bent.

(c) Uses

• Used as ‘light pipe’ in medical and optical diagnosis.
• Used in optical signal transmission.
• used to carry telephone, television, and computer signals as pulses of light.
• Used for transmission and receiving electrical signals which have been converted into light.

Question 10.
If the tumbler is suitably tilted and viewed at a suitable angle,
(a) how the coin appears?
(b) what is ii due to?
(c) Draw the course of the light ray.

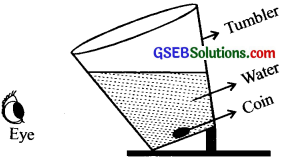
Answer:
(a) Coin floats in air Eye
(b) Due to total internal reflection.
(c)

Question 11.

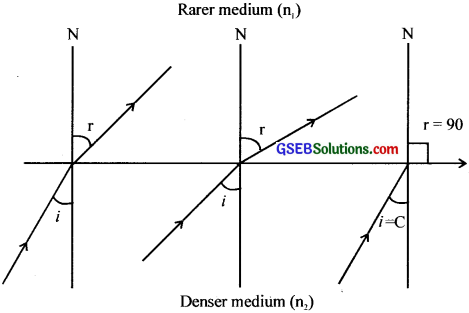
A ray of light passes from denser medium to rarer medium.
(a) What happens to the refracted ray as the angle of incidence increases from 00?
(b) What is the importance of angle C (marked in the figure above)?
(c) How is ‘C ‘related to the refractive index n’ of the medium? Explain.
Answer:
(a) The refracted ray propagates with an increased angle of refraction.
(b) At the angle of incidence ‘C’, the refracted ray just graces the surface separating the
two media Angle ‘C’ is called the critical angle.
(c) sin C = \(\frac {1}{n} \)

Question 12.
A candle ¡s placed in front of a concave lens.
(a) Draw the course of the light ray through the lens and study the nature of the image formed.
(b) Is it possible for the concave lens to form a real image?
(c) If possible draw the corresponding ray diagram.
(d) Yes. With incident beam highly converging.
Answer:

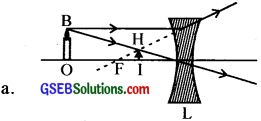
(b) Yes. With incident beam highly converging.

Question 13.
(a) What is meant by magnifìcarion m’?
(b) Give the mathematical relation.
(c) How is ‘m‘ related to object distance and ¡mage distance?
Answer:
(a) Magnification is the ratio of the size of the image to the size of the object.

Question 14.
The power of a lens is +2D.
(a) What do you mean by this?
(b) How is the power of a lens related to its focal length?
Answer:
(a) Power P = + 2D
2 = \(\frac{1}{f_{(m)}}\),
∴f_(m) = \(\frac {1}{2} \) = 0.5 m
It means power of a lens is +2 dioptres and the lens is convex lens.

P = \(\frac{1}{f_{(m)}}\),

Question 15.
You are given two convex lenses.
(a) What is the focal length of the combined lens formed by the lenses put in contact
(b) What is the advantage of the combination?
(c) if one of the lenses is concave, how will you find its focal length with, the hell) of lens combination?
Answer:
(a) \(\frac{1}{\mathrm{~F}}=\frac{1}{\mathrm{f}_{1}}+\frac{1}{\mathrm{f}_{2}}\)
F – Focal length of combination of lenses
f₁ – Focal length of one lens
f₂ – Focal length of second lens

(b) i. Increases magnifying power.
ii. For erecting an image.

(c) The focal length ‘f’ of the convex lens and ‘F’ of the lens combination can be found out by the u-v method. Let f., be the focal length of the concave lens. Then \(\frac{1}{\mathrm{f}_{2}}=\frac{1}{\mathrm{~F}}-\frac{1}{\mathrm{f}_{1}}\) Knowing f₁ and F, ‘f₂’ can be found out.

Question 16.
Why do stars twinkle?
Answer:
The continuous change in the densities of the air layer produces an unequal refractive index. So light rays from the sun while passing through air undergo refraction.. Hence to an observer, the position of the star changes continuously. Thus the stars are found to twinkle.

Question 17.
Why does a diamond sparkle?
Answer:
The Refractive index of diamond is large. Hence its critical angle is small. When faces of a diamond are cut suitably, the light rays entering through the surface undergo total internal reflections repeatedly and come through only a few faces. Hence diamond sparkles when we see the emerging light in its direction.

Question 18.
When a solar spectrum is viewed, we can see a number of dark lines.
(a) What are these dark lines called?
(b) How are they formed?
(c) What is their importance?
Answer:
(a) Fraunhofer lines
(b) The central part of the sun is called the photosphere, which is at an extremely high temperature of the order of I O’K. It is surrounded by less dense, luminous, and highly compressed gases, and they form the sun’s atmosphere. The photosphere emits radiations of all wavelengths. Surrounding the photosphere, there is another sphere of gases and vapours at a comparatively lower temperature (6000 K) called the chromosphere.

It contains certain terrestrial elements in the form of vapours. When continuous light of all wavelengths from the sun’s atmosphere passes through the chromosphere. certain wavelengths are absorbed by the elements in the chromosphere. This accounts for the presence of dark lines in the spectrum of the sun. These dark lines are called Fraunhofer lines. During a total solar eclipse. all the Fraunhofer lines turn to bright lines.

(c)The study of Fraunhofer lines establishes the presence of light gases like hydrogen, helium. oxygen, iron, sodium, calcium, etc in the outer envelope of the sun.

Question 19.
where I is the intensity of light and its wavelength.
(a) Which law does the above expression represent?
(b) Give the law in statement form.
(c) What conclusion do you draw from this?
Answer:
(a) Rayleigh’s scattering law.
(b) Intensity of scattered light is inversely proportional to the fourth power of wavelength.
(c) Shorter the wavelength larger the scattering intensity.

Question 20.
(a) What is the scattering of light?
(b) Explain Rayleigh scattering.
(c)Why sky appears blue?
(d) Sky blue extends over a wide region. Why?
Answer:
(a) The irregular reflection of light in all directions at random from extremely small particles such as dust, molecules of air etc is called scattering of light.
(b) According to Rayleigh’s scattering law, the intensity of scattered light is inversely proportional to the fourth power of the wavelength.
i.e.. Intensity,\(\text { I } \propto \frac{1}{\lambda^{4}}\)
It is found that shorter wavelengths are scattered more than longer wavelengths.

(c) The blue colour of the sky is due to the scattering of light by small particles of the atmosphere. According to Rayleigh’s scattering law, the scattering intensity is maximum for smaller wavelengths. The size of the particles in the upper atmosphere is smaller so that the radiations of shorter wavelengths are scattered with greater intensity. Sunlight is rich with blue and therefore the most intense scattered color is blue. Thus sky appears blue.

(d) Scattering of upper atmospheric particles produces blue of the sky. Since the region of observation is extended the blue colour thus extends over a wide region.

Question 21.
A piano-convex lens fits exactly into a plano-concave lens. Their surfaces are parallel to each other f the lenses cire made of different material Will the combination act as a lens? If so, what is its focal length? Is it convergent or divergent?
Answer:
Let R be the radius of curvature

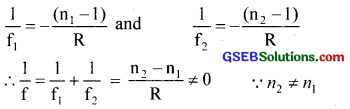
Since F has a finite value, the combination acts as a lens. It will be convergent if n₂> n₁ and
divergent if n₂ < n₁

Question 22.
The teacher shows a thin lens and a thick lens.
(a) Which of these lens forms inUre the enlarged image?
(b) Which lens has a greater focal length?
Answer:
(a) Thin lens
(b) Thin lens

Question 23.
(a) Is there any difference between fluorescence and phosphorescence?
(b) If so, what is the difference?
Answer:
(a) Yes
(b) Fluorescence is the process in which a substance absorbs the energy from radiation and emits it in a different wavelength from those absorbed. If the process continues even after the exciting radiation is removed, then the process is called phosphorescence.

Question 24.
it can be seen that no rainbow is seen during the middle of the day. Give reason.
Answer:
For viewing the rainbow, the observer must stand with his back towards the sun and look at the sky.
This is not possible during the middle of the day and hence the reason.

Question 25.
How could a blue object appear under sodium lamp light?
Answer:
The object will appear black.

Question 26.
A welder wears u mask. Give reason.
Answer:
The filter in the mask absorbs ultraviolet radiation produced by the welding ar(c)This radiation is dangerous for the eyes.

Question 27.
Sha went to a doctor and said that he could not see distant objects clearly. The doctor tested and prescribed a lens of power – 0. 75D.
(a) What is the eye defect of Sha?
(b) Why did the doctor prescribe a lens -0. 75D?
(c) What type of lens is this?
Answer:
(a) Short sight
(b) Power of lens = – 0.75 D
∴ Focal length, f = \(\frac {-1}{p} \) = \(\frac {-1}{0.75} \) = \(\frac {-100}{75} \) = \(\frac {-4}{3} \)m
A short sighted person can see only nearby objects clearly. By using a concave lens of power – 075 D, the image is made to fall on the retina
(c) The concave lens.

Question 28.
Hari asked Prof Joy, “Si, why are you using spectacles to read textbooks etc“. Prof Joy explained. What is the explanation given by Prof Joy?
Answer:
Prof. Joy is suffering from long sight and this defect is rectified by using a convex lens of suitable power. Thus he can see nearer objects clearly.

Question 29.
A point object at a distance of 36 cm from a convex lens of-focal lenth 10 cm. is moved by 10 cm in 2 sec along the principal axis towards the lens. Then image will also change its position.
(a) Write the law which relates object and image distance from the lens.
(b) Find the initial and final position of the image and calculate the average speed of the image.
(c) A man argues that the image will move uniformly at the same speed as that of the object. What is your opinion? Justify.
Answer:
(a) Lensmaker’sformula = \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
(b) \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)

(c) No. Speed of (he image is not uniform even though speed of the object changes uniformly.

Question 30.
You may observe that the fish inside the aquarium appears to be raised.

(a) What is the reason for this phenomenon?
(c) What happens to the height of the object, (that vertically stands in the aquarium) when it is observed by the fish?

• Becomes taller
• Becomes smaller
• The height dóes not change

Justify your answer.
Answer:
(a) Refraction of light
(c) Becomes taller.