GSEB Solutions Class 12 Physics Chapter 3 Current Electricity

Gujarat Board GSEB Textbook Solutions Class 12 Physics Chapter 3 Current Electricity Textbook Questions and Answers, Additional Important Questions, Notes Pdf.

Gujarat Board Textbook Solutions Class 12 Physics Chapter 3 Current Electricity

GSEB Class 12 Physics Current Electricity Text Book Questions and Answers

Question 1.
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω, what is the maximum current that can be drawn from the battery?
Solution:
E = 12V
r = 0.4 Ω
Maximum current is drawn when external resistance of the circuit is zero, i.e. R = 0
∴ \( { \quad I }_{ max }=\frac { E }{ r } =\frac { 12 }{ 0.4 } =30A\)

Question 2.
A battery of emf 10 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
Solution:
E = 10 V, r = 3 Ω, I = 0. 5 A
E = V + Ir = IR + Ir
R = \(\frac { E – Ir }{ I }\)
= \(\frac { 10-0.5×3 }{ 0.5 }\)
= \(\frac { 8.5 }{ 0.5 }\)
= 17 Ω
V = IR = 0.5 x 17 = 8.5 V

Question 3.
(a) Three resistors IΩ, 2Ω, and 3Ω are combined in series. What is the total resistance of the combination?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Solution:
(a) In series, R = R₁ + R₂ + R₃ = 1 + 2 + 3 = 6Ω

(b) V = IR, I = \(\frac { V }{ R }\) = \(\frac { 12 }{ 6 }\) = 2A
Potential drop across IΩ = V₁ = IR₁ = 2 x 1 = 2 V
Potential drop across 2Ω = V₂ = 2 x 2 = 4 V
Potential drop across 3Ω = V₃ = 2 x 3 = 6V

Question 4.
(a) Three resistors 2Ω, 4Ω, and 5Ω are combined in parallel. What is the total resistance of the combination?
(b) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor and the total current drawn from the battery.
Solution:

Question 5.
At room temperature (27.0°C) the resistance of a heating element is 100 Ω,. What is the temperature of the element if the resistance is found to be 117 Ω,. Given that the temperature coefficient of the material of the resistor is 1.70 x 1o^-4°C^-1.
Solution:
T₁ = 27°C, R₁ = 100Ω, RΩ = 117 Ω, α = 1.7 x 1o^-4°C^-1
R₁ = R₂(1+a ?T)
ΔT = \(\frac{\mathrm{R}_{2}-\mathrm{R}_{1}}{\mathrm{R}_{1} \alpha}\)
= \(\frac{117-100}{100 \times 1.7 \times 10^{-4}}\)
= 1000°
T₂ = T₁ + ΔT = 27 + 1000=1027°C

Question 6.
A negligibly small current is passed through a wire of length 15m and uniform crosssection 6.0 x 10^-7 m² and its resistance is measured to be 5.0 Ω. What is the resistivity of the material at the temperature of the experiment?
Solution:
R=5Ω, l = 115m, A = 6 x 10^-7 m²
resistivity, ρ = \(\frac { RA }{ l }\)
= \(\frac{5 \times 6 \times 10^{-7}}{15}\)
= 2 x 10^-7 Ω m

Question 7.
A silver wire has a resistance of 2.1 Ω at 27.5°C and a resistance of 2.7 ? at 100°C. Determine the temperature coefficient of resistivity of silver.
Solution:
R₁ = 2.1 Ω, T₁ = 27.5°C
R₂ = 2.7 Ω, T₁ = 100°C
α = \(\frac{\mathrm{R}_{2}-\mathrm{R}_{1}}{\mathrm{R}_{1} \cdot \Delta \mathrm{T}}\)
= \(\frac { 2.7-2.1 }{ 2.1(100-27.5) }\)
= 0.0039°C^-1

Question 8.
A heating element using nichrome connected to a 230V supply draws an initial current of 3.2 A which settles after a few seconds to steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0°C? The temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70 x 10^-4°C^-1.
Solution:

Question 9.
Determine the current in each branch of the network shown in Fig.

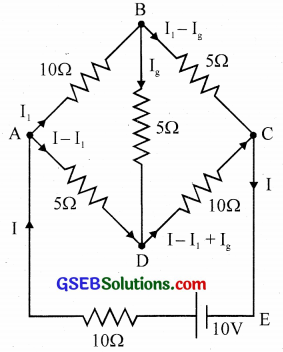
Solution:
For the mesh \(\overrightarrow{\mathrm{ABDA}}\), 10I₁ + 5I_g – 5(I – I₁) = 10
15I₁ + 5I_g – 5I = 0
3I₁ + I_g – I = 0 …. (1)
For the mesh \(\overrightarrow{\mathrm{BDCB}}\),
5I_g + 10(I – I₁+I_g) – 5(I₁ – I_g) = 0
– 15I₁ + 20I_g + 10I = 0
i.e., 3I₁ – 4I_g – 2I = 0 … (2)
For the mesh \(\overrightarrow{\mathrm{ABCEA}}\), 10I₁ + 5(I_g – (I – I₁ + 101 = 10
15I₁ – 5I_g + 10I = 10
3I₁ – I_g + 10I = 10 …. (3)
Equation (1) + (3) ⇒, 6I₁+ I = 2 …. (4)
Equation (1) x 4 + (2) ⇒ 15I₁ – 6I = 0 …. (5)
Solving equation (4) and (5) ⇒ I₁ = \(\frac { 4 }{ 17 }\) A and I = \(\frac { 10 }{ 17 }\)
Substituting for I₁ and I in equation (3) ⇒ I_g = – \(\frac { 2 }{ 17 }\)A
The negative sign shows that the direction of current in the branch BD is opposite to that shown in the figure.
Current through AB = \(\frac { 4 }{ 17 }\) A
Current through BC = \(\frac { 6 }{ 17 }\) A
Current through AD = \(\frac { 6 }{ 17 }\) A
Current through DC = \(\frac { 4 }{ 17 }\) A
Current through BD = – \(\frac { 2 }{ 17 }\) A

Question 10.
(a) In a metre bridge the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5 Ω. Determine the resistance of X. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips?
(b) Determine the balance point of the bridge if X and Y are interchanged.
(c) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?

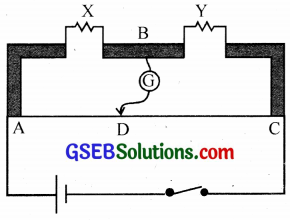
Solution:
(a) \(\frac { X }{ Y }\) = \(\frac { l }{ 100 – l }\)
\(\frac { X }{ 12.5 }\) = \(\frac { 39.5 }{ 60.5 }\)
∴ X = 8.16 Ω
Thick wires minimise the resistance of the connections and hence they will not affect the bridge formula.

(b) \(\frac { Y }{ X }\) = \(\frac { l’ }{ 100 – l’ }\)
\(\frac { 12.5 }{ 8.16 }\) = \(\frac { l’ }{ 100 – l’ }\)
Solving we get, l’ = 60.5 cm

(c) The galvanometer will not show any current.

Question 11.
A storage battery, of emf 8.0 V and internal resistance 0.5 Ω is being charged by a 120 V dc supply using a series resistor of 15.5 Ω. What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?
Solution:
r = 0.5 Ω, R = 15.5 Ω
when the storage battery emF 8 V is charged with a d.c supply of 120V the net EMF of the circuit
E= 120 – 8 = 112V
Therefore the current in the circuit during charging,
\(I=\frac { E }{ R+r } =\frac { 112 }{ 15.4+0.5 } =7A\)
The terminal voltage of the storage battery would be equal to the sum of its EMF and the potential difference across its internal resistance i.e. terminal voltage = 8 + 0.5 x 7 = 11.5 V

Question 12.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell?
Solution:
E ∝ l
\(\frac{\mathrm{E}_{1}}{\mathrm{E}_{2}}\) = \(\frac{\mathrm{l}_{1}}{\mathrm{l}_{2}}\)
∴ E₂ = \(\frac{\mathrm{l}_{2}}{\mathrm{l}_{1}}\) x E₁ = \(\frac { 63 }{ 35 }\) x 12.5
i.e., E₂ = 2.25 V

Question 13.
The number density of free electrons in a copper conductor is 8.5 x 10²⁸ m^-3. How long does an electron take to drift from one end of a wire of 3.0 m long to its other end? The area of cross-section of the wire is 2.0 x 10^-6 m² and it is carrying a current of 3.0 A.
Solution:
I = 3A
n = 8.5 x 10²⁸ m³
e = 1.6 x 10^-19 C
A = 2 x 10^-6 m²
l = 3 m

Question 14.
The earth’s surface has a negative surface charge of 10^-9 Cm^-2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth = 6.37 x 10⁶m.)
Solution:
σ = 10^-9 Cm^-2
V = 400 x 10³
I = 1800 A
R_e = 6.37 x 10⁶m
Total charge, Q = πR²_e σ

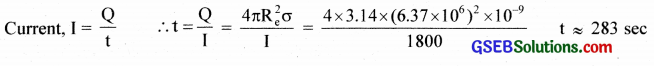
Question 15.
(a) Six lead-acid type of secondary cells each of emf 2.0 V and internal resistance 0.015 Ω are joined in series to provide a supply to a resistance of 8.5 Ω. What is the current drawn from the supply and its terminal voltage?

(b) A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
Solution:

The cell cannot drive the starting motor of the car.

Question 16.
Two wires of equal length, one of aluminium and the other of copper have the same resistance. Which of the two wires is lighter? Hence explain why aluminium wires are preferred for overhead power cables. (ρ_Al = 2.63 x 10^-8Ωm, ρ_cu = 1.72 x 10^-8Ωm, Relative density of Al = 2.7 and that of Cu = 8.9.)
Solution:

∴ Aluminium is lighter than copper. Since Al is lighter, it is preferred for overhead power cables.

Question 17.
What conclusion can you draw from the following observations on a resistor made of alloy manganin?

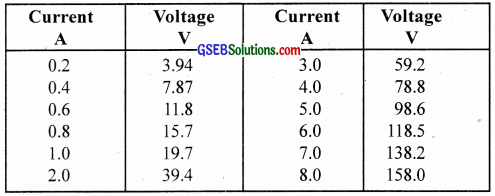
Solution:
This represents Ohm’s Law.
The resistivity of manganin remains almost the same with the change in temperature.

Question 18.
Answer the following questions.
(a) A steady current flows in a metallic conductor of the non-uniform cross-section. Which of these quantities is constant along the conductor – current, current density, electric field, drift speed?
(b) Is Ohm’s law universally applicable for all conducting elements? If not, give examples of elements which do not obey Ohm’s law.
(c) A low voltage supply from which one needs high currents must have very low internal resistance. Why?
(d) A high tension (HT) supply of, say, 6 kV must have a very large internal resistance. Why?
Solution:
(a) Except current the values of all the other quantities depend upon the area of cross-section of the conductor. Hence, only current remains constant, when it flows through a conductor of the non-uniform area of cross­section.

(b) No, ohm’s law is not obeyed by all the elements. For example, vacuum diode tube and semiconductor diode.

(c) The maximum current that can be drawn from a voltage supply is given by,
\({ I }_{ max }=\frac { E }{ r } \) Obviously, \({ I }_{ max }\) will be large, if r is small.

(d) If the circuit containing the H.T supply gets short-circuited accidently, the current in the circuit will not exceed the safe limit, in case the internal resistance of the H.T supply is very large.

Question 19.
Choose the correct alternative:
(a) Alloys of metals usually have (greater/less) resistivity than that of their constituent metals.
(b) Alloys usually have much (lower/higher) temperature coefficient of resistance than pure metals.
(c) The resistivity’ of the alloy manganin is nearly independent of/increases rapidly with increase of temperature.
(d) The resistivity’ of a typical insulator (e.g., amber) is greater than that of a metal by a factor of the order of (10²²/10³).
Solution:
(a) greater
(b) lower
(c) nearly independent
(d) 10²²

Question 20.
(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum effective resistance?
(b) Given the resistances of 1Ω, 2Ω, 3Ω. How will you combine them to get an equivalent resistance of (i) (11/3) Ω (ii) (11/5)Ω, (iii) 6Ω, (iv) (6/11)Ω?
(c) Determine the equivalent resistance of networks shown in the figure.

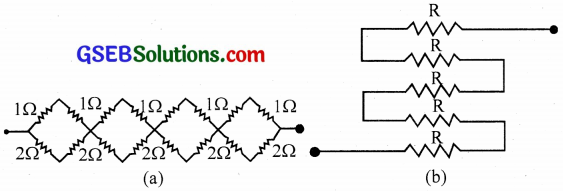
Solution:
(a)

(b) R₁Ω = 10, R₂ = 2Ω, R₃ = 3Ω
i. (R₁||R₂) series with R₃

(c) The network takes the form
i. R = (1 + 1) || (2 + 2) + (1 + 1)|| (2 + 2) + (1 + 1) || (2 + 2) + (1 + 1) || (2 + 2)
= \(\left(\frac{2 \times 4}{2+4}\right)\) x 4
= \(\frac { 8 }{ 6 }\) x 4
= \(\frac { 16 }{ 3 }\)Ω

ii. Being series, R = R + R + R + R + R = 5 R

Question 21.
Determine the current drawn from a 12V supply with internal resistance 0.5 Ω by the infinite network shown in figure. Each resistor has 1Ω resistance.

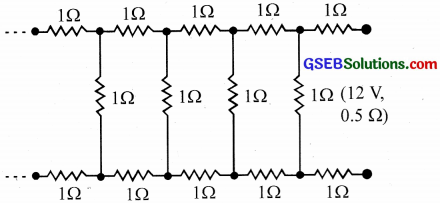
Solution:
The circuit is redrawn as follows.
Y is the equivalent resistance. Adding the resistance values of these resistors will not change the value of ‘Y’ being infinite resistors.

Question 22.
Figure shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 Ω maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for very moderate currents upto a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of 600 kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf and the balance point is found similarly, turns out to be at 82.3 cm length of the wire.

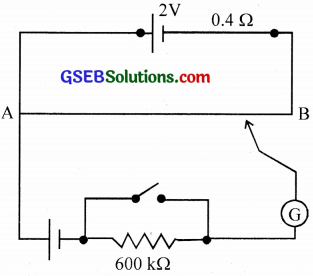
(a) What is the value ε?
(b) What purpose does the high resistance of 600 k Ω have?
(c) Is the balance point affected by this high resistance?
(d) Is the balance point affected by the internal resistance of the driver cell?
(e) Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V?
(f) Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermo-couple)? If not, how will you modify the circuit?
Solution:
(a) E ∝ l ∴ \(\frac { ε }{ 1.02 }\) = \(\frac { 82.3 }{ 67.3 }\)
ε = 1.25 V

(b) The purpose of using high resistance is to allow only a very small current to flow through the galvanometer when the balance point has not been obtained.
(c) No, the balance point is not affected by the internal resistance of the driver cell.
(d) No, the arrangement will not work. If the emf of the driver cell is less than that of the cell whose emf is to be found, the balance point will not be obtained.
(e) The circuit is not suitable for measuring extremely small emf. It is because in such a case, the balance point will be just close to end A.

Question 23.
Figure shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor R = 10.0 Ω is found to be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X. What might you do if you failed to find a balance point with the given cell of emf ε?

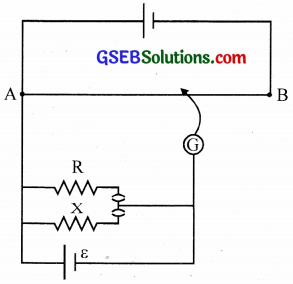
Solution:
\(\frac { R }{ X }\) = \(\frac{l_{1}}{l_{2}}\)
X = R \(\frac{l_{2}}{l_{1}}\) = \(\frac { 10 × 68.5 }{ 58.3 }\) ≈ 11.75 Ω

Question 24.
Figure shows a 2.0 V potentiometer used for the determination of internal resistance of a 1.5 V cell. The balance point of the cell in the open circuit is 76.3 cm. When a resistor of 9.5 Ω is used in the external circuit of the cell, the balance point shifts to 64.8 cm length of the potentiometer wire. Determine the internal resistance of the cell.

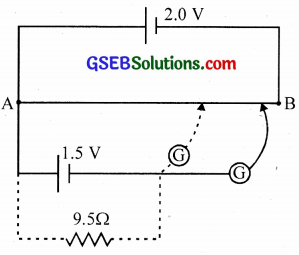
Solution:
Internal resistance, r = \(\frac { (E-V)R }{ V }\)
r = \(\frac{\left(l_{1}-l_{2}\right) \mathrm{R}}{l_{2}}\)
l₁ = 76.3 cm, l₂ = 64.8 cm, R = 9.5 Ω ∴ r = \(\frac{(76.3-64.8) \times 9.5}{64.8}\)
r = 1.686 Ω

GSEB Class 12 Physics Current Electricity Additional Important Questions and Answers

Question 1.
What do you mean by the steady current?
Answer:
A steady current is that in which the intensity of current remains constant.

Question 2.
What do you mean by the varying current?
Answer:
A varying current is the one in which the intensity of current does not remain constant.

Question 3.
In a steady flow, if charge q is flowing through a conductor for a time t, what is the charge flowing per unit time?
Answer:
Charge flowing per unit time, \(\frac { q }{ t }\)

Question 4.
In a varying flow, if ∆q is the charge flowing in a time ∆t, within the limit ∆t → 0, what is the electric current?
Answer:

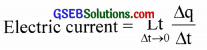
Question 5.
What is the unit of currency?
Answer:
ampere

Question 6.
Current through a conductor is said to be 1 C/s. What does it mean?
Answer:
It means that in one-second charge flowing through a conductor is one coulomb.

Question 7.
Why does current become a scalar quantity?
Answer:
Currently does not obey vector addition principle, i.e., the sum of currents always remains the same, whatever be the angle between conductors and carrying current

Question 8.
If I is the current passing normal to an area A, what is current per unit area?
Answer:
Current per unit area \(\hat { j }\) = \(\frac{\mathrm{I}}{\overrightarrow{\mathrm{A}}}\) = σ\(\vec { E }\)

Question 9.
What do you mean by current density?
Answer:
Current density is the current flowing through the unit area.

Question 10.
Why is current density a vector quantity?
Answer:
\(\hat { j }\) = σ\(\hat { E }\), since \(\hat { E }\) , the field is a vector, current density’ is also a vector.

Question 11.
The free electrons inside a metallic conductor are in random motion. Can we detect current in the conductor?
Answer:
No. In random motion, the average velocity is zero.

Question 12.
What is the essential condition for current flow in a conductor?
Answer:
When a potential difference is applied across the conductor, an electric field is set up and electrons begin to make directed flow and hence there is a current.

Question 13.
How can you produce a net flow of electric charges [electric current] in a conductor?
Answer:
By applying a p.d. Under the action of the electric field applied, electrons make drift motion and this produces current.

Question 14.
When an electric field (E) is applied to the conductor, what is the force experienced by an electron?
Answer:
Force = -eE, where ‘e’ is the charge of an electron.

Question 15.
If ‘m’ is the mass of an electron, what is its acceleration?
Answer:
Acceleration, a = \(\frac { – eE }{ m }\)

Question 16.
In the electric field, what happens to the motion of the electrons?
Answer:
Electrons flow in a direction opposite to the electric field.

Question 17.
The number density of conduction electrons in a conductor is 8.5 x 10²⁸m^-3. The area of cross-section is 10^-6m² and I = 3A.
(a) What is the drift velocity of electrons?
(b) Compare the drift velocity of electrons with thermal velocity.
(c) What is the time taken by an electron to drift from one end of the conductor 3m long to the other end?
(d) The time taken by an electron to travel in a conductor is very large. But when we switch on an electric circuit, there is no time delay to complete the circuit. Why?
Answer:
n = 8.5 x 10²⁸m^-3, I = 3A, A = 10^-6m², e = 1.6 x 10^-19C
(a)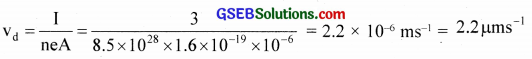
(b) Thermal speed is of the order of 10⁵ ms^-1. So the drift velocity is very very small.
(c)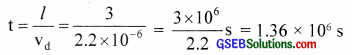
(d) Current is a circuit which will be established at the speed of propagation of electric field (speed of light)

Question 18.
(a) How can you measure the voltage across resistance and current through the circuit?
(b) How can you modify the given circuit to measure voltage across resistance and current through the circuit?

Answer:
(a) Use voltmeter to measure voltage across the resistance and ammeter to measure the current.
(b)

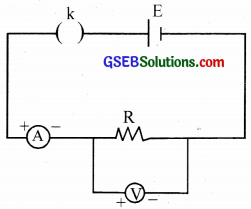
Question 19.
Why is an ammeter connected in series and a voltmeter in parallel?
Answer:
Ammeter is a low resistance instrument. Hence if ammeter is put in series, it allows the entire current to flow through it and we can measure the current in the circuit.

Question 20.
Without replacing the source, how can you vary the potential difference across the resistance wire?

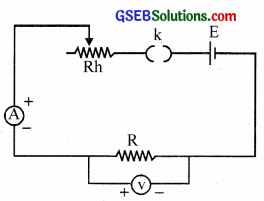
Answer:
In the circuit, introduce a rheostat. With the help of rheostat, we can vary the potential difference across the resistance wire.

Question 21.
How can you state the relation between V and I as a law?
Answer:
By Ohm’s law, V = IR

Question 22.
What is conductance?
Answer:
Conductance is the reciprocal of resistance.

Question 23.
What is the variation of resistance with length and area of cross-section of the conductor?
Answer:
Reel and R ∝ l and R ∝ \(\frac { l }{ A }\)

Question 24.
What is the relation between drift velocity and relaxation time?
Answer:
Drift velocity = v_d
Relaxation time = τ
v_d = \(\frac { l }{ A }\) = \(\frac { eE τ }{ m }\)

Question 25.
What are the relation between the electric field, length of the wire, and the potential difference between the conductor?
Answer:

Question 26.
What is the relation between resistivity and relaxation time?
Answer:
Resistivity ρ = \(\frac{\mathrm{m}}{\mathrm{ne}^{2} \tau}\)

Question 27.
When the temperature increases, what happens to relaxation time?
Answer:
Relaxation time ( τ ) decreases.

Question 28.
When relaxation time decreases, what happens to resistivity?
Answer:
Resistivity increases
ρ = \(\frac { RA }{ l }\) and R ∝ \(\frac { 1 }{ τ }\)

Question 29.
What is the variation of resistivity with temperature?
Answer:
Resistivity, ρ = ρ₀(1 + α t) for conductors where ‘ α ’ is the temperature coefficient of resistance and ‘t’ the temperature change. So resistivity increases with increase in temperature.

Question 30.
What happens to the resistivity of a conductor when the temperature becomes absolute zero or 0°K?
Answer:
Resistivity disappears.

Question 31.
What is superconductivity?
Answer:
In 1911, the Dutch Physicist, Kamerlingh Onnes established experimentally that certain metals and alloys lose their resistance at a very low temperature. He observed that when purified mercury is cooled, its resistivity disappears abruptly at 4.2 K. Above this temperature, the resistivity is small, but finite. This new phenomenon observed by Onnes is called superconductivity. The phenomenon is exhibited by a number of elements and many alloys.

Question 32.
How can you define temperature coefficient of resistance?
Answer:
Temperature coefficient of resistance (a) is defined as the ratio of increase in resistance to the original resistance per degree rise of temperature.

Question 33.
When the current in the conductor is high, what happens to the conductor?
Answer:
Conductor gets heated up.

Question 34.
What is an ohmic resistance?
Answer:
The resistance obeys Ohm’s law.

Question 35.
What is a non-ohmic resistance?
Answer:
The resistance does not obey Ohm’s law.

Question 36.
Ohm’s law is not a universal law. Why?
Answer:
It is an experimental law.

Question 37.
In parallel combination, what is the potential difference across each resistor?
Answer:
Potential difference across each resistor is the same.

Question 38.
(a) What is the effective resistance between A and C?
(b) How much current enters the circuit through A?
(c) What is the current through each resistor?
(d) What is the amount of current leaving point A?
(e) What is the potential difference between points A and C?
(f) How much emf is applied?
(g) What is the value of the potential at B?
(h) What is the value of potential at D?
(i) How much current flows through a galvanometer if it is connected between B and D?
(j) If the resistor between A and D is replaced by 2Ω, what happens to galvanometer deflection?
(k) Can you again reduce the deflection to zero by adjusting resistance between D and C?

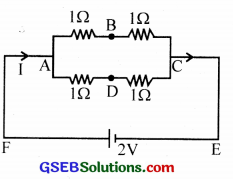
Answer:

d. 1 A through AB and 1 A through AD
e. Potential difference across AC = 2V
f. Emf is applied across the combination (between A and C)
g. Potential at B = 1 V [ \(\frac { 2 }{ 1+1 }\) ]
h. Potential at D = 1 V
i. Since V_B = V_D = 1 V, no current flows through the galvanometer connected between B and D.
j. Galvanometer shows a deflection.
k. If we put a resistance 2Ω between D and C, then we can reduce the deflection to zero in the galvanometer.

Question 39.
(a) What is the general value of the potential at B?
(b) What is general value of potential at D?
(c) What is the condition to obtain zero deflection in the galvanometer?

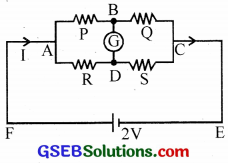
Answer:
(a) V_B = ( \(\frac { V }{ P+Q }\) )Q
(b) V_D = ( \(\frac { V }{ R+S }\) )S
(c) V_B = V_D

Question 40.
(a) What is the total resistance in the given circuit?
(b) What is the current in the circuit?

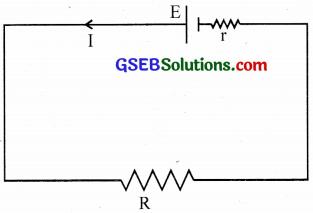
(c) What is the potential difference across the terminals of the cell?
(d) Is it equal to the emf of the cell?
(e) Find the condition under which potential difference and emf are equal?
Answer:
(a) Total resistance = R + r
(b) I = \(\frac { E }{ R+r }\)
(c) Potential difference across the terminals of the cell = V_r = \(\frac { Er }{ R+r }\)
(d) No
(e) If the internal resistance of the cell is zero or negligible, then potential difference and emf are equal

Question 41.
How can you compare the emf of two cells?
Answer:
Using potentiometer we can compare the emf of two cells.

Question 42.
What is meant by the internal resistance of a cell?
Answer:
Internal resistance of a cell is defined as the resistance offered by the components inside it to the flow of current. The value of internal resistance is low for a freshly prepared primary cell.

Question 43.
Pick the odd one out of the following.
(a) Ohm’s law
(b) Lenz’s law
(c) Coulombs law
(d) Gauss ’ law
(e) Faraday’s law
Answer:
(a) Ohm’s law

Question 44.
The following question consists of two statements each, printed as assertion and reason. While answering these questions you should choose any one of the following responses.
Assertion: In a simple battery circuit, the point at the lowest potential is the positive terminal of the battery.
Reason: The electron flows from higher potential to lower potential.
(a) Both the assertion and reason are true and the reason is a correct explanation of the assertion.
(b) Both the assertion and reason are true but the reason is not a correct explanation of the assertion.
(c) Assertion is true but the reason is false.
(d) Both the assertion and reason are false.
Answer:
(d) Both the assertion and reason are false.

Question 45.
Match the following

Answer:

Question 46.
Fill in the blanks using the words given in the brackets.
[Free electrons, free holes, drift speed, relaxation time, Ohm’s law’, critical temperature, zero temperature, r.m.s speed, super temperature, negative, Coulomb’s law, time constant]
In a metallic conductor electric current is due to the movement of …….(i)….. Metallic conductors obey ….(ii)….. In superconductors, the resistance drops suddenly to zero at a sufficiently low temperature called ..(iii)… Metals have ….(iv)… temperature coefficient of resistance.
Answer:
(i) Free electrons
(ii) Ohm’s law
(iii) critical temperature
(iv) positive

Question 47.
Match the following

Answer:

Question 48.
(a) S.I unit of elective current is ampere. Then what do you mean by saying current is one ampere?
(b) Give the relation between electric current and current density and their respective units?
Answer:
(a) Current is said to be one ampere if one-coulomb charge drifts through any cross-section of the conductor per sec.
(b) Current density \(\hat { j }\) = \(\frac { I }{ A }\), i.e., current through unit area. Current -ampere, current density – ampere/m²

Question 49.
(a) Name the factors on which resistance of a conductor depends on.
(b) For a given conductor and at a given temperature how the resistance depends on
i. its length
ii. its area of cross-section
iii. From the above derive an expression for resistivity.
Answer:
(a) The resistance of a conductor depends upon the nature of the material of the conductor, its shape, size and temperature.
To enumerate, the resistance of a conductor depends on its
i. length
ii. area of cross-section
iii. nature of the material
iv. temperature

(b)
i. R ∝ l
ii. R ∝ \(\frac { 1 }{ A }\)
iii. ∴ Resistance R ∝ \(\frac { l }{ A }\) or R = ρ\(\frac { l }{ A }\)
∴ \(\frac { R.A }{ l }\)

Question 50.
(a) Is Ohm’s law applicable to all elements? If not give example.
(b) Is e.m.f. a force or some other physical quantity?
(c) Define e.m.f
(d) What is the source of e.m.f. in a primary cell?
Answer:
(a) No. It does not strictly hold good in semiconductors, electrolytes (not all) etc. Ohm’s law is not a general law of conductors. All metallic conductors obey Ohm’s law and they are called Ohmic conductors. If we study the volt-ampere (V – I) characteristic of such metallic conductors, the graph is linear.

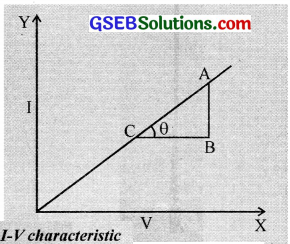
The slope, tan θ = \(\frac { AB }{ BC }\)
∴ Resistance, R = \(\frac { 1 }{ tanθ }\)
i.e, The reciprocal of the slope gives the resis tance.

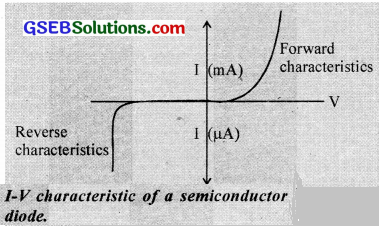
But there are many other substances, such as vacuum tubes. semiconductors, some electrolytes, etc, which do not obey Ohm’s law, and they arc called non-Ohmic conductors. The V.I. characteristic of a semiconductor diode is shown below.

The non-Ohmic conductors have the following properties.

• The relation between V and I is not linear.
• The relation between V and I depends on the sign of V.
• The relation between V and I is not unique. i.e., I may have more than one value for a given value of V.

(b) It is the energy.

(c) Energy required to circulate unit charge once round an electric circuit. It is also equal to the maximum potential difference available across the electrodes of a cell when no current is drawn from it.

(d) Chemical energy

Question 51.
A cell of emf 1.5 V and internal resistance 0.5 Ω is connected to a (non-linear) conductor whose V – I graph is shown in figure. Obtain graphically the current drawn from the cell and its terminal voltage.

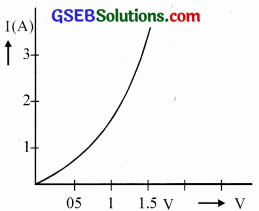
ε = 1.5 r = 0.5. Let I be the current
∴ ε – IR = I x r i.e., ε – V = Ir
i.e., 1.5 – V = I x 0.5 ……….. (1)
When V= 1.5 V, I = 0
When V = 0 V, I = 3 A
Plot a straight line graph for (1). One intersection forms the operating voltage (≈ 0.9 V) and current 1.2 A. (The graph may be reproduced on a graph paper)

Question 52.
The resistivity of copper, constantan and silver are 1.7 x 10^-6 Ω cm, 39.1 x 10^-6 Ω cm and 10^-6 Ω cm respectively.
(a) Which is the best conductor?
(b) Give reason for your answer.
(c) Define resistivity.
(d) Which material is used for potentiometer wire? Why?
Answer:
(a) Silver
(b) p – resistivity being least
(c) Resistivity of the material of a conductor is defined as the resistance of the conductor of unit length and of unit area of cross-section, or Resistivity is the resistance of unit volume of the resistor.
(d) Constantan. Its temperature coefficient of resistance is very small. (ρ is nearly independent of temperature variations)

Question 53.

1. If a person touches a live wire, will he get stuck to it?
2. Why do we use copper wires as connecting wires?
3. A wire is carrying a current. Is it charged? If not, why?

Answer:

1. Sometimes. Even very small currents are enough to disorganise our nervous system. Hence the affected person may temporarily lose his ability to exercise his nervous control to free himself from high voltage points.
2. A good conductor, low resistivity, and can be shaped to any size.
3. No. The net charge in the wire is zero even in the conducting state.

Question 54.
Light from a bathroom bulb gets dimmer for a moment when Geiser is switched on. Why?
Answer:
Since the resistance of the geiser is less than that of a bulb, geiser draws more current from the mains than the bulb. So the bulb becomes dimmer for a moment when Geiser is switched on.

Question 55.

In the above figure, the numbers 1, 2, 3 and 4 have got some meaning.
(a) What is the meaning of each number?
(b) Why is such a system used?
Answer:
(a) The first coloured band (1) gives the first significant figure, second coloured band (2) gives second significant figure, third coloured band represents multiplier (powers of ten) and the fourth coloured band gives the tolerance. Tolerance tells us how much variation can be there in the resistance value when put in use. If there is no fourth coloured band, the body colour should be considered as 20% tolerance. It means that the resistance value can vary by ± 20% of its value.

(b) Body of resistors may be big or small. If the body of a resistor is small, it is difficult to print the resistance value on it. Also, there should be a universally accepted standard for measuring resistance. Hence for convenience, colour coding system is used.

Question 56.
Two potentiometers are shown in figures (P₁) and (P₂. The first one has a 6 m length and the second one 10 m.

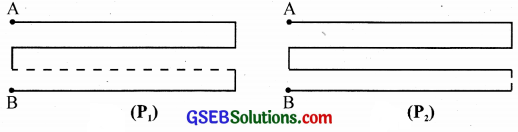
(a) Which one you prefer while finding the internal resistance of a primary cell? Why?
(b) Will the balance point be affected by the internal resistance of the given cell?
(c) Suppose you connect the two potentiometers in series, will the combination give you a better accuracy?
(d) What important precaution you should take while using the modified connection mentioned in (c)?
Answer:
(a) The one with a length 10 m: It is more sensitive
(b) No.
(c) Yes
(d) They should be of same resistance/unit length.

Question 57.
What is conventional current?
Answer:
The current which flows from the positive to negative end of a cell in the external circuit is called conventional current.

Question 58.
What is the significance of the direction of the current?
Answer:
The direction of the conventional current is opposite to the flow of electrons. The direction of electronic current is in the direction of the flow of electrons.

Question 59.
How does drift velocity of electrons in a metallic conductor vary with temperature?
Answer:
The drift velocity of electrons in a metallic conductor decreases with an increase in temperature.

Question 60.
How is p.d (V) related to drift velocity (v_d)?
Answer:

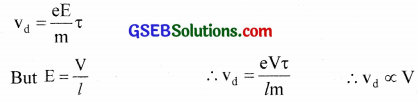
Question 61.
Define resistivity.
Answer:
The resistance offered by the unit volume of a conductor is defined as the resistivity.

Question 62.
Why are connecting wires made of copper?
Answer:
Copper has very low resistivity (high conductivity). Also copper is a diamagnetic material, so it is not magnetised due to the flow of current.

Question 63.
What is a thermistor?
Answer:
A heat-sensitive resistor whose resistance varies appreciably with temperature is known as a thermistor.

Question 64.
A wire is carrying current. Is it charged? Give reason.
Answer:
No. Current is the flow’ of free electrons in the conductor. At any instant, the number of electrons leaving the wire and that flowing from the battery to the wire is always same and hence the net charge is zero.

Question 65.
Two wires of equal lengths, one of copper and the other of manganin have equal resistance values. Which wire is thicker? Explain.
Answer:
Copper – resistivity = ρ₁, Area of cross section = A₁
Manganin – Resistivity = ρ₁, Area of cross section = A₂

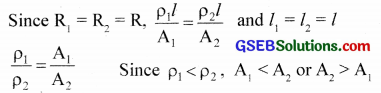
i.e,, Manganin wire is thicker.

Question 66.
Give the colour code of 240 MΩ of 10%
Answer:
240 MΩ = 240 x 10⁶ Ω = 24 x 10⁷ Ω
∴ colour code for 2 → Red
colour code for 4 → Yellow
colour code for 2 → Violet
colour code for 2 → Silver (Tolerance)

Question 67.
Two students X and Y perform an experiment on a potentiometer separately using the circuit diagram shown here. Keeping other things unchanged
(i) X increases the value of resistance R.
(ii) Y decreases the value of resistance S in the setup.

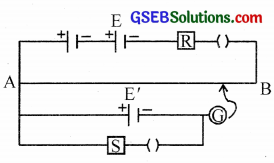
How would these changes affect the position of a null point in each case and why
Answer:
(i) When the value of resistance R is increased, then the current from the driver cell decreases in the potentiometer, the potential gradient across the wire decreases. Due to this, the balance point is shifted towards the right.

(ii) When the value of resistance S is decreased, the current in the potentiometer increases. Due to this, the balance point is shifted towards left.

Question 68.
A voltage of 30V is applied across a carrying resistor with first, second, and third rings of blue, black, and yellow colours respectively. Find the value of current through the resistor?
Answer:

Question 69.
One end of an aluminium, n wire whose diameter is 3 mm is welded to one end of a copper wire of diameter 2 mm. The composite wire carries a steady current of 20 mA. What is the current density in each wire?
Solution:
Data supplied,
For Al, radius r₁ = 1.5 mm = 1.5 x 10^-3 m
For Cu. radius r₂ = 1 mm = 1 x 10^-3 m
Current. I = 20 mA = 20 x 10^-3 A

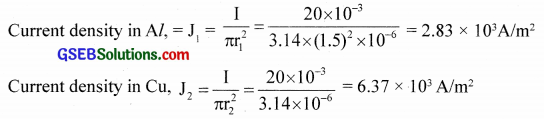
Question 70.
Twelve equal resistors each of resistance 12 Q form edges of a cube as shown. A battery of emf 24 volts is connected across the diagonally opposite corners of this cube. Determine the equivalent resistance and current through each edge.
Solution:

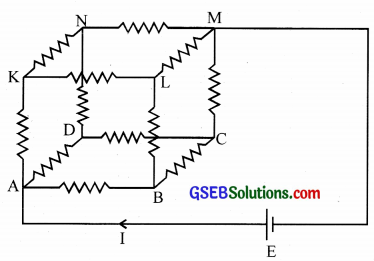
By symmetry, the current through the paths AB, AD & AK is equal to \(\frac { I }{ 3 }\). In the same way, current through the paths BC, BL, DC, DN, KL, KN is equal to \(\frac { I }{ 6 }\) and through the paths CM, LM, NM is equal to \(\frac { I }{ 3 }\). Let R_eq be the equivalent resistance.

Using Kirchhoff’s voltage law for the mesh \(\overrightarrow{\mathrm{ABCMEA}}\), \(\frac { I }{ 3 }\) x AB + \(\frac { I }{ 6 }\) BC + \(\frac { I }{ 3 }\) CM = E
i.e., \(\frac { I }{ 3 }\)R + \(\frac { IR }{ 6 }\) + \(\frac { IR }{ 3 }\)

Hence current through the branches, AB, AD, AK and CM, LM, NM = \(\frac { 2.4 }{ 3 }\) = 0.8 A and through BC, BL, DC, DN, KL & KN = \(\frac { 2.4 }{ 6 }\) = 0.4 A

Question 71.
12 cells, each having the same emf are connected in series and are kept in a closed box. Some of the cells are wrongly connected. The battery is in series with an ammeter and two cells of identical nature to others. The current is 3A when external cells aid the battery and 2A when they oppose. How many cells are wrongly connected in the battery?
Solution:
A reverse cell decreases the emf by 2 ε. Let ‘n’ cells be in opposition, then in the first connection 12ε – 2nε + 2ε = 3R
14ε – 2 nε = 3R … (1) where R is the effective resistance of the closed circuit. Similarly in opposition with external cells, 12 ε – 2nε – 2ε = 2R
i.e., 10ε – 2nε = 2R … (2)
28 – 4n = 30 – 6n
∴ 2n = 2           ∴ n = 1

Question 72.
A cell of emf E and internal resistance r is connected to an external resistance R. Show that at maximum power transfer, R = r.
Solution:

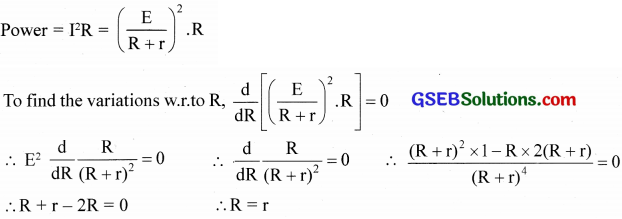
Question 73.
One section AB of a circuit absorbs 53.0 W of power when a current i = 1.20 A passes through it in the direction shown.
(a) Find the potential difference between A and B.
(b) If element C does not have an internal resistance, what is its emf?
(c) Which terminal left or right is positive?

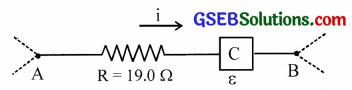
Solution:
Let ‘r’ be the internal resistance of C. The power relation is
i²(R + r) = 53.0 But R = 19.0 and i = 1.20 A
r = \(\frac{53.0}{(1.2)^{2}}\) – 19.0 = 17.8 Ω

(a) p.d between A and B is i(R + r) = 1.2 (19 + 17.8) = 44.2 V

(b) In the absence of r, i²R + i ε = 53
ε = \(\frac{53-\mathrm{i}^{2} \mathrm{R}}{\mathrm{i}}\)

(c) Since the current is directed from left to right, terminal A is positive.