Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 1 Probability Ex 1.1 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 1 Probability Ex 1.1
Question 1.
State the sample space for the following random experiments:
(1) A balanced coin is thrown three times.
Answer:
Total number of primary outcomes of
the random experiment of throwing a balanced coin thrice is n = 23 = 8.
- Head (H) obtained in all three trials, i.e., outcome HHH is obtained.
- Head (H) obtained in first two trials and Tail (T) obtained, in third trial, i.e., outcome HHT is obtained.
- Head (H) obtained in first trial, Tail (T) obtained in second trial and Head (H) obtained in third trial, i.e., outcome HTH is obtained.
- Tail (T) obtained in first trial and Head (H) obtained in rest of the two trials, i.e., outcome THH is obtained.
- Head (H) obtained in first trial and Tail (T) obtained in rest of the two trials, i.e., outcome HTT is obtained.
- Tail (T) obtained in first trial, Head (H) obtained in second trial and Tail (T) obtained in third trial, i.e., outcome THT is obtained.
- Tail (T) obtained in first two trials and Head (H) obtained in third trial, i.e., outcome TTH is obtained.
- Tail (T) obtained in all three trials, i.e., outcome TTT is obtained.
Hence, the sample space for the random experiment of throwing a balanced coin is expressed as follows:
U = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

(2) A balanced die with six sides and a balanced coin are tossed together.
Answer:
The sample space for the random experiment of tossing together a balance die and a balanced coin is expressed as follows :
U = {(1, H), (2, H), (3, H), (4, H), (5, H), (6, H), (1, T), (2, T), (3, T), (4, T), (5,T), (6, T)}
Where, in each bracket the first term is the number on die and second term is the outcome on the coin.
(3) Two persons are to be selected from five persons a, b, c, d, e.
Answer:
Total number of ways of selecting two persons from 5 persons
= 5C2 = \(\frac{5 \times 4}{2 \times 1}\) = 10
The sample space for the random experiment of selecting two persons from five persons a, b, c, d, e is expressed as follows:
U = {(a, b), (a, c), (a, d), (a, e), (b, c), (b, d), (b, e), (c, d), (c, e), (d, e)}
Question 2.
Write the sample space for the marks (in integers) scored by a student appearing for an examination of 100 marks and state the number of sample points in it.
Answer:
A student can get 0 mark or any number of marks in the close interval [1, 100].
So, the sample space for the marks scored by a student appearing for an examination of 100 marks is expressed as follows :
U = {0, 1, 2, 3, ……………, 100}
The number of sample points in the sample space U = 101.
Question 3.
Write the sample space for randomly selecting one minister and one deputy minister from four persons.
Answer:
Suppose, four persons are denoted by a, b, c and d. Firstly, one minister can be selected in 4C1 ways than secondly one deputy minister can be selected in 3C1 ways.
∴ Total number of selections = 4C1 × 3C1
= 4 × 3
= 12
Hence, the sample space for randomly selecting one minister and one deputy minister from four persons is expressed as follows:
U = {(a, b), (a, c), (a, d), (b, a), (b, c), (b, d), (c, a), (c, b), (c, d), (d, a), (d, b), (d, c)}.
Where, in each bracket, first place indicates minister and second place indicates deputy minister.

Question 4.
A balanced coin in thrown in a random experiment till the first head is obtained. The experiment is terminated with a trial of first head. Write the sample space of this experiment and state whether it is finite or infinite.
Answer:
A balanced coin is thrown till the first head is obtained. The options of this random experiment are as follows :
- Head (H) is obtained in the first trial, i.e., outcome H is obtained.
- Tail (T) is obtained in the first trial and Head (H) is obtained in second trial, i.e., outcome TH is obtained.
- Tail (T) is obtained in first two trials and Head (H) is obtained in third trial, i.e., outcome TTH is obtained.
- Tail (T) is obtained in first three trials and Head (H) is obtained in fourth trial, i.e., outcome TTTH is obtained.
In this manner outcomes TTTTH, TTTTTH, … are obtained. Thus, the number of outcomes of this random experiment is indefinite.
Hence, the sample space of the random experiment of throwing a balanced coin till the first head is obtained, is expressed as follows:
U = (H, TH, TTH, TTTH, …}
The sample space of this experiment is infinite.
Question 5.
Write the sample space for the experiment of randomly selecting three numbers from the first five natural numbers.
Answer:
First five natural numbers are 1, 2, 3, 4, 5. The number of ways of selecting three numbers from these five numbers is 5C3 = \(\frac{5 \times 4 \times 3}{3 \times 2 \times 1}\) = 10.
Hence, the sample space for the experiment of randomly selecting three numbers from the first five natural numbers is expressed as follows:
U = {(1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 3, 4), (1, 3, 5), (1, 4, 5), (2, 3, 4), (2, 3, 5), (2, 4, 5), (3, 4, 5)}.

Question 6.
The sample space of a random experiment of selecting a number is U = {1, 2, 3,…, 20}. Write the sets showing the following events:
(1) The selected number is odd number.
(2) The selected number is divisible by 3.
(3) The selected number is divisible by 2 or 3.
Answer:
Here, U = {1, 2, 3, …….., 20}
(1) A = Event that the selected number is odd number.
∴ A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
(2) B = Event that the selected number is divisible by 3
∴ B = {3, 6, 9, 12, 15, 18}
(3) C = Event that the selected number is divisible by 2 or 3
∴ C = (2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20}
Question 7.
One family is selected from the families having two children. The sex (male or female) of the children from this family is noted. State the sample space of this experiment and write the sets showing the following events:
(1) Event A1 = One child is a female
(2) Event A2 = At least one child is a female
Answer:
Here, let B = child is male; G = child is female.
The sample space of selecting one family from the families having two children is expressed as follows:
U = {(B, B), (B, G), (G, B), (G, G)}
(1) Event A1 = One child is a female
= {(B, G), (G, B)}
(2) Event A2 = At least one child is a female
= {(B, G), (G, B), (G, G)}

Question 8.
Two six faced balanced dice are thrown simultaneously. State the sample space of this random experiment and hence write the sets showing the following events:
(1) Event A1 = The sum of numbers on the dice is 7.
(2) Event A1 = The sum of numbers on the dice is less than 4.
(3) Event A3 = The sum of numbers on the dice is divisible by 3.
(4) Event A4 = The sum of numbers on the dice is more than 12.
Answer:
Two six faced balanced dice are thrown simultaneously. Hence, the sample space of this experiment is expressed as follows:
U = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
OR
U= {(i, J); i, j = 1, 2, 3, 4, 5, 6}
(1) Event A1 = The sum of numbers on the dice is 7
= {(1, 6), (2, 5), (3, 4)’ (4, 3), (5, 2), (6, 1)}
(2) Event A2 = The sum of numbers on the dice is less than 4, i.e., 2 or 3
= {(1, 1), (1, 2), (2, 1)}
(3) Event A3 = The sum of numbers on the dice is divisible by 3
= {(1, 2), (1, 5), (2, 1), (2, 4), (3, 3), (3, 6), (4, 2), (4, 5), (5, 1), (5, 4), (6, 3), (6, 6)}
(4) Event A4 = The sum of numbers on the dice is more than 12 = { } OR Φ
Question 9.
Two numbers are selected at random from the first five natural numbers. The sum of two selected numbers is at least 6 is denoted by event A and the sum of two selected numbers is even is denoted by event B. Write the sets showing the following events and answer the given questions:
(1) ∪
Answer:
The total number of ways of selecting two numbers at random from the first five natural numbers 1, 2, 3, 4, 5 is
5C2 = \(\frac{5 \times 4}{2 \times 1}\) = 10
U = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}
(2) A
Answer:
Event A = The sum of two selected numbers is at least 6
= {(1, 5), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}
(3) B
Answer:
Event B = The sum of two selected numbers is even
= {(1, 3), (1, 5), (2, 4), (3, 5)}
(4) A ∪ B
Answer:
Event A ∪ B = The sum of two selected numbers is at least 6 or even.
= {(1, 3), (1, 5), (2. 4), (2, 5), (3, 4), (3, 5), (4, 5)}

(5) A ∩ B
Answer:
Event A ∩ B = The sum of two selected numbers is at least 6 and even.
= {(1, 5), (2, 4), (3, 5)}
(6) A
Answer:
Event A’ = The sum of two selected numbers is at the most 6.
= U – A
= {(1, 2), (1, 3), (1, 4), (2, 3)}
(7) A – B
Answer:
Event A – B = The sum of two selected numbers is at least 6 but not even.
= Event A occurs but event B does not occur.
= A – (A ∩ B) = A ∩ B’
= {(2, 5), (3, 4), (4, 5)}
(8) A’ ∩ B
Answer:
Event A’ ∩ B = The sum of two selected number is not at least 6 but even.
= Even A does not occur but event B occurs.
= B – (A ∩ B) = B – A
= {(1, 3)}
(9) Can it be said that the events A and B are mutually exclusive? Give reason.
Answer:
A ∩ B ≠ Φ. Hence, events A and B are not mutually exclusive events.
(10) State the number of sample points in the sample space of this random experiment.
Answer:
Number of sample points = 10
Question 10.
Three female employees and two male employees are working in an office. One employee is selected from the employees of this office for training. The event that the employee selected for the training is a female is denoted by A and the event that this employee is a male is denoted by B. Find the sets showing the following events and answer the given questions:
(1) U
Answer:
Let three female employees be a, b, c and two male employees be x, y.
So, the sample space of selecting one employee is expressed as follows :
U = {a, b, c, x, y}
(2) A
Answer:
Event A = The employee selected for training is a female.
= {a, b, c}
(3) B
Answer:
Event B = The employee selected for training is a male.
= {x, y}
(4) A ∪ B
Answer:
Event A ∪ B = The employee selected for training is a female or male.
= {a, b, c, x, y} = U

(5) A ∩ B
Answer:
Event A ∩ B = The employee selected for training is a female and male.
= { } = Φ
(6) A’ ∩ B
Answer:
Event A’ ∩ B = The employee selected for training is a male but not a female.
= B – (A ∩ B)
= B – A = B = {x, y}
(7) Can it be said that the events A and B are mutually exclusive? Give reason.
Answer:
A ∩ B = Φ. Hence, events A and B are mutually exclusive events.
(8) Can it be said that the events A and B are exhaustive? Give reason.
Answer:
A ∪ B = U. Hence, events A and B are exhaustive events.
Question 11.
One card is randomly drawn from a pack of 52 cards. If drawing a spade card is denoted by event A and drawing a card from ace to ten (non-face card) is denoted by B then write the sets showing the following events:
(1) U
(2 ) A
(3 ) B
(4) A ∪ B
(5) A ∩ B
(6) B’
Answer:
A pack of 52 cards consists of 13 spade cards, 13 club cards, 13 heart cards and 13 diamond cards.
Let, S = Spade card,
C = Club card,
H = Heart card,
D = Diamond card,
J = Jack card,
Q = Queen card,
K = King card,
A = Ace card
Non-face card: Spade: S2, S3, S4, …, S10
Club: C2, C3, C4, …, C10
Heart: H2, H3, H4, …, H10
Diamond: D2, D3, D4, …, D10
Total number of ways of drawing a card randomly from a pack of 52 cards is 52C2 = 52

(1) U: The sample space of drawing a card randomly from a pack of 52 cards is expressed as follows:
u = {SA, S2, S3, S4, …….. S10, SJ, SQ, SK
CA, C2, C3, C4, …….. C10, CJ, CQ, CK
HA, H2, H3, H4, …….. H10, HJ, HQ, HK
DA, D2, D3, D4, …….. D10, DJ, DQ, DK}
(2) Event A = Drawing a spade card
SA, S2, S3, S4, …….. S10, SJ, SQ, SK
(3) Event B = Drawing a card from ace to ten
= {SA, S2, S3, …….. S10, CA, C2, C3, …….. C10, HA, H2, H3, …….. H10, DA, D2, D3, …….. D10,}
(4) Event A ∪ B = Drawing a spade card or a card from ace to ten
= {SA, S2, S3, S4, …….. S10, SJ, SQ, SK, CA, C2, C3, …….. C10, HA, H2, H3, …….. H10, DA, D2, D3, …….. D10}
(5 ) Event A ∩ B = Drawing a spade card and from ace to ten
= {SA, S2, S3, …….. S10}
(6) Event B’ = Drawing a face card (or not from ace to ten)
= {SJ, SQ, SK, CJ, CQ, CK, HJ, HQ, HK, DJ, DQ, DK}
Question 12.
The events A1 and A2 of a random experiment are as follows. Find the sets showing the union event A1 ∪ A2 and intersection event A1 ∩ A2.
A1 = {x|0 < x < 5}
A2 = {x|- 1 < x < 3, x is an integer}
Answer:
A1 = {x|0 < x < 5} = {1, 2, 3, 4}
A2 = {x| – 1 < x < 3, x is an integer} = {0, 1, 2}
Union event A1 ∪ A2:
A1 ∪ A2 = {1, 2, 3, 4} ∪ {0, 1, 2}
= {0, 1, 2, 3, 4} = {x|0 ≤ x < 5}
Intersection event A1 ∩ A2:
A1 ∩ A2 = {1, 2, 3, 4} ∩ {0, 1, 2}
= {1, 2}
= {x|x = 1, 2}
Question 13.
The events A1 and A2 of a random experiment are as follows. Find the sets showing the union event A1 ∪ A2 and intersection event A1 ∩ A2.
A1 = {x|2^x<6, x e N}
A2 = {x|3 < x < 9, x e N}
Answer:
A1 = {x|2 ≤ x < 6, x ∈ N}
∴ A1 = {2, 3, 4, 5}
A2 = {x|3 < x < 9, x ∈ N}
∴ A2 = {4, 5, 6, 7, 8}
Union event A1 ∪ A2:
A1 ∪ A2 = {x|2 ≤ x < 6} ∪ {x|3 < x < 9}
= {2, 3, 4, 5} ∪ {4, 5, 6, 7, 8}
= {2, 3, 4, 5, 6, 7, 8}
= {x|2 ≤ x ≤ 8, x ∈ N}
Intersection event A1 ∩ A2j:
A1 ∩ A2 = {x|2 ≤ x < 6} ∩ {x|3 < x < 9}
= {2, 3, 4, 5} ∩ {4, 5, 6, 7, 8}
= {4, 5}
= {x|x = 4, 5}

Question 14.
The sample space U of a random experiment and its event A are defined as follows. Find the complementary event A’ of A.
U = {x|x = 0, 1, 2, ………….. 10}
A = {x|x = 2, 4, 6}
Answer:
U = {x|x = 0, 1, 2, …, 10}
∴ U = {0, 1, 2, …, 10}
A = {x|x = 2, 4, 6}
∴ A = {2, 4, 6}
Complementary event A’:
A’ = {0, 1, 3, 5, 7, 8, 9, 10}
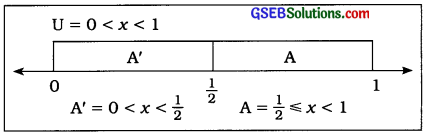
Question 15.
The sample space U of a random experiment and Its event A are defined as follows. Find the complementary event A’ of A.
U = {x|0 < x < 1}, A = {x|\(\frac{1}{2}\) ≤ x < 1}
Answer:
U = {x|0 < x < 1}
∴ U = \(\left\{\ldots, \frac{1}{10}, \frac{1}{8}, \frac{1}{4}, \frac{1}{2}, \frac{3}{4}, \ldots, \frac{9}{10}, \frac{99}{100}, \ldots\right\}\)
A = {x|\(\frac{1}{2}\) ≤ x < 1}
∴ A = \(\left\{\frac{1}{2}, \frac{3}{4}, \ldots, \frac{9}{10}, \frac{99}{100}, \ldots\right\}\)
Complementary event A’ :
A’ = \(\left\{\ldots \frac{1}{10}, \frac{1}{8}, \frac{1}{4}, \ldots\right\}\) = {x|0 < x < \(\frac{1}{2}\)}
The complementary event A’ can be well explained by the following diagram: