Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 2 Random Variable and Discrete Probability Distribution Ex 2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 2 Random Variable and Discrete Probability Distribution Ex 2
Section A
Answer the following questions by selecting a correct option from the given options:
Question 1.
Which variable of the following will be an illustration of discrete variable ?
(a) Height of a student
(b) Weight of a student
(c) Blood Pressure of a student
(d) Birth year of a student
Answer:
(d) Birth year of a student

Question 2.
Which variable of the following will be an illustration of continuous variable ?
(a) Number of accidents occurring at any place
(b) Number of rainy days during a year
(c) Maximum temperature during a day
(d) Number of children in a family
Answer:
(c) Maximum temperature during a day
Question 3.
A random variable X assume the values – 1, 0 and 1 with respective probability \(\frac{1}{5}\), k and \(\frac{1}{3}\), where 0 < k < 1 and X does not assume any value other than these values. What will be the value of E (X) ?
(a) \(\frac{2}{5}\)
(b) \(\frac{3}{5}\)
(c) \(\frac{2}{15}\)
(d) \(\frac{3}{15}\)
Answer:
(c) \(\frac{2}{15}\)
Question 4.
A random variable X assumes the values – 2, 0 and 2 only with respective probabilities \(\frac{1}{5}\), \(\frac{3}{5}\) and k. If 0 < k < 1, what will be the value of k?
(a) \(\frac{1}{5}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{2}{5}\)
(d) \(\frac{3}{5}\)
Answer:
(a) \(\frac{1}{5}\)
Question 5.
Mean and variance of a discrete probability distribution are 3 and 7 respectively. What will be E (X2) for this distribution ?
(a) 10
(b) 4
(c) 40
(d) 16
Answer:
(d) 16

Question 6.
For the probability distribution of a discrete random variable, E (X) 5 and E (X2) = 35. What will be the variance of this distribution ?
(a) 40
(b) 30
(c) 20
(d) 10
Answer:
(d) 10
Question 7.
For a positively skewed binomial distribution with n = 10, which of the following values might be the value of mean?
(a) 5
(b) 3
(c) 9
(d) 7
Answer:
(b) 3
Question 8.
For which value of x, the value of p (x) of binomial distribution with parameters n = 4 and p = \(\frac{1}{2}\) becomes maximum ?
(a) 0
(b) 2
(c) 3
(d) 4
Answer:
(b) 2
Question 9.
The binomial distribution has mean 5 and variance \(\frac{10}{7}\). What will be the type of this distribution ?
(a) Positively skewed
(b) Negatively skewed
(c) Symmetric
(d) Nothing can be said about the distribution
Answer:
(b) Negatively skewed

Question 10.
Which of the following is the formula of probability of an event of not getting a success in the binomial distribution with parameters n and p?
(a) nC0pnq0
(b) nC0p0qn
(c) nC0pqn
(d) nC0pnq
Answer:
(b) nC0p0qn
Section B
Answer the following questions in one sentence:
Question 1.
Define discrete random variable.
Answer:
A random variable X, which is capable of assuming all the values, in set of real numbers or its subsets, is called a discrete random variable. Examples of a discrete random variable are: number of children per family, getting number of heads when a coin is tossed three times.
Question 2.
Define continuous random variable.
Answer:
If a random variable X is an element of R or its subset, whose interval is (a, b), where a
Question 3.
Define discrete probability distribution.
Answer:
Suppose, probability of a discrete random variable X is p[X = xi] = p(xi). If for i = 1, 2, 3, ………, n; p (xi) > 0 and

then set of real values {p (x1), p(x2), ……, p (xn)} is called probability distribution of a discrete random variable X. In tabular form it is written as under:

Here, 0 < p (xi) < 1 and i = 1, 2, 3, …, n

Question 4.
State the formula to find mean of discrete variable.
Answer:
The formula to find mean of discrete variable is as follows :
µ = E(X) = Σ x ∙ p(x)
Question 5.
State the formula to find variance of discrete variable.
Answer:
The formula to find the variance of discrete variable is as follows :
σ2 = V(X) = E(X2) – [E(X)]2
= Σx2p (x) – [Σx ∙ p(x)]2
Question 6.
Mean of a symmetrical binomial distribution is 7. Find the value of its parameter n.
Answer:
Here, it is given that binomial distribution is symmetrical.
∴ p = q = \(\frac{1}{2}\)
Mean = np = 7 (Putting p = \(\frac{1}{2}\))
∴ n × \(\frac{1}{2}\) = 7
∴ n = 14
Hence, the value of parameter n obtained is 14.
Question 7.
The parameters of a binomial distribution are 10 and Calculate its variance.
Answer:
n = 10, p = \(\frac{2}{5}\)
∴ q = 1 – p = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
Variance = npq
= 10 × \(\frac{2}{5}\) × \(\frac{3}{5}\) = \(\frac{12}{5}\)
Hence, the variance obtained is \(\frac{12}{5}\).

Question 8.
State the relation between the probability of success and failure in Bernoulli trials.
Answer:
The relation between the probability of success and failure in Bernoulli trials is p + q = 1.
Question 9.
State the relation between mean and variance of binomial distribution.
Answer:
The relation between mean and variance s of binomial distribution is that the value of mean is always greater than variance, i.e., np > npq.
Question 10.
The probability of failure in a binomial distribution is 0.6 and the number of trials in it is 5. Find the probability of success.
Answer:
The probability of failure q = 0.6, n = 5
S The probability of success p = 1 – q
= 1 – 0.6
= 0.4

Section C
Answer the following questions as required:
Question 1.
The probability distribution of a random variable X is as follows:
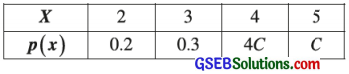
Determine the value of constant C.
Answer:
By condition of probability distribution, we must have
Σp(x) = 1
∴ p (2) + p (3) + p (4) + p (5) = 1
∴ 0.2 + 0.3 + 4C + C = 1
∴ 0.5 + 5 C = 1
∴ 5C = 1 – 0.5 = 0.5
∴ C = \(\frac{0.5}{5}\) = 0.1
Hence, the value of constant C obtained is 0.1.
Question 2.
Calculate mean of the discrete probability distribution
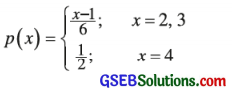
Answer:
Here, p (x) = \(\frac{x-1}{6}\) is given.
Putting, x = 2, 3
p(2) = \(\frac{2-1}{6}\) = \(\frac{1}{6}\)
P(3) = \(\frac{3-1}{6}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
and P(4) = \(\frac{1}{2}\)
So, the probability distribution of X is obtained as follows:

Mean of the distribution:
µ = Σx ∙ p(x)
= \(2\left(\frac{1}{6}\right)+3\left(\frac{1}{3}\right)+4\left(\frac{1}{2}\right)\)
= \(\frac{2}{6}\) + 1 + 2
= \(\frac{2+6+12}{6}\) = \(\frac{20}{6}\) = \(\frac{10}{3}\)
Hence, the mean of the distribution obtained is \(\frac{10}{3}\).

Question 3.
The probability distribution of a random variable is as follows:
p(x) = \(\frac{x+3}{10}\); x = – 2, 1, 2
Hence, calculate E (X2).
Answer:
Here, p (x) = \(\frac{x+3}{10}\) is given.
Putting x = – 2, 1, 2
P(- 2) = \(\frac{-2+3}{10}\) = \(\frac{1}{10}\)
P(1) = \(\frac{1+3}{10}\) = \(\frac{4}{10}\)
P(2) = \(\frac{2+3}{10}\) = \(\frac{5}{10}\)
To calculate E(X2), the following table is prepared:
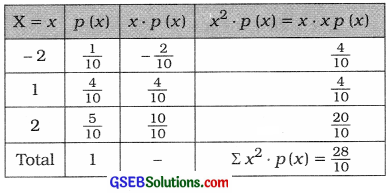
E(X2) = Σx2 ∙ p(x) = \(\frac{28}{10}\) = 2.8
Hence, E(x2) obtained is 2.8.
Question 4.
If n = 4 for a symmetrical binomial distribution, then find p (4).
Answer:
Here, n = 4 and a symmetrical binomial distribution is given.
∴ P = q = \(\frac{1}{2}\)
X is a binomial variable.
∴ p(X = x) = P(x) = nCxPxqn-x
Putting, n = 4, p = \(\frac{1}{2}\). q = \(\frac{1}{2}\)
p(x) = 4Cx \(\left(\frac{1}{2}\right)^{x}\left(\frac{1}{2}\right)^{4-x}\)
= 4Cx \(\left(\frac{1}{2}\right)^{4}\)
= \(\frac{{ }^{4} \mathrm{C}_{x}}{{ }^{16}}\)
∴ P(4) = \(\frac{{ }^{4} \mathrm{C}_{4}}{16}\) = \(\frac{1}{16}\)
Hence. p(4) obtained is \(\frac{1}{16}\).

Question 5.
Define Bernoulli trials.
Answer:
Suppose, a dichotomous experiment with only two outcomes – Success (S) and Failure (F) – is repeated n times under identical conditions and in each trial probability of success (S) p (0 < p < 1) is constant, then all such trials are called Bernoulli trials.
Question 6.
For a binomial distribution, if probability of success is double the probability of failure and n = 4, then find variance of the distribution.
Answer:
Probability of success = p and
Probability of failure = q
Probability of success Is twice the probability of failure,
∴ p = 2q
Now, putting p = 2q in p + q = 1,
2p + q = 1
∴ 3q = 1
∴ q = \(\frac{1}{3}\)
∴ p = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
Variance of distribution:
Putting. n = 4, p = \(\frac{2}{3}\) and q = \(\frac{1}{3}\) in npq
npq = 4 × \(\frac{2}{3}\) × \(\frac{1}{3}\) = \(\frac{8}{9}\)
Hence, the variance of the distribution obtained is \(\frac{8}{9}\).

Question 7.
Find the standard deviation of the binomial distribution having n = 8 and probability of failure
Answer:
n = 8, q = \(\frac{2}{3}\)
∴ p = 1 – q = 1 – \(\frac{2}{3}\) = \(\frac{1}{3}\)
Standard deviation of the binomial distribution:
√npq = \(\sqrt{8 \times \frac{1}{3} \times \frac{2}{3}}\) = \(\sqrt{\frac{16}{9}}\) = \(\frac{4}{3}\)
Hence, the standard deviation of the binomial distribution obtained is \(\frac{4}{3}\).
Question 8.
Find parameters of the binomial distribution where mean = 4 and variance = 2.
Answer:
Here, mean np = 4 and variance npq = 2 are given.
Now, q = \(\frac{n p q}{n p}\)
∴ q = \(\frac{2}{4}\) = \(\frac{1}{2}\)
∴ p = 1 – q = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Putting, P = \(\frac{1}{2}\) in np
∴ n × \(\frac{1}{2}\) = 4
∴ n = 8
Hence, the parameters of binomial distribution obtained are n = 8 and p = \(\frac{1}{2}\) respectively.
Question 9.
For a binomial distribution with n = 10 and q – p = 0.6, find mean of this distribution.
Answer:
n = 10, q – p = 0.6 are given,
q – p = 0.6
∴ 1 – p – p = 0.6
∴ 1 – 2p = 0.6
∴ 1 – 0.6 = 2p
∴ 0.4 = 2p
∴ p = \(\frac{0.4}{2}\) = 0.2
Mean of the distribution np = 10 × 0.2 = 2
Hence, mean of the distribution obtained is 2.

Question 10.
For a binomial distribution, standard deviation is 0.8 and probability of failure is find the mean of this distribution.
Answer:
Here, standard deviation of binomial distribution = √npq
√npq = 0.8
∴ npq = 0.64
Probability7 of failure q = \(\frac{2}{3}\)
Mean of the distribution:
Putting, q = \(\frac{2}{3}\) in npq = 0.64
np × \(\frac{2}{3}\) = 0.64
∴ np = \(\frac{0.64 \times 3}{2}\) = 0 96
Hence, the mean of the distribution obtained is 0.96.
Section D
Answer the following questions as required:
Question 1.
The probability distribution of a random variable X is as follows:

Find the value of constant k and the probability of the event that variable X assumes even numbers.
Answer:
The probability distribution of a random variation is given as follows:
p(x) = k(x – 1); x = 2, 3
∴ p(2) = K(2 – 1) = k
p (3) = k( 3 – 1) = 2k
p (x) = k; x = 4
∴ p(4) = k
p(x) = k(6 – x) = k
∴ p(5) = k(6 – 5) = k
By condition of probability distribution, we must have
Σp(x) = 1
∴ p (2) + p (3) + p (4) + p (5) = 1
∴ k + 2k + k + k = 1
∴ 5k = 1
∴ k = \(\frac{1}{5}\)
Probability that variable X assumes even numbers :
P[X = 2, 4]
= p(2) + p(4)
= k + k = 2k (Putting k = \(\frac{1}{5}\))
p(2) + p(4) = 2 × \(\frac{1}{5}\) = \(\frac{2}{5}\)
Hence, the probability that the variable X assumes even number obtained is \(\frac{2}{5}\).

Question 2.
The probability distribution of a random variable X is as follows:
p(x) = C(x2 + x), x = – 2, 1, 2
Find the value of C and show that p (2) = 3p (- 2).
Answer:
Here, p(x) = C(x2 + x),
Putting, x = – 2, 1, 2
p (- 2) = C[(- 2)2 + (-2)] = C(4 – 2) = 2C
p (1) = C[(1)2 + (1)] = 2C
p(2) = C[(2)2 + (2)] = 6C
By condition of probability distribution, we must have
Σp (x) = 1
∴ p(- 2) + p(1) + p(2) = 1
∴ 2C + 2C + 6C = 1
∴ 10 C = 1
∴ C = \(\frac{1}{10}\)
Now, putting C = \(\frac{1}{10}\) in p (2) = 6C
p(2) = 6 × \(\frac{1}{10}\) = \(\frac{3}{5}\)
Putting C = \(\frac{1}{10}\) in 3p(-2) = 2C
∴ 3p(- 2) = 3 × 2 × \(\frac{1}{10}\) = \(\frac{3}{5}\)
Hence, it is proved that p (2) = 3p(- 2) = \(\frac{3}{5}\).
Question 3.
The distribution of a random variable
X is p(x) = k ∙ 5Px; x = 0, 1, 2, 3, 4, 5
Find constant k and mean of this distribution.
Answer:
p(x) = k ∙ 5Px is given.
Putting, x = 0, 1, 2, 3, 4, 5
p(0) = k ∙ 5P0 = k\(\left(\frac{5 !}{5 !}\right)\) = k
p(1) = k ∙ 5P1 = k\(\left(\frac{5 !}{4 !}\right)\) = 5k
p(2) = k ∙ 5P2 = k\(\left(\frac{5 !}{3 !}\right)\) = 20k
P(3) = k ∙ 5P3 = k\(\left(\frac{5 !}{2 !}\right)\) = 60k
p(4) = k ∙ 5P4 = k\(\left(\frac{5 !}{1 !}\right)\) = 120k
p(5) = k ∙ 5P5 = k\(\left(\frac{5 !}{0 !}\right)\) = 120k
Now, by condition of probability distribution, we must have
Σ p(x) = 1
∴ p (0) + p(1) + p (2) + p (3) + p (4) + p (5) = 1
∴ k + 5k + 20k + 60k + 120k + 120k = 1
∴ 326k = 1
∴ k = \(\frac{1}{326}\).
Now, putting k = \(\frac{1}{326}\)
P(0) = k = \(\frac{1}{326}\)
P(1) = 5k = \(\frac{5}{326}\)
P(2) = 20k = \(\frac{20}{326}\)
P(3) = 60k = \(\frac{60}{326}\)
P(4) = 120k = \(\frac{120}{326}\)
P(5) = 120k = \(\frac{120}{326}\)
Calculation of mean:
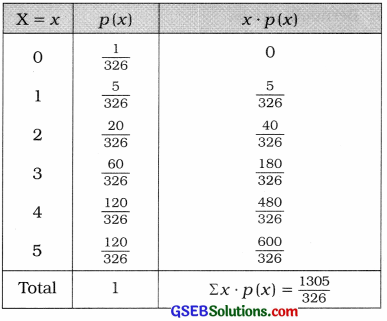
µ = Σx ∙ p(x) = \(\frac{1305}{326}\)
Hence, the mean of the distribution obtained is \(\frac{1305}{326}\).

Question 4.
What is discrete probability distribution ? State its properties.
Answer:
Suppose, probability of a discrete random variable. X is p[X = xi] = p(xi), where i = 1, 2, 3, ……, n, p(xi) > 0 and
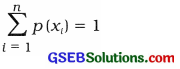
then set of real values {p(x1), p(x2), ……… p(xn)} is called probability distribution of a discrete random variable X. In tabular form it is written as follows:

Properties of discrete probability distribution:
- For each value x of X. p(x) > 0.
- Σ(x) = 1
Question 5.
State properties of binomial distribution.
Answer:
Properties of binomial distribution are as follows:
- It is a probability distribution of discrete random variable.
- The parameters of this distribution are n and p.
- The mean of the distribution is np, which shows the average number of successes in n Bernoulli trials.
- The variance of the distribution is npq and hence its standard deviation is √npq.
- In this distribution the value of its variance is always less than its mean. i.e..
npq < np and \(\frac{\text { Variance }}{\text { Mean }}\) = q. - If for any value of n. p = \(\frac{1}{2}\), it is symmetric distribution.
- If for any value of n, p < \(\frac{1}{2}\). the skewness of the distribution is positive. (8 ) If for any value of n, p > \(\frac{1}{2}\), the skewness of the distribution is negative.

Question 6.
In a game of hitting a target, the probability that Ramesh will fail in hitting the target is \(\frac{2}{5}\). If he is given 3 trials to hit the target, find the probability of the event that he hits the target successfully in 2 trials. State mean of this distribution.
Answer:
Here, n = 3
X = Number of trials In which the target Is successfully hit = 2.
p = Probability of hitting the target successfully
= 1 – (probabIlity of fail in hitting the target)
= 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
∴ q = 1 – p = \(\frac{2}{5}\)
X is binomial random variable.
∴ P(X = x) = p(x) = nCxpxqn-x
Putting, n = 3, x = 2, p = \(\frac{3}{5}\)
q = 1 – p = 1 – \(\frac{3}{5}\) = \(\frac{2}{5}\)

Hence. the probability of hitting the target successfully obtained is \(\frac{54}{125}\).
Mean of the distribution:
np = 3 x \(\frac{3}{5}\) = \(\frac{9}{5}\)
Question 7.
A person is asked to select a number from positive integers 1 to 7. If the number selected by him is odd then he is entitled to get the prize. If he is asked to take 5 trials then find the probability of the event that he will be entitled to get a prize in only one trial.
Answer:
Numbers are: 1, 2, 3, 4, 5, 6, 7, of which odd numbers are 1, 3, 5, 7 = 4.
∴ Probability of selecting odd number = \(\frac{4}{7}\)
Now, n = Number of trials = 5
X = Number of trials which is entitled to get the prize = 1
p = Probability of getting prize = \(\frac{4}{7}\)
∴ q = 1 – p = 1 – \(\frac{4}{7}\) = \(\frac{3}{7}\)
Putting, n = 5, x = 1, P = \(\frac{4}{7}\), q = \(\frac{3}{7}\) in
P(X = x) = p(x) = nCxpxqn-x
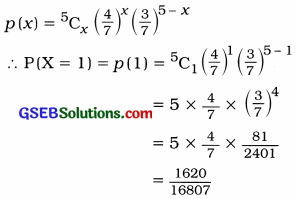
Hence, the probability that a person will be entitled to get a prize obtained is \(\frac{1620}{16807}\).

Question 8.
The mean and variance of the binomial distribution are 2 and \(\frac{6}{5}\) respectively. Find p (1) and p (2) for this binomial distribution.
Answer:
Here, np = 2 and npq = \(\frac{6}{5}\)

Question 9.
10 % apples are rotten in a box of apples. Find the probability that half of the 6 apples selected from the box with replacement will be rotten and find the variance of the number of rotten apples.
Answer:
In a box of apples 10 % apples are rotten.
∴ Probability that an apple is rotten p = \(\frac{10}{100}\) = \(\frac{1}{10}\)
∴ q = 1 – p = 1 – \(\frac{1}{10}\) = \(\frac{9}{10}\)
Now, n = 6, X = Number of rotten apples = 3
X is binomial random variable.
Putting, n = 6, x = 3, P = \(\frac{1}{10}\), q = \(\frac{9}{10}\) in
P(X = x) = p(x) = nCxpxqn-x
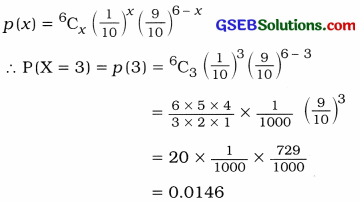
Variance:
Putting, n = 6, p = \(\frac{1}{10}\), q = \(\frac{9}{10}\)
npq = 6 × \(\frac{1}{10}\) × \(\frac{9}{10}\)
= 0.54

Section E
Solve the following:
Question 1.
The probability distribution of the monthly demand of laptop in a store is as follows:

Determine the expected monthly demand of laptop and find variance of the demand.
Answer:
The following table is prepared to determine the expected monthly demand and variance of demand of laptop:

Expected monthly demand of laptop:
E(x) = Σx ∙ p(x)
= 3.62 laptop
Variance of demand of laptop:
σ2 = V(X) = E(X2) – [E(X)]2
= Σx2 ∙ p(x) – [Σx ∙ p(x)]2
= 15.32 – (3.62)2
= 15.32 – 13.1044
= 2.2156
Question 2.
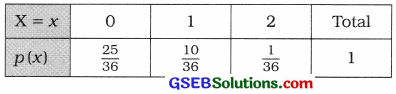
Two dice are thrown simultaneously once. Obtain the discrete probability distribution of the number of dice for which the number ‘6’ comes up.
Answer:
Two dice are thrown simultaneously.
∴ Total primary outcomes of U is n = 62 = 36
x is to get the number ‘6’ up.
The following table shows all possible outcomes and their probability.
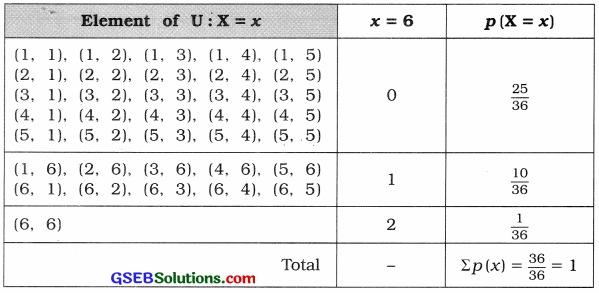
Hence, the probability distribution of getting x, that comes up is obtained as follows :

Question 3.
If the probability that any 50 year old person will die within a year is 0.01, find the probability that out of a group of 5 such persons
(i) none of them will die within a year
(ii) at least one of them will die within a year.
Answer:
Here, n = 5
p = Probability that any 50 year old person will die within a year = 0.01
∴ q = 1 – p = 1 – 0.01 = 0.99
X is binomial random variable.
∴ Putting, n = 5, p = 0.01, q = 0.99 in
P(X = x) = p(x) = nCxpxqn-x
P(X = x) = p(x) = 5Cx(0.01)x(0.99)n-x
(i) None of the 50 year old person will die within a year, i.e.,
X = 0
∴ P(X = 0) = p(0) = 5C0(0.01)0 (0.99)5-0
= 1 × 1 × (0.99)5
= 0.9510
(ii) At least one of them will die within a year, i.e., X ≥ 1
Now, P(X ≥ 1)
= p(1) + p (2) + p(3) + p( 4) + p (5)
= 1 – p(0)
= 1 – 0.9510
= 0.049
Question 4.
The probability that a student studying in 12th standard of science stream will get admission to engineering branch is 0.3. 5 students are selected from the students who studied in this stream. Find the probability of the event that the number of students admitted to engineering branch is more than the number of students who did not get admission to the engineering branch.
Answer:
Here, n = 5
p = Probability that a student will get admission to engineering branch = 0.3
∴ q = 1 – p = 1 – 0.3 = 0.7
X is binomial random variable.
∴ P(X = X) = p(x) = nCxpxqn-x
Putting, n = 5, p = 0.3, q = 0.7
P(X = x) = p(x) = 5Cx(0.3)x(0.7)5-x
X = At least three students will get admission in engineering branch
∴ X ≥ 3
Now, P(X ≥ 3) = p(3) + p(4) + p(5)
= [5C3(0.3)3 (0.7)5 – 3] + [5C4(0.3)4(0.7)5 – 4] + [5C5(0.3)5 (0.7)5 – 5]
= [10(0.027) (0.7)2] + [5(0.0081) (0.7)1] + [1 (0.00243) (0.7)0]
= [10 × 0.027 × 0.49] + [5(0.0081) (0.7)] + [1 × 0.00243 × 1]
= 0.1323 + 0.02835 + 0.00243
= 0.16308
= 0.1631

Question 5.
The probability that a bomb dropped from a plane over a bridge will hit the bridge is \(\frac{1}{5}\). Two bombs are enough to destroy the bridge. If 6 bombs are dropped on the bridge, find the probability that the bridge will be destroyed.
Answer:
Here, n = 6
p = Probability that a bomb dropped over a bridge = \(\frac{1}{5}\) = 0.2
X is binomial random variable.
∴ P(x = x) = p(x) = nCxpxqn-x
Putting, n = 6, p = \(\frac{1}{5}\) = 0.2, q = \(\frac{4}{5}\) = 0.8
P(X = x) = p(X) = 6Cx(0.2)x(0.8)6-x
Two bombs are enough to destroy the bridge. i.e., X ≥ 2
∴ P(X ≥ 2) = 1 – p[X ≤ 1]
= 1 – [p(0) + p(1)] ………… (1)
∴ p(0) = 6C0(0.2)0(0.8)6
= 1 × 1 × 0.2621 = 0.2621
∴ p(1) = 6C1(0.2)1(0.8)5
= 6 × 0.2 × 0.32768
= 0.3932
Putting the values of p(0) and p(1) in the result (1),
P[X ≥ 2] = 1 – [0.2621 + 0.3932]
= 1 – 0.6553
= 0.3447
Hence, the probability that the bridge will be destroyed obtained is 0.3447.
Question 6.
Normally, 40 % students fail in one examination. Find the probability that at least 4 students in a group of 6 students pass in this examination.
Answer:
40% student fail in the examination.
∴ Probability that a student fails = \(\frac{40}{100}\) = 0.4
p = Probability that student passes in the examination
= 1 – (Probability that a student fails)
= 1 – 0.4 = 0.6
q = 0.4, n = 6
X = At least 4 students pass in the examination.
∴ X = 4, 5, 6
X is binomial random variable.
∴ P(X = x) = p(x) = nCx px qn-x
Putting, n = 6, p = 0.6, q = 0.4
P(X = x) = p(x) = 6Cx (0.6)x (0.4)6-x
∴ p(4) = 6C4 (0.6)4 (0.4)6-4
= \(\left(\frac{6 \times 5 \times 4 !}{2 ! \times 4 !}\right)\) (0.1296) (0.4)2
= (15) (0.1296) (0.16) = 0.3110
∴ p(5) = 6C5 (0.6)5 (0.4)6-5
= \(\left(\frac{6 \times 5 !}{1 \times 5 !}\right)\) (0.0778) (0.4)
= (6) (0.0778) (0.4) = 0.1866
p(6) = 6C6 (0.6)6 (0.4)6-6
= (1) (0.0467) (1)
= 0.0467
Now, P(X ≥ 4) = p(4) + p(5) + p(6)
= 0.3110 + 0.1866 + 0.0467
= 0.5443
Hence, the probability that at least 4 students pass in the examination obtained is 0.5443.

Question 7.
There are 3 red and 4 white balls in a box. Four balls are selected at random with replacement from the box. Find the probability of the event of getting (i) 2 red balls and 2 white balls (ii) all four white balls among the selected balls using blnomia1 distribution.
Answer:
In a box there are total (3 red + 4 white =) 7 balls. 4 balls are selected at random with replacement.
∴ n = 4
The probability that a red ball selected is P = \(\frac{3}{7}\) and the probability that a red ball is not selected means a white ball selected is q = \(\frac{4}{7}\).
X is binomial random variable.
∴ P(X = x) = p(x) = nCx px qn-x
Putting, n = 4, p = \(\frac{3}{7}\), q = \(\frac{4}{7}\)
P(X = x) = p(x) = 4Cx \(\left(\frac{3}{7}\right)^{x}\left(\frac{4}{7}\right)^{4-x}\)
(i) Probability that 2 red balls and 2 white balls are selected:
Putting X = 2,
P(X = 2) = p(2) = 4C2 \(\left(\frac{3}{7}\right)^{2}\left(\frac{4}{7}\right)^{4-2}\)
= 6 \(\left(\frac{9}{49}\right)\left(\frac{4}{7}\right)^{2}\)
= 6 × \(\frac{9}{49}\) × \(\frac{16}{49}\)
= \(\frac{864}{2401}\)
= 0.3599
(ii) Probability that all 4 white balls are selected, i.e., none is red ball.
∴ X = 0
P(X = 0)=p(0) = 4C0 \(\left(\frac{3}{7}\right)^{0}\left(\frac{4}{7}\right)^{4-0}\)
= 1 × 1 × \(\left(\frac{4}{7}\right)^{4}\)
= 1 × 1 × \(\frac{256}{2401}\)
= 0.1066

Section F
Solve the following:
Question 1.
There are one dozen mangoes in a box of which 3 mangoes are rotten. 3 mangoes are randomly selected from the box without replacement. If X denotes the number of rotten mangoes in the selected mangoes, obtain the probability distribution of X and hence find expected value and variance of the rotten mangoes in the selected mangoes.
Answer:
In a box there are one dozen, i.e., 12 mangoes of which 3 mangoes are rotten.
3 mangoes are randomly selected from the box.
X = In selected 3 mangoes, the number of rotten mangoes.
∴ X = 0, 1, 2, 3
Now, P(X = 0) = \(\frac{{ }^{3} \mathrm{C}_{0} \times{ }^{9} \mathrm{C}_{3}}{{ }^{12} \mathrm{C}_{3}}\) = \(\frac{1 \times 84}{220}\) = \(\frac{84}{220}\)
P(X = 1) = \(\frac{{ }^{3} \mathrm{C}_{1} \times{ }^{9} \mathrm{C}_{2}}{{ }^{12} \mathrm{C}_{3}}\) = \(\frac{3 \times 36}{220}\) = \(\frac{108}{220}\)
P(X = 2) = \(\frac{{ }^{3} \mathrm{C}_{2} \times{ }^{9} \mathrm{C}_{1}}{{ }^{12} \mathrm{C}_{3}}\) = \(\frac{3 \times 9}{220}\) = \(\frac{27}{220}\)
P(X = 3) = \(\frac{{ }^{3} \mathrm{C}_{3} \times{ }^{9} \mathrm{C}_{0}}{{ }^{12} \mathrm{C}_{3}}\) = \(\frac{1 \times 1}{220}\) = \(\frac{1}{220}\)
The probability distribution of X is obtained as follows:

The following table is prepared to find the expected value and variance of rotten mangoes:
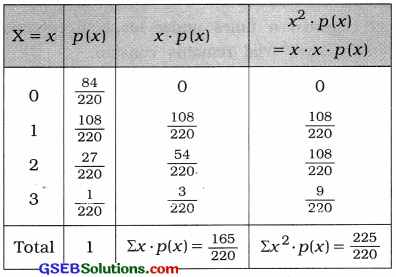
Expected value of rotten mangoes:
E(X) = Σx ∙ p(x)
= \(\frac{165}{220}\) mangoes
Variance of rotten mangoes :
σ2 = V(X) = E(X2) – [E (X)]2
= Σx2p(x) – [Σx p(x)]2
= \(\frac{225}{220}-\left(\frac{165}{220}\right)^{2}\)
= 1.0227 – (0.75)2
= 1.0227 – 0.5625
= 0.4602

Question 2.
It is known that 50 % of the students studying in the 10th standard have a habit of eating chocolate. To examine the information, 1024 investigators are appointed. Every investigator randomly selects 10 students from the population of such students and examines them for the habit of eating chocolate. Find the expected number of investigators who inform that less than 30 per cent of the students have a habit of eating chocolate.
Answer:
50 % of the students have a habit of eating chocolate.
∴ The probability that a student has habit of eating chocolate is p = \(\frac{50}{100}\) = \(\frac{1}{2}\).
∴ q = 1 – P = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Here, n = 10
X = From the selected 10 students less than 30% of students, i.e., \(\left(\frac{10 \times 30}{100}\right)\) = 3 students have a habit of eating chocolate.
= < 3
X is a binomial random variable.
∴ P(X = x) = p(x) = nCx px qn-x
Putting, n = 10, p = \(\frac{1}{2}\), q = \(\frac{1}{2}\) ,
P(X = x) = p(x) = 10Cx \(\left(\frac{1}{2}\right)^{x}\left(\frac{1}{2}\right)^{10-x}\)
= 10Cx \(\left(\frac{1}{2}\right)^{10}\)
= 10Cx \(\left(\frac{1}{2}\right)^{10}\)
= \(\frac{{ }^{10} \mathrm{C}_{x}}{1024}\)
Now, P(X < 3) =p(0) + p(1) + p(2)
= \(\frac{{ }^{10} \mathrm{C}_{0}}{1024}+\frac{{ }^{10} \mathrm{C}_{1}}{1024}+\frac{{ }^{10} \mathrm{C}_{2}}{1024}\)
= \(\frac{1}{1024}+\frac{10}{1024}+\frac{45}{1024}\)
= \(\frac{56}{1024}\)
Total number of investigators N = 1024
∴ The expected number of investigators who report that less than 30 % of students have a habit of eating chocolate is
= N × P(X < 3)
= 1024 × \(\frac{56}{1024}\) = 56