GSEB Solutions Class 12 Statistics Part 2 Chapter 5 Differentiation Ex 5

Gujarat Board Statistics Class 12 GSEB Solutions Part 2 Chapter 5 Differentiation Ex 5 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Statistics Part 2 Chapter 5 Differentiation Ex 5

Section A

Answer the following questions by selecting a correct option from the given options:

Question 1.
What is the formula for derivative of function f(x)?
(a)
(b)
(c)
(d)
Answer:
(c)

Question 2.
What is \(\frac{d y}{d x}\) if y = axⁿ, a is a constant?
(a) nx^{n – 1}
(b) an x^n-1
(c) 0
(d) anxⁿ⁺¹
Answer:
(b) an x^n-1

Question 3.
If y = ax + b, a and b are constants, then what will be
(a) a
(b) b
(c) a + b
(d) 0
Answer:
(a) a

Question 4.
What is the derivative of f(x) = \(\frac{4}{x^{2}}\)
(a) \(\frac{4}{2 x}\)
(b) – \(\frac{8}{x^{3}}\)
(c) \(\frac{8}{x^{3}}\)
(d) 0
Answer:
(b) – \(\frac{8}{x^{3}}\)

Question 5.
If u and v are two functions of x, then what is the formula of derivative of their product?
(a) \(u \cdot \frac{d u}{d x}+v \cdot \frac{d v}{d x}\)
(b) \(u \cdot \frac{d v}{d x}-v \cdot \frac{d u}{d x}\)
(c) \(\frac{d u}{d x} \times \frac{d v}{d x}\)
(d) \(u \cdot \frac{d v}{d x}+v \cdot \frac{d u}{d x}\)
Answer:
(d) \(u \cdot \frac{d v}{d x}+v \cdot \frac{d u}{d x}\)

Question 6.
If u and v are functions of x. then what is the formula of derivative of \(\frac{v}{u}\)?
(a) \(\frac{v \cdot \frac{d u}{d x}-u \cdot \frac{d v}{d x}}{v^{2}}\)
(b) \(\frac{v \cdot \frac{d u}{d x}+u \cdot \frac{d v}{d x}}{v^{2}}\)
(c) \(\frac{u \cdot \frac{d v}{d x}+v \cdot \frac{d u}{d x}}{u^{2}}\)
(d) \(\frac{u \cdot \frac{d v}{d x}-v \cdot \frac{d u}{d x}}{u^{2}}\)
Answer:
(d) \(\frac{u \cdot \frac{d v}{d x}-v \cdot \frac{d u}{d x}}{u^{2}}\)

Question 7.
If the function f(x) is increasing at x = a, then which is the correct option from the following?
(a) f ‘(a) < 0 (b) f ‘(a) > 0
(c) f ’(a) = 0
(d) f ”(a) > 0
Answer:
(b) f ‘(a) > 0

Question 8.
What are the necessary and sufficient conditions for a function to be minimum at x = a?
(a) f’(a) = 0, f’’(a) < 0 (b) f’(a) > 0, f”(a) > 0
(c) f’(a) = 0, f”(a) > 0
(d) f’(a) < 0, f’(a) > 0
Answer:
(c) f’(a) = 0, f”(a) > 0

Question 9.
What is the formula for elasticity of demand?
(a) – \(\frac{p}{x} \cdot \frac{d x}{d p}\)
(b) \(\frac{p}{x} \cdot \frac{d x}{d p}\)
(c) – \(\frac{x}{p} \cdot \frac{d p}{d x}\)
(d) \(\frac{p}{x} \cdot \frac{d p}{d x}\)
Answer:
(a) – \(\frac{p}{x} \cdot \frac{d x}{d p}\)

Question 10.
What are the conditions of revenue function R to be maximum ?
(a) \(\frac{d \mathrm{R}}{d x}\) = 0, \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) < 0 (b) \(\frac{d \mathrm{R}}{d x}\) = 0, \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) > 0
(c) \(\frac{d \mathrm{R}}{d x}\) > 0, \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) < 0 (d) \(\frac{d \mathrm{R}}{d x}\) > 0, \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) > 0
Answer:
(a) \(\frac{d \mathrm{R}}{d x}\) = 0, \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) < 0

Section B

Answer the following questions in one sentence:

Question 1.
Define differentiation.
Answer:
The process of obtaining derivative of a function is called differentiation.

Question 2.
Find f'(x) for the function f(x) = 50.
Answer:
For the function f(x) = 50, f'(x) = 0

Question 3.
Find \(\frac{d y}{d x}\) if y = aⁿ, a is constant.
Answer:
If y = aⁿ; a = constant, then \(\frac{d y}{d x}\) = 0.

Question 4.
State the rule for derivative for product of two functions of x.
Answer:
If u and v are differentiable functions of x and y = u ∙ v, then rule for derivative for product of two functions of x is as follows :
\(\frac{d y}{d x}\) = u ∙ \(\frac{d v}{d x}\) + v ∙ \(\frac{d u}{d x}\)

Question 5.
How will be the first order derivative of a function at x = a if function is decreasing at x = a ?
Answer:
If at x = a function is decreasing, then the first order derivative of a function at x = a is negative, i.e., f'(a) < 0.

Question 6.
How will be the second order derivative of a function at x = a if function is maximum at x = a ?
Answer:
If function is maximum at x = a, the second order derivative of a function at x = a will be negative, i.e., f ”(a) < 0.

Question 7.
What are the stationary points of a function ?
Answer:
The points where maximum or minimum value occur are known as stationary points of a function.

Question 8.
What is marginal revenue ?
Answer:
The change in revenue due to small change in demand is called marginal revenue.

Question 9.
Define marginal cost,
Answer:
The change in cost due to small change in production is called marginal cost.

Question 10.
State the formula of elasticity of demand.
Answer:
The formula of elasticity of demand is as follows:
Elasticity of demand = – \(\frac{\text { Percentage change in demand }}{\text { Percentage change in price }}\)
= – \(\frac{p}{x} \cdot \frac{d x}{d p}\)

Question 11.
Find f'(x) if f(x) = 7x² – 6x + 5.
Answer:
If f(x) = 7x² – 6x + 5, then
f(x) = 7 (2x) – 6(1) + 0
= 14x – 6

Question 12.
Find \(\frac{d y}{d x}\) if y = 6x³ + \(\frac{7}{2}\)x² + \(\frac{6}{5}\)x – 8.
Answer:
If y = 6x³ + \(\frac{7}{2}\)x² + \(\frac{6}{5}\)x – 8, then
\(\frac{d y}{d x}\) = 6(3x²) + \(\frac{7}{2}\)(2x) + \(\frac{6}{5}\)(1) – 0
= 18x² + 7x + \(\frac{6}{5}\)

Section C

Answer the following Questions as required:

Question 1.
Define derivative.
Answer:
Let f: A → R and a ∈ A, where A is an open interval of R. If h is made very small and exists, then this limit of a function f is called derivative at x = a. It is denoted by f ‘(a).

→ For any value of x of the domain of f,

→ If y = f(x), then f’(x) is denoted by \(\frac{d y}{d x}\)

Question 2.
State the division rule of derivative.
Answer:
u and v are differentiable functions of x,
If y = \(\frac{u}{v}\); v ≠ 0, then the division rule of derivative is as follows:

y = \(\frac{u}{v}\), then \(\frac{d y}{d x}\) = \(\frac{v \cdot \frac{d u}{d x}-u \cdot \frac{d v}{d x}}{v^{2}}\)

→ Thus, derivative of y

Question 3.
State necessary and sufficient conditions for a function to he maximum at x = a.
Answer:
Suppose, y = f(x).
The necessary and sufficient conditions for a function f (x) to be maximum at x = a are as follows :

• Necessary condition: f ‘ (a) = 0
• Sufficient condition: f “(a) < 0 (Negative)

Question 4.
Explain marginal cost and give its formula.
Answer:
If the cost of producing x units of an item is denoted by C. then C is a function of x.

• The change in C with respect to a small change in x is called marginal cost.
• Total cost C is a function of production x.
  So the derivative of C with respect to x is marginal cost.
• Thus, marginal cost = \(\frac{d \mathrm{C}}{d x}\)

Question 5.
Define elasticity of demand.
Answer:
The ratio of percentage change in demand and the percentage change in price is called elasticity of demand.

• Thus, Elasticity of demand
  = – \(\frac{\text { Percentage change in demand }}{\text { Percentage change in price }}\)
• The demand of an item x is a function of the price of an item p, i.e., x = f(p). So the elasticity of demand = – \(\frac{p}{x} \cdot \frac{d x}{d p}\).
• The relation between demand of an item and its price is inverse. Hence, negative sign is taken in the formula of elasticity of demand.

Question 6.
What are the conditions for profit function P to be maximum?
Answer:
The conditions for profit function P to be maximum are as follows:

• Necessary condition: \(\frac{d \mathrm{P}}{d x}\) = 0
• Sufficient condition: \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0 (Negative)

Question 7.
State the conditions for production cost function C to be minimum.
Answer:
The conditions for production cost function C to be minimum are as follows:

• Necessary condition: \(\frac{d \mathrm{C}}{d x}\) = 0
• Sufficient condition: = \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) > 0 (Positive)

Question 8.
Find f”(x) if f(x) = \(\sqrt[4]{x}\).
Answer:

Question 9.
Write the chain rule of differentiation.
Answer:
If y is a differentiable function of u and u is a differentiable function of x, then chain rule of differentiation is as follows:
\(\frac{d y}{d x}\) = \(\frac{d y}{d u}\) × \(\frac{d u}{d x}\)

Question 10.
Find f”(0) if f(x) = x⁴ – 4x³ + 3x² + x + 1.
Answer:
f(x) = x⁴ – 4x³ + 3x² + x + 1
∴ f'(x) = 4x³ – 12x² + 6x + 1
Now, f”(x) = \(\frac{d}{d x}\) [f'(x)]
= \(\frac{d}{d x}\) [4x³ – 12x² + 6x + 1]
= 12x² – 24x + 6

Putting, x = 0
f”(0) = 12(0) – 24(0) + 6 = 6
Hence, fix) = x⁴ – 4x³ + 3x² + x + 1 then f”(0) obtained is 6.

Question 11.
Find marginal revenue if revenue function is 90x – \(\frac{x^{2}}{2}\)
Answer:
R = 90x – \(\frac{x^{2}}{2}\)
Marginal revenue = \(\frac{d \mathrm{R}}{d x}\)
= \(\frac{d}{d x}\) [90x – \(\frac{x^{2}}{2}\)]
= 90(1) – \(\frac{2 x}{2}\)
= 90 – x

Question 12.
What is maximum value of a function?
Answer:
y = f(x) is a function. At x = a the value of function is maximum means the value of the function is maximum in a small interval around x = a.
→ Suppose, small interval around x = a is h.
→ If f(a) > f(a + h) and f(a) > f(a -h), then it can be said that at x = a, the maximum value of functionis obtained.

Question 13.
When can it be said that a function is decreasing at a point?
Answer:
Suppose, y = f (x) is a function and h is a very small positive number.

→ If at a point x = a. f(a + h) < f(a) and f(a) < f(a – h), then at x = a, function f(x) is called decreasing function. For such decreasing function f'(a) < 0.

Question 14.
Determine whether the function y = 12 + 4x – 7x² is increasing or decreasing at x = 2.
Answer:
y = 12 + 4x – 7x²
∴ \(\frac{d y}{d x}\) = 0 + 4(1) – 7(2x)
= 4 – 14x
At x = 2, \(\frac{d y}{d x}\) = 4 – 14 (2) = 4 – 28 = – 24
Here, at x = 2, \(\frac{d y}{d x}\) = – 24 < 0. Hence, the given function is decreasing function at x = 2.

Question 15.
Find the derivative of y = 4x² + 4x + 8. For which value of x will the derivative be zero ?
Answer:
y = 4x² + 4x + 8
∴ \(\frac{d y}{d x}\) = 4(2x) + 4(1) + 0
= 8x + 4
Now, \(\frac{d y}{d x}\) = 0
∴ 0 = 8x + 4
∴ – 8x = 4
∴ x = – \(\frac{4}{8}\) = – \(\frac{1}{2}\)
Hence, at x = – \(\frac{1}{2}\) the derivative will be zero.

Question 16.
f(x) = x³ + 5x² + 3x + 7, prove that f’(2) = 35.
Answer:
f(x) = x³ + 5x² + 3x + 7
∴ f’(x) = 3x² + 5(2x) + 3(1) + 0
= 3x² + 10x + 3
Putting, x = 2
f’(2) = 3(2)² + 10(2) + 3
= 3 × 4 + 20 + 3
= 12 + 20 + 3 = 35
Hence, it is proved that f’(2) = 35.

Question 17.
If f (x) = 3x² + 3, then for which value of x, f'(x) = f(x) ?
Answer:
f(x) = 3x² + 3
∴ f'(x) = 3(2x) + 0 = 6x
Now, f'(x) = f(x)
∴ 6x = 3x² + 3
∴ 3x² – 6x + 3 = 0
∴ x² – 2x + 1 = 0
∴ (x – 1)² = 0
∴ x – 1 = 0
∴ x = 1
Hence, for x = 1, f'(x) = f'(x)

Question 18.
Find \(\frac{d^{2} y}{d x^{2}}\) if y = 2x³ + 5x² – 3 + \(\frac{4}{x^{2}}\) – \(\frac{5}{x^{3}}\).
Answer:
y = 2x³ + 5x² – 3 + \(\frac{4}{x^{2}}\) – \(\frac{5}{x^{3}}\)
∴ y = 2x³ + 5x² – 3 + 4x^-2 – 5x^-3
∴ \(\frac{d y}{d x}\) = 2(3x²) + 5(2x) – 0 + 4(- 2)x^{– 2 – 1} – 5(- 3)x^{– 3 – 1}
= 6x² + 10x – 8x^{– 3} + 15x^{– 4}
Now, \(\frac{d^{2} y}{d x^{2}}\)
= \(\frac{d}{d x}\left[\frac{d y}{d x}\right]\)
= \(\frac{d}{d x}\) [6x² + 10x – 8x^{– 3} + 15x^{– 4}]
= 6(2x) + 10(1) – 8 (- 3) x^{– 3 – 1} + 15(- 4) x^{– 4 – 1}
= 12x + 10 + 24x^{– 4} – 60x^{– 5}
= 12x + 10 + \(\frac{24}{x^{4}}\) – \(\frac{60}{x^{5}}\)
Hence, \(\frac{d^{2} y}{d x^{2}}\) obtained is 12x + 10 + \(\frac{24}{x^{4}}\) – \(\frac{60}{x^{5}}\)

Question 19.
Find \(\frac{d^{2} y}{d x^{2}}\) if y = \(\sqrt{x}+\frac{1}{\sqrt{x}}\).
Answer:

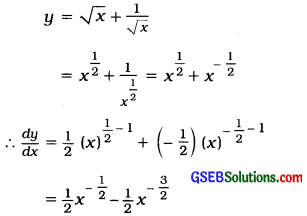
Question 20.
Obtain marginal cost if the production cost function is C = 0.0012x² – 0.18x + 25.
Answer:
C = 0.0012x² – 0.18x + 25
Now, marginal cost
= \(\frac{d \mathrm{C}}{d x}\)
= \(\frac{d}{d x}\) [0.0012x² – 0.18x + 25]
= 0.0012 (2x) – 0.18(1) + 0
= 0.0024x – 0.18
Hence, C = 0.0012x² – 0.18x + 25 then marginal cost obtained is 0.0024x – 0.18.

Section D

Answer the following questions as required:

Question 1.
Find derivative of y = ax + b (a and b are constants) using definition.
Answer:
Here, y = ax + b
∴ (y + h) = a (x + h) = ax + ah + b

Question 2.
Find derivative of f (x) = x¹⁰ using definition.
Answer:
Here, f(x) = x¹⁰
∴ f(x + h) = (x + h)¹⁰

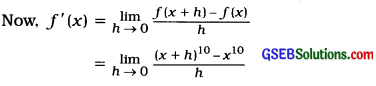
Take, x + h = t. When h → 0, t → x and h = t – x

Hence, f(x) = x¹⁰ then f ‘(x) = 10x⁹

Question 3.
Find derivative of \(\frac{2}{3+4 x}\) using definition.
Answer:

Question 4.
y = x³ – 3x² – 3x + 80. For which value of x, \(\frac{d y}{d x}\) = – 6
Answer:
y = x³ – 3x² – 3x + 80
∴ \(\frac{d y}{d x}\) = 3x² – 3(2x) – 3(1) + 0
= 3x² – 6x – 3
Hence, f(x) = x10 then /'(x) = 10×9
But \(\frac{d y}{d x}\) = – 6
∴ – 6 = 3x² – 6x – 3
∴ 3x² – 6x – 3 + 6 = 0
∴ 3x² – 6x + 3 = 0
∴ 3 (x² – 2x + 1) = 0
∴ x² – 2x + 1 = 0
∴ (x – 1)² = 0
∴ x – 1 = 0
∴ x = 1
Hence, when x = 1 \(\frac{d y}{d x}\) = – 6.

Question 5.
Find f ‘(2) if f(x) = \(\frac{4 x^{5}+3 x^{3}+2 x^{2}+24}{x^{2}}\)
Answer:
f(x) = \(\frac{4 x^{5}+3 x^{3}+2 x^{2}+24}{x^{2}}\)
= \(\frac{4 x^{5}}{x^{2}}+\frac{3 x^{3}}{x^{2}}+\frac{2 x^{2}}{x^{2}}+\frac{24}{x^{2}}\)
= 4x³ + 3x + 2 + 24x^{– 2}
∴ f’(x) = 4(3x²) + 3(1) + 0 + 24(- 2)x^{– 2 – 1}
= 12x² + 3 – 48x^{– 3}
= 12x² + 3 – \(\frac{48}{x^{3}}\)
Putting, x = 2
f’(2) = 12(2)² + 3 – \(\frac{48}{(2)^{3}}\)
= (12 × 4) + 3 – \(\frac{48}{8}\)
= 48 + 3 – 6
= 45
Hence, if f(x) = \(\frac{4 x^{5}+3 x^{3}+2 x^{2}+24}{x^{2}}\)
then f’(2) = 45.

Question 6.
Find the derivative of y = (3x² + 4x – 2) (3x + 2) with respect to x.
Answer:
y = (3x² + 4x – 2) (3x + 2)
Suppose, u = 3x² + 4x – 2
∴ \(\frac{d y}{d x}\) = 3 (2x) + 4(1) – 0
= 6x + 4
and v = 3x + 2
∴ \(\frac{d v}{d x}\) = 3(1) + 0 = 3
Now, y = u ∙ v
∴ \(\frac{d y}{d x}\) = u ∙ \(\frac{d v}{d x}\) + v ∙ \(\frac{d u}{d x}\)
= (3x² + 4x – 2) 3 + (3x + 2) (6x + 4)
= 9x² + 12x – 6 + 18x² + 12x + 12x + 8
= 27x² + 36x + 2
Hence, y = (3x² + 4x – 2) (3x + 2) then \(\frac{d y}{d x}\) = 27x² + 36x + 2.

Question 7.
Find \(\frac{d y}{d x}\) if y = \(\frac{a x+b}{b x+a}\) (a and b are constants).
Answer:

Question 8.
Find the derivative of y = 1 + \(\frac{1}{1+\frac{1}{x}}\) with respect to x.
Answer:

Question 9.
Find \(\frac{d y}{d x}\) if (2x + 3) (y + 2) = 15.
Answer:

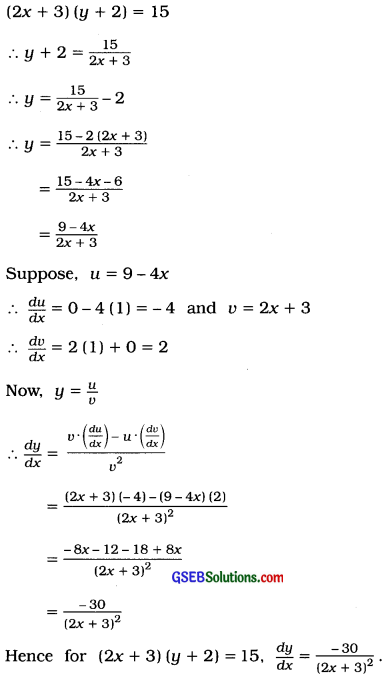
Question 10.
Find \(\frac{d y}{d x}\) if y = 5 + \(\frac{6}{7 x+8}\)
Answer:

Question 11.
Find f ‘(x) if f(x) = \(\sqrt{x^{2}+5}\)
Answer:

Question 12.
Find the derivative of \(\left(3 x^{3}-2 x^{2}+1\right)^{\frac{5}{2}}\) with respect to x.
Answer:

Question 13.
Find f'(x) if f(x) = (x² + 3x + 4)⁷.
Answer:
f(x) = (x² + 3x + 4)⁷
Taking, u = x² + 3x + 4
f(x) = u⁷
As per the chain rule,
f'(x) = \(\frac{d}{d u}\)(u⁷) × \(\frac{d}{d x}\)(x² + 3x + 4)
= 7u⁶ × (2x + 3)
Putting, u = x² + 3x + 4
f'(x) = 7(x² + 3x + 4)⁶ ∙ (2x + 3)
Hence, f(x) = (x² + 3x + 4)⁷ then
f'(x) = 7(x² + 3x + 4)⁶ ∙ (2x + 3).

Question 14.
If f(x) = 3x² + 4x + 5, then for which value of x, f ‘(x) = f “(x)?
Answer:
f(x) = 3x² + 4x + 5
∴ f ’(x) = 3(2x) + 4(1) + 0
= 6x + 4
Now f ”(x) = \(\frac{d}{d x}\) [f’(x)]
= \(\frac{d}{d x}\) [6x + 4]
= 6 + 0 = 6
But f ‘(x) = f “(x)
∴ 6x + 4 = 6
∴ 6x = 6 – 4
∴ 6x = 2
∴ x = \(\frac{2}{6}\) = \(\frac{1}{3}\)
Hence, for f(x) = 3x² + 4x + 5 when x = \(\frac{1}{3}\), f ‘(x) = f “(x).

Question 15.
Find marginal revenue if demand function is P = \(\frac{2500-x^{2}}{100}\).
Answer:

Question 16.
Determine whether the function y = 3x² – x + 7 is increasing or decreasing at x = 1 and x = 2.
Answer:
y = 3x² – x + 7
∴ \(\frac{d y}{d x}\) = 3(2x) – 10(1) + 0
= 6x – 10
At, x = 1 \(\frac{d y}{d x}\) = 6(1) – 10 = 6 – 10 = – 4 < 0. So, at x = 1 function is decreasing. At x = 2, \(\frac{d y}{d x}\) = 6(2) – 10 = 12 – 10 = 2 > 0.
So, at x = 2 function is increasing.

Question 17.
Determine whether the function y = 2x³ – 7x² – 11x + 5 is increasing or decreasing at x = \(\frac{1}{2}\) and x = 3.
Answer:
y = 2x³ – 7x² – 11x + 5
∴ \(\frac{d y}{d x}\) = 2(3x²) – 7(2x) – 11(1) + 0
= 6x² – 14x – 11
At x = \(\frac{1}{2}\), \(\frac{d y}{d x}\) = 6\(\left(\frac{1}{2}\right)^{2}\) – 14\(\left(\frac{1}{2}\right)\) – 11
= \(\frac{6}{4}\) – 7 – 11
= \(\frac{6}{4}\) – 18
= \(\frac{6 -72}{4}\)
= –\(\frac{66}{4}\), < 0
So, at x = \(\frac{1}{2}\) function is decreasing.
At x = 3, \(\frac{d y}{d x}\) = 6(3)² – 14(3) – 11
= (6 × 9) – 42 – 11
= 54 – 53 = 1 > 0
So, at x = 3 function is increasing.

Question 18.
Determine whether the function y = 3 + 2x – 7x² is increasing or decreasing at x = – 4 and x = 4.
Answer:
y = 3 + 2x – 7x²
∴ \(\frac{d y}{d x}\) = 0 + 2(1) – 7(2x)
= 2 – 14x
At x = – 4, \(\frac{d y}{d x}\) = 2 – (14) (- 4)
= 2 + 56 = 58 > 0
So, at x = – 4 function is increasing.
At x = 4, \(\frac{d y}{d x}\) = 2 – (14) (4) = 2 – 56 = – 54 < 0 So, at x = 4 function is decreasing.

Question 19.
Production cost of a factory producing sugar is C = \(\frac{x^{2}}{10}\) + 5x + 200. Find the marginal cost if the production is 100 units and interpret it.
Answer:
Production cost C = \(\frac{x^{2}}{10}\) + 5x + 200
∴ Marginal cost = \(\frac{d \mathrm{C}}{d x}\)
= \(\frac{d}{d x}\left[\frac{x^{2}}{10}+5 x+200\right]\)
= \(\frac{2 x}{10}\) + 5
= \(\frac{x}{5}\) + 5
If the production is x = 100, then
Marginal cost = \(\frac{100}{5}\) + 5 = 20 + 5 = 25
Interpretation: The cost of producing 101th unit will be ₹ 25.

Question 20.
The cost function of producing x units of a commodity is C = 50 + 2x + √x . Find the marginal cost if the production is 100 units and interpret it.
Answer:

Question 21.
State the method of obtaining maximum or minimum value of a function.
Answer:
Suppose, y = f(x).

• Find \(\frac{d y}{d x}\) = f’ (x) for the given function.
• Solve the equation \(\frac{d y}{d x}\) = 0 and obtain the values of x. These values are the stationary points of function.
• Obtain second order derivative \(\frac{d^{2} y}{d x^{2}}\) = f”(x).
• At the stationary value of x if \(\frac{d^{2} y}{d x^{2}}\) > 0 (Positive), then that value of x gives the minimum value of the function. Putting this value of x In the function, the minimum value of the function is obtained.
• At the stationary value of x if \(\frac{d^{2} y}{d x^{2}}\) < 0 (Negative), then that value of x gives the maximum value of the function. Putting this value of x in the function, the maximum value of the function is obtained.

Section E

Answer the following questions as required:

Question 1.
Give working rules for differentiation.
Answer:
The working rules for differentiation are as follows: u and v are differential functions of x.

Rule 1: Rule of addition and subtraction: If y = u ± v, then
\(\frac{d y}{d x}=\frac{d u}{d x} \pm \frac{d v}{d x}\)

Rule 2: Rule of multiplication : If y = u ∙ v, then
\(\frac{d y}{d x}=u \cdot\left(\frac{d v}{d x}\right)+v \cdot\left(\frac{d u}{d x}\right)\)

Rule 3: Rule of division : If y = \(\frac{u}{v}\), v ≠ 0,
then \(\frac{d y}{d x}=\frac{v \cdot\left(\frac{d u}{d x}\right)-u \cdot\left(\frac{d v}{d x}\right)}{v^{2}}\)

Rule 4: Chain rule : If y is a function of u and u is a function of x, then \(\frac{d y}{d x}=\frac{d y}{d u} \times \frac{d u}{d x}\).

Question 2.
How can it be decided using derivative that the function is increasing or decreasing at a point?
Answer:
Suppose, y = f(x) At x = a, whether f (x) is decreasing or Increasing can be decided as follows:

• At x = a, y = f(a)
• If h is a very small positive number, then when x = a + h, y = f(a + h).
• If f(a + h) > f(a) and f(a) > f(a – h). then at x = a. f(x) Is Increasing function.
• Using derivative, if f’(a) > 0, then at x = a, the function f (x) is said to be increasing function.
• If f(a + h) < f(a) and f(a) < f(a – h), then at x = a, f(x) is decreasing function.
• Using derivative, if f'(a) < 0, then the function f(x) is said to be decreasing function.

Question 3.
What is maximum value of a function ? State the conditions for maximum value.
Answer:
Suppose, y = f(x) is given function. At x = a, y = f(a). If h is a very small positive number and if f(a) > f(a + h) and f(a) > f(a – h), then the value obtained for the function at x = a is called the maximum value of function f(x).

The conditions for maximum value of function are as follows :

• Necessary condition: f'(a) = 0
• Sufficient condition : f”(a) < 0 (Negative)

Question 4.
What is minimum value of a function ? State the conditions for minimum value.
Answer:
Suppose, y =f (x) is given function.
At x = a, y = f(a). If h is very small positive number and if f(a) < f(a + h) and f(a) < f(a – h), then the value obtained for the function at x = a is called the minimum value of function f(x).

The conditions for minimum value of the function are as follows:

• Necessary condition: f’ (a) = 0
• Sufficient condition: f” (a) > 0 (Positive)

Question 5.
In a factory, production cost per hundred tons of steel is \(\frac{1}{10}\)x³ – 4x² + 50x + 300. Determine the production for minimum cost.
Answer:
Production cost C = \(\frac{1}{10}\)x³ – 4x² + 50x + 300

Conditions for minimum cost:
Necessary condition: \(\frac{d \mathrm{C}}{d x}\) = 0
∴\(\frac{3 x^{2}}{10}\) – 8x + 50 = 0
∴ 3x² – 80x + 500 = 0
∴3x² – 30x – 50x + 500 = 0
∴3x(x – 10) – 50(x – 10) = 0
∴(x – 10) (3x – 50) = 0
∴x – 10 = 0 OR 3x – 50 = 0
∴ x = 10 OR x = \(\frac{50}{3}\)

Sufficient condition:
Now, \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) = \(\frac{d}{d x}\left[\frac{d \mathrm{C}}{d x}\right]\)
= \(\frac{d}{d x}\) [3x² – 80x + 500] = 6x – 80
At x = 10,
\(\frac{d^{2} \mathrm{C}}{d x^{2}}\) = 6(10) – 80
= 60 – 80
= – 20 < 0 At x = \(\frac{50}{3}\). \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) = 6 × \(\frac{50}{3}\) – 80 = 100 – 80 = 20 > 0
Hence, when x = \(\frac{50}{3}\) hundred tons, then the production cost is minimum.

Question 6.
The cost of producing x units of an item is C = 1000 + 8x + \(\frac{5000}{x}\). What should be the production for minimum cost? Also find the minimum cost.
Answer:
The cost of producing x units of an Item,
C = 1000 + 8x + \(\frac{5000}{x}\)
∴ C = 1000 + 8x + 5000x^-1
Now, \(\frac{d \mathrm{C}}{d x}\) = 0 + 8 + (- 1) 5000x ^{– 1 – 1}
= 8 – 5000x^{– 2}
and \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) = 0 – ( – 2)5000x ^{– 2 – 1}
= 10000x ^{– 3} = \(\frac{10000}{x^{3}}\)

For minimum cost:
(1) Necessary condition:

(2) Sufficient condition:
\(\frac{d^{2} \mathrm{C}}{d x^{2}}\) > 0
\(\frac{d^{2} \mathrm{C}}{d x^{2}}\) = \(\frac{10000}{x^{3}}\)
At x = 25, \(\frac{d^{2} \mathrm{C}}{d x^{2}}\) = \(\frac{10000}{(25)^{3}}\) = \(\frac{10000}{15625}\) > 0
Hence, when production x is 25 units then the production cost is minimum.

Minimum cost:
Putting, x = 25 in C = 1000 + 8x + \(\frac{5000}{x}\)
C_min. = 1000 + 8(25) + \(\frac{5000}{25}\)
= 1000 + 200 + 200
= 1400
Hence, when production is 25 units, then minimum cost ₹ 1400.

Question 7.
Production cost function of a commodity is C = 1500 + 0.05x – 2√x. Prove that production is minimum when 400 units are produced.
Answer:
Production cost function C = 1500 + 0.05x – 2√x

For Minimum cost:

Hence, it is proved that production cost is minimum when 400 units are produced.

Question 8.
The demand function of an item is p = 30 – \(\frac{x^{2}}{10}\) Find the demand and price for maximum revenue.
Answer:
Demand function: p = 30 – \(\frac{x^{2}}{10}\)
Revenue function: R = x ∙ p
Putting. p = 30 – \(\frac{x^{2}}{10}\)

For maximum revenue:

(1)

(2) \(\frac{d^{2} \mathrm{R}}{d x^{2}}\)
\(\frac{d^{2} \mathrm{R}}{d x^{2}}\) = \(\frac{3 x}{5}\)
Putting, x = 10
\(\frac{d^{2} \mathrm{R}}{d x^{2}}\) = – \(\frac{3(10)}{5}\) = – 6 < 0
Hence, when x = 10 unit, then revenue is maximum.
Putting, x = 10 in p = 30 – \(\frac{x^{2}}{10}\)
p = 30 – \(\frac{(10)^{2}}{10}\)
= 30 – \(\frac{100}{10}\)
= 30 – 10
= 20
Hence, when demand x = 10 units and price p = 20, revenue obtained is maximum.

Question 9.
In a market, demand law of rice is x = 3(60 – p). Find the demand for maximum revenue. Also find the price and revenue for that demand.
Answer:
Demand law: x = 3(60 – p)
∴ \(\frac{x}{3}\) = 60 – p
∴ p = 60 – \(\frac{x}{3}\)

Revenue function:

For maximum revenue:
(1) \(\frac{d \mathrm{R}}{d x}\) = 0
∴ 60 – \(\frac{2 x}{3}\) = 0
∴ 60 = \(\frac{2 x}{3}\)
∴180 = 2x
∴ x = 90

(2) \(\frac{d^{2} \mathrm{R}}{d x^{2}}\) < 0
\(\frac{d^{2} \mathrm{R}}{d x^{2}}\) = – \(\frac{2}{3}\) < 0
∴ When demand x = 90 units, then revenue is maximum.
Now, putting x = 90 in p = 60 – \(\frac{x}{3}\)
p = 60 – \(\frac{90}{3}\) = 60 – 30 = 30

Maximum revenue:
Putting, x = 90 in R = 60x – \(\frac{x^{2}}{3}\).
R_max. = 60(90) – \(\frac{(90)^{2}}{3}\)
= 5400 – \(\frac{8100}{3}\)
= 5400 – 2700 = 2700
Hence, when x = 90 and p = 30 maximum revenue obtained is ₹ 2700.

Question 10.
If the demand function is p = 75 – \(\frac{x^{2}}{2500}\), then at which demand Is revenue maximum? Also find the price for maximum revenue.
Answer:
Demand functlon: p = 75 – \(\frac{x^{2}}{2500}\)
Revenue function: R = x ∙ p

For maximum revenue:

Hence, when demand x = 250 units and price p = 50 units, then maximum revenue is obtained.

Question 11.
The profit function of a producer is 40x + 10000 – 0.1x². At what production is the profit maximum? Also find this maximum profit.
Answer:
Profit function: P = 40x + 10000 – 0.1x²
∴ \(\frac{d \mathrm{P}}{d x}\) = 40 – 0.1 (2x)
= 40 – 0.2x
and \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 0.2 < 0 (Negative)

For maximum profit:
(1) \(\frac{d \mathrm{P}}{d x}\) = 0
∴ 40 – 0.2x = 0
∴ 0.2x = 40
∴ x = \(\frac{40}{0.2}\) = 200

(2) \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0
\(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 0.2<0
So, at x = 200 profit is maximum.

Maximum profit:
Putting, x = 200 in P = 40x + 10000 – 0. 1x²
P_max = 40(200) + 10000 – 0.1 (200)²
= 8000 + 10000 – 0.1 (40000)
= 18000 – 4000
= 14000
Hence, when production x = 200 units, then maximum profit obtained is ₹ 14000.

Question 12.
The profit function of a merchant is 5x – 100 – 0.01x². How many units should be produced for maximum profit?
Answer:
Profit function: P = 5x – 100 – 0.01x²
∴ \(\frac{d \mathrm{P}}{d x}\) = 5 – 0 – 0.01 (2x)
= 5 – 0.02x
and \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 0.02

For maximum profit:
(1) \(\frac{d \mathrm{P}}{d x}\) = 0
∴ 5 – 0.02x = 0
∴ 0.02x = 5
∴ x = \(\frac{5}{0.02}\) = 250

(2) \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0
\(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 0.02<0
Hence, 250 units should be produced for maximum profit.

Section F

Solve the following:

Question 1.
Find the values of x which maximize or minimize y = 2x³ – 15x² + 36x + 12. Also find the maximum and minimum values of y.
Answer:
y = 2x³ – 15x² + 36x + 12
∴ \(\frac{d y}{d x}\) = 2 (3x²) – 15′(2x) + 36 (1) + 0
= 6x² – 30x + 36
and \(\frac{d^{2} y}{d x^{2}}\) = 6(2x)-30(l) + 0
= 12x – 30
For maximum or minimum value of y,
\(\frac{d y}{d x}\) = 0
∴ 6x² – 30x + 36 = 0
∴ x² – 5x + 6 = 0
∴ x² – 3x – 2x + 6 = 0
∴ x(x – 3) – 2 (x – 3) = 0
∴ (x – 3) (x – 2) = 0
∴ x – 3 = 0 OR x – 2 = 0
∴ x = 3 OR x = 2
For maximum value of y we must have \(\frac{d^{2} y}{d x^{2}}\) < 0 and for minimum value of y, we must have \(\frac{d^{2} y}{d x^{2}}\) > 0
Now, at x = 3
\(\frac{d^{2} y}{d x^{2}}\) = 12 (3) – 30 = 36 – 30 = 6 > 0
So, at x = 3, y will be minimum.
At x = 2,
\(\frac{d^{2} y}{d x^{2}}\) = 12 (2) – 30 = 24 – 30 = – 6 < 0
So, at x = 2, y will be maximum.

Maximum value of y:
Putting, x = 2 in y = 2x³ – 15x² + 36x + 12
y_max. = 2 (2³) – 15 (2²) + 36 (2) + 12
= 2 (8) – 15 (4) + 72 + 12
= 100 – 60
= 40

Minimum value of y :
Putting, x = 3 in y = 2x³ – 15x² + 36x + 12
y_min. = 2 (3³) – 15 (3²) + 36 (3) + 12
= 2 (27) – 15 (9) + 108 + 12
= 54 – 135 + 120
= 174 – 135
= 39
Hence, at x = 2, maximum value of y obtained is 40 and at x = 3, minimum value of y obtained is 39.

Question 2.
Find the values of x which maximize or minimize f(x) = 2x³ + 3x² – 36x + 10. Also find the maximum and minimum values of f(x).
Answer:
f(x) = 2x³ + 3x² – 36x + 10
∴ f ‘(x) = 2 (3x²) + 3 (2x) – 36 (1) + 0
= 6x² + 6x – 36
and f “(x) = 6(2x) – 6(1) – 0
= 12x – 6
For maximum and minimum value of f(x), f ‘(x) = 0
∴ 6x² + 6x – 36 = 0
∴ x² + x – 6 = 0 .
∴ x² + 3x – 2x – 6 = 0
∴ x (x + 3) – 2 (x + 3) = 0
∴ (x + 3) (x – 2) = 0
x + 3 = 0 OR x – 2 = 0
x = – 3 OR x = 2

For maximum value of f(x) we must have f “(x) < 0 and for minimum value of f(x) we must have f “(x) > 0.
f “(x) = 12x – 6
At x = – 3,
f “(x) = 12 (- 3) – 6 = – 36 – 6 = – 42 < 0 So, at x = – 3, f(x) is maximum. At x = 2, f “(x) = 12 (2) + 6 = 24 + 6 = 30 > 0
So, at x = 2, f(x) is minimum.

Maximum value of f(x):
Putting, x = – 3 in f(x) = 2x³ + 3x² – 36x + 10
f(x)_max. = 2 (- 3)³ + 3 (- 3)² – 36 {- 3) + 10
= 2 (- 27) + 3 (9) + 108 + 10
= – 54 + 27 + 118 = 91

Minimum value of f(x):
Putting, x = 2 in f(x) = 2x³ + 3x² – 36x + 10
f(x)_min. = 2 (2)³ + 3 (2)² – 36 (2) + 10
= 2 (8) + 3(4) – 72 + 10
= 16 + 12 – 62 = – 34
Hence, at x = -3, maximum value of f(x) obtained is 91 and x = 2, minimum value of f(x) obtained is – 34.

Question 3.
Find the maximum and minimum values of f(x) = x³ – x² – x + 2.
Answer:
f(x) = x³ – x² – x + 2
∴ f'(x) = 3x² – 2x – 1 and f”(x) = 6x – 2
For the maximum and minimum values of f(x), f ‘(x) = 0
∴ 3x² – 2x – 1 = 0
∴ 3x² – 3x + x – 1 = 0
∴ 3x(x – 1) + 1 (x – 1) = 0
∴ (x – 1) (3x + 1) = 0
∴ x – 1 = 0 OR 3x + 1 = 0
∴ x = 1 OR x = – 1
For the maximum value of f(x) we must have f “(x) < 0 and for the minimum value of f(x) we must have f “(x) > 0.
f ”(x) = 6x – 2
At x = 1,
f”(x) = 6(1) – 2 = 4 > 0
So, at x = 1, f(x) is minimum.
At x = – \(\frac{1}{3}\)
f “(x) = 6\(\left(-\frac{1}{3}\right)\) – 2 = – 2 – 2 = – 4 < 0
So, at x = – \(\frac{1}{3}\), f(x) is maximum.

Maximum value of f(x):
Putting, x = –\(\frac{1}{3}\) in f(x) = x³ – x² – x + 2

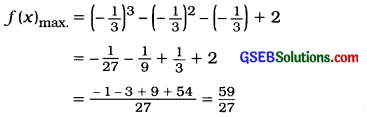
Minimum value of f(x):
Putting, x = 1 in f(x) = x³ – x² – x + 2
f(x)_min. = (1)³ – (1)² – 1 + 2
= 1 – 1 – 1 + 2 = 1
Hence, at x = – \(\frac{1}{3}\), the maximum value of f(x) obtained is \(\frac{59}{27}\) and at x = 1, the minimum value of f(x) obtained is 1.

Question 4.
A producer produces x units at cost 200x + 15x². The demand function is p = 1200 – 10x. Find the profit function and how many units should be produced for maximum profit?
Answer:
Production cost function: C = 200x + 15x²
Demand function: p = 1200 – 10x

Revenue function: R = x ∙ p
Putting, p = 1200 – 10x,
R = x (1200 – 10x)
= 1200x – 10x²

Profit function:
Profit = Revenue – Cost
P = R – C
∴ Profit function P = 1200x – 10x² – (200x + 15x²)
∴ P = 1200x – 10x² – 200x – 15x²
∴ P = 1000x – 25x²
Now, \(\frac{d \mathrm{P}}{d x}\) = 1000 – 50x and \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 50

For maximum profit:
(1) \(\frac{d \mathrm{P}}{d x}\) = 0
∴ 1000 – 50x = 0
∴ 50x = 1000
∴ x = \(\frac{1000}{50}\) = 20

(2) \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0
\(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 50 < 0
Hence, 20 units should be produced for maximum profit.

Question 5.
The selling price of a refrigerator as determined by the company is ₹ 10000. The total cost of the production for x refrigerator is C = 0.1x² + 9000x + 100 rupees. How many refrigerators should be manufactured for maximum profit?
Answer:
Total cost function : C = 0.1 x² + 9000x + 100
Selling price of one refrigerator = ₹ 10000
∴ Revenue from selling x refrigerator R = 10000x

Profit function:
P = R – C
= 10000x – (0.1 x² + 9000 x + 100)
= 10000x – 0.1x² – 9000x – 100
∴ P = 1000x – 0.1x² – 100
∴ \(\frac{d \mathrm{P}}{d x}\) = 1000 – 0.1 (2x) – 0
= 1000 – 0.2x
and \(\frac{d^{2} \mathrm{P}}{d x^{2}}\)= – 0.2

For maximum profit:
(1) \(\frac{d \mathrm{P}}{d x}\) = 0
∴1000 – 0.2x = 0
∴ 0.2x = 1000
∴ x = \(\frac{1000}{0.2}\) = 5000

(2) \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0
\(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 0.2 < 0
Hence, 5000 refrigerators should be manufactured for maximum profit.

Question 6.
A toy is sold at ₹ 20. Total cost of producing x such toys is C = 1000 + 16.5x + 0.001x² rupees. How many toys should be produced for maximum profit?
Answer:
Price of one toy = ₹ 20
∴ Revenue from selling x toys R = 20x
Total cost C = 1000 + 16.5x + 0.001x²

Profit function:
P = R – C
= 20x – (1000 + 16.5x + 0.001x²)
= 20x – 1000 – 16.5x – 0.001x²
P = 3.5x – 1000 – 0.001x²
∴ \(\frac{d \mathrm{P}}{d x}\) = 3.5 – 0 – 0.001 (2x)
= 3.5 – 0.002x
and \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 0.002

For maximum profit:
(1) \(\frac{d \mathrm{P}}{d x}\) = 0
∴ 3.5 – 0.002x = 0
∴ 0.002x = 3.5
∴ x = \(\frac{3.5}{0.002}\) = 1750

(2) \(\frac{d^{2} \mathrm{P}}{d x^{2}}\) < 0
\(\frac{d^{2} \mathrm{P}}{d x^{2}}\) = – 0.002 < 0
Hence, 1750 toys should be produced for maximum profit.