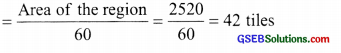Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 10 Mensuration Ex 10.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 10 Mensuration Ex 10.3
Question 1.
Find the areas of the rectangles whose sides are:
(a) 3 cm and 4 cm
(b) 12 m and 21 m
(c) 2 km and 3 km
(d) 2 m and 70 cm
Solution:
(a) ∵ Length of the rectangle = 4 cm
Breadth of the rectangle = 3 cm
∴ Area = length × breadth
= 4 cm × 3 cm = 12 sq. cm
(b) ∵ Length of the rectangle = 21 m
Breadth of the rectangle = 12 m
∴ Area = length × breadth
= 21 m × 12 m = 252 sq. m
(c) ∵ Length of the rectangle = 3 km
Breadth of the rectangle = 2 km
Area = length × breadth
= 3 km × 2 km = 6 sq. km
(d) ∵ Length of the rectangle = 2 m = 200 cm
Breadth of the rectangle = 70 cm
Area = length × breadth
= 200 cm × 70 cm = 14000 sq. cm
![]()
Question 2.
Find the areas of the squares whose sides are:
(a) 10 cm
(b) 14 cm
(c) 5 m
Solution:
(a) ∵ Side of the square = 10 cm
∴ Area of the square = side × side
= 10 cm × 10 cm = 100 sq. cm
(b) ∵ Side of the square = 14 cm
∴ Area of the square = side × side
= 14 cm × 14 cm = 196 sq. cm
(c) ∵ Side of the square = 5 m
Area of the square = side × side
= 5 m × 5 m = 25 sq. m
![]()
Question 3.
The length and breadth of the three rectangles are as given below:
(a) 9 m and 6 m
(b) 17 m and 3 m
(c) 4 m and 14 m
Which one has the largest area and which one has the smallest?
Solution:
(a) Area of rectangle = length × breadth
= 9 m × 6 m = 54 sq. m
(b) Area of rectangle = length × breadth
= 17 m × 3 m = 51 sq. m
(c) Area of rectangle = length × breadth
= 4 m × 14 m = 56 sq. m
Since, 56 > 54 > 51
∴ The rectangle (c) has the largest area and the rectangle (b) has the smallest area.
![]()
Question 4.
The area of a rectangular garden 50 m long is 300 sq. m. Find the width of the garden.
Solution:
Area of the rectangular garden = 300 sq. m
Length of the rectangular garden= 50 m
∴ The breadth of the garden = ![]()
![]()
![]()
Question 5.
What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred m sq?
Solution:
∵ Length of the rectangular plot = 500 m
The breadth of the rectangular plot = 200 m
∴ Area of the plot = length × breadth
= 500 m × 200 m = 100000 sq. m
Cost of tiling for 100 sq. m area = ₹ 8
Total cost of tiling the plot = \(\frac { 100000 }{ 100 }\) x 8
= ₹ 1000 × 8 = ₹ 8000
![]()
Question 6.
A table-top measures 2 m by 1 m 50 cm. What is its area in square metres?
Solution:
∵ 2 m by 1 m 50 cm means
Length = 2 m = 200 cm and
Breadth = 1 m 50 cm = 150 cm
∴ Area = length × breadth
= 200 cm × 150 cm = 30000 sq. cm
∴ The area of the table top = 30000 sq. cm
![]()
Note: For expressing square centimetres into square metres, we divide by 100 × 100.
![]()
Question 7.
A room is 4 m long and 3 m 50 cm wide. How many square metres of carpet is needed to cover the floor of the room?
Solution:
∵ Length of the room = 4 m = 400 cm
Breadth of the room = 3 m 50 cm = 350 cm
∴ Area of the floor of the room = length × breadth = 400 cm × 350 cm
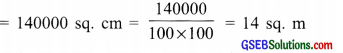
Thus, 14 sq. m of carpet is required to cover the floor of the room.
![]()
Question 8.
A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution:
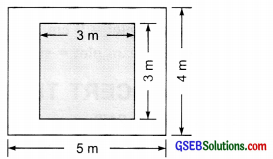
Area of the floor = length x breadth
= 5 m × 4 m = 20 sq. m
Area of the square carpet = side x side
= 3 m × 3 m = 9 sq. m
∴ Area of the floor uncovered = 20 sq. m – 9 sq m = 11 sq. m
Thus, 11 sq. m of the floor is not covered by the carpet.
![]()
Question 9.
Five square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
Solution:
∵ Length of the piece of land = 5 m
The breadth of the piece of land = 4 m
∴ Area of the piece of land = length × breadth
= 5 m × 4 m = 20 sq. m
Area of a ‘square flower bed’ = side x side
= 1 m × 1 m = 1 sq. m
∴ Area of 5 square flower beds
= 5 × 1 sq. m = 5 sq. m
∴ Area of the remaining part
= 20 sq. m – 5 sq. m = 15 sq. m
![]()
Question 10.
By splitting the following figures into rectangles, find their areas. (The measures are given in centimetres.)
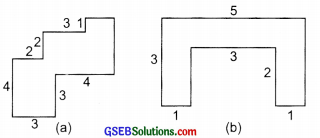
Solution:
(a) Let us split the given figure into various squares and rectangles as shown in the adjoining figure.
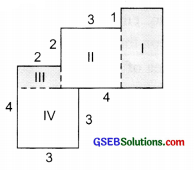
Now,
Area of rectangle I = length × breadth = 4 cm × 2 cm = 8 sq. cm
Area of square II = side × side = 3 cm × 3 cm = 9 sq. cm
Area of rectangle III = length × breadth = 2 cm × 1 cm = 2 sq. cm
Area of square IV = side × side = 3 cm × 3 cm = 9 sq. cm
∴ Total area of the figure
= 8 sq. cm + 9 sq. cm + 2 sq. cm + 9 sq. cm = 28 sq. cm
(b) Splitting the given figure ill various rectangles, we have:
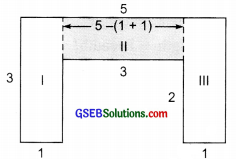
Area of rectangle I = length × breadth = 3 cm × 1 cm = 3 sq. cm
Area of rectangle II = length × breadth = 3 × 1 sq. cm = 3 sq. cm
Area of rectangle III = length × breadth = 3 × 1 sq. cm = 3 sq. cm
∴ Total area of the figure
= Area of rectangle I + Area of rectangle II + Area of rectangle III
= 3 sq. cm + 3 sq. cm + 3 sq. cm = 9 sq. cm
![]()
Question 11.
Split the following shapes into rectangles and find their areas. (The measures are given in centimetres.)
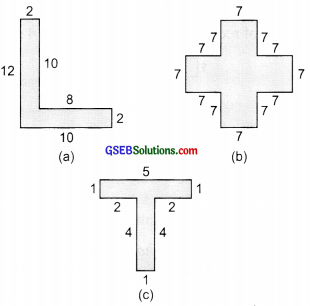
Solution:
(a) Splitting the given figure into rectangles we have,
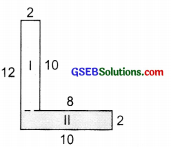
Area of rectangle I = length x breadth = 10 cm × 2 cm = 20 sq. cm
Area of rectangle II = length x breadth = 10 cm × 2 cm = 20 sq. cm
∴ Total area of the figure
= 20 sq. cm + 20 sq. cm = 40 sq. cm
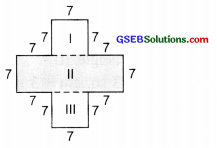
(b) Area of square I = 7 cm × 7 cm = 49 sq. cm
Area of rectangle II = (7 + 7 + 7) cm x 7 cm = 21 cm × 7 cm = 147 sq. cm
Area of square III = 7 cm × 7 cm = 49 sq. cm
∴ Total area of the given figure
= Area of I + Area of II + Area of III
= 49 sq. cm + 147 sq. cm + 49 sq. cm = 245 sq. cm
(c) Area of rectangle I = 5 cm x 1 cm = 5 sq. cm
Area of rectangle II = 4 cm x 1 cm = 4 sq. cm
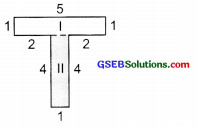
∴ Total area of the given figure = Area of rectangle I + Area of rectangle II
= 5 sq. cm + 4 sq cm = 9 sq. cm
![]()
Question 12.
How many tiles whose length and breadth are 12 cm and 5 cm respectively will be needed o fit in a rectangular region whose length and breadth are respectively:
(a) 100 cm and 144 cm
(b) 70 cm and 36 cm
Solution:
Area of the rectangular tile = 12 cm × 5 cm = 60 sq cm
(a) Area of the rectangular region = length × breadth
= 100 cm × 144 cm = 14400 sq. cm
∴ Number of tiles required to cover area of 14400 sq. cm
![]()
(b) ∵ Area of the rectangular region = length × breadth
= 70 cm × 36 cm = 2520 sq. cm
Area of the tile = 60 sq. cm
∴ Number of tiles required