Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 14 Practical Geometry Ex 14.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 14 Practical Geometry Ex 14.1
Question 1.
Draw a circle of a radius of 3.2 cm.
Solution:
Steps of construction:
Step I: Mark a point O on a paper.
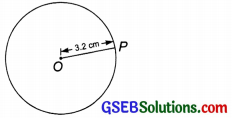
Step II: Open the compasses for the required radius of 3.2 cm.
Step III: Place the needle of the compasses at O.
Step IV: Hold the top of the compasses and move the pencil slowly till it comes back to the starting point.
The figure so obtained is the required circle having a radius of 3.2 cm.
Question 2.
With the same centre O, draw two circles of radii 4 cm and 2.5 cm.
Solution:
Steps of construction:
Step I: Mark a point O on the paper.
Step II: Open the compasses for a radius of 2.5 cm.
Step III: Keep the needle of the compasses at O.
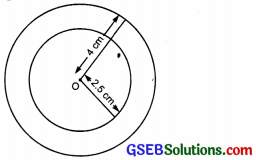
Step IV: Move the pencil and draw a circle. The circle thus, obtained is the required circle of radius 2.5 cm.
Step V: Now open the compasses for the radius of 4 cm.
Step VI: Keep the needle of the compasses again at 0 and draw a circle. The circle thus obtained is the required circle of radius 4 cm.
Note: The circles having the same centre are called concentric circles.
![]()
Question 3.
Draw a circle and any two of its diameters. If you join the ends of these diameters, what is the figure obtained? What figure is obtained if the diameters are perpendicular to each other? How do you check your answer?
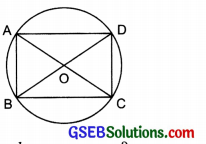
Solution:
We draw two diameters AC and BD. On joining the end-points of AC and BD we have a quadrilateral ABCD.
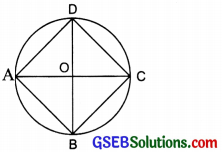
By measuring, we get
AB = CD and BC = AD
Also, ∠A = ∠B = ∠C = ∠D = 90° (each)
Thus, ABCD is a rectangle. Again, if the two diameters are perpendicular then by joining their ends, we get a quadrilateral ABCD. By measuring, we get AB = BC = CD = AD and ∠A = ∠B and ∠C = ∠D Thus, ABCD is a square.
![]()
Question 4.
Draw any circle and mark points A, B, and C such that
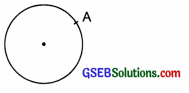
(a) A is on the circle.
Solution:
The point ‘A’ is on the circle.
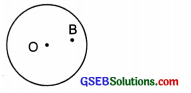
(b) B is in the interior of the circle.
Solution:
The point ‘B’ is in the interior of the circle.
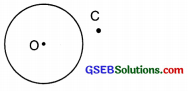
(c) C is in the exterior of the circle.
Solution:
The point ‘C’ is in the exterior of the circle.
Question 5.
Let A, B be the centres of two circles of equal radii, draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether \(\overline{\mathrm{AB}}\) and the \(\overline{\mathrm{CD}}\) at right angles.
Solution:
Yes, the line segments \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) are at right angles.
