Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 2 Whole Numbers InText Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 2 Whole Numbers InText Questions
Try These (Page 28)
Question 1.
Write the predecessor and successor of 19; 1997; 12000; 49; 100000.
Solution:

Question 2.
Is there any natural number that has no predecessor?
Solution.
Yes, the smallest natural number I has no predecessor.
Question 3.
Is there any natural number which has no successor? Is there a last natural number?
Solution:
(i) No, there is no natural number which has no successor.
(ii) No, there is no last natural number.
![]()
Try These (Page 29)
Question 1.
Are all natural numbers also whole numbers?
Solution:
Yes, all natural numbers are whole numbers.
Question 2.
Are all whole numbers also natural numbers?
Solution:
No, all whole numbers are not natural numbers. Because 0 is a whole number but it is not a natural number.
Question 3.
Which is the greatest whole number?
Solution:
Since, every whole number has a successor.
There is no greatest whole number.
![]()
Try These (Page 30)
Question 1.
Find 4 + 5; 2 + 6; 3 + 5 and 1 + 6 using the number line.
Solution:
(i) 4 + 5

Let us start from 4. Since, we have to add 5 to this number, we make 5 jumps to the right.
Each jump being equal to 1 unit. After five jumps we reach at 9 (as shown above).
4 + 5 = 9
(ii) 2 + 6

Let us start from 2. Since, we have to add 6 to this number, we make 6 equal jumps, each
jump being equal to 1 unit, to the right and reach to 8.
2 + 6 = 8
(iii) 3 + 5

We have to add 5 to 3.
We start from 3. We make 5 equal jumps. Each jump being equal to 1 unit (as shown
in the figure) to the right and reach to 8.
3 + 5 = 8
(iv) 1 + 6

As we have to add 6 to 1, therefore, we start from 1 and make 6 equal jumps to the right.
Each jump being equal to 1 unit.
We reach to 7.
1 + 6 = 7
![]()
Try These (Page 30)
Question 1.
Find 8 – 3; 6 – 2; 9 – 6 using the number line.
Solution:
(i) 8 – 3

To subtract 3 from 8, start from 8 and make 3 equal jumps towards left. Each jump being
equal to 1 unit.
So, we reach at 5, 8 – 3 = 5.
(ii) 6 – 2

To subtract 2 from 6, we start from 6. Make 2 equal jumps towards left. Each jump being
equal to 1 unit.
So, we reach at 4, 6 – 2 = 4
(iii) 9 – 6

To subtract 6 from 9, we start from 9 and make 6 equal jumps towards left. Each jump
being equal to 1 unit.
So, we reach at 3, 9 – 6 = 3
![]()
Try These (Page 31)
Question 1.
Find 2 x 6, 3 x 3; 4 x 2 using the number line.
Solution:
(i) 2 x 6

Starting from 0, move 2 units at a time to the right. Make 6 such moves.
So. we reach at 12
2 x 6 = 12
(ii) 3 x 3

Starting from 0, move 3 units at a time to the right. Make 3 such moves.
So, we reach at 9,
3 x 3 = 9
(iii) 4 x 2
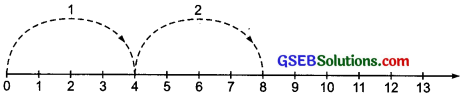
Starting from 0, move 4 units at a time to the right. Make 2 such moves.
So, we reach at 8,
4 x 2 = 8
![]()
Try These (Page 37)
Question 1.
Find: 7 + 18 + 13; 16 + 12 + 4
Solution:
(i) 7 + 18 + 13 = (7 + 13) + 18
= 20 + 18 = 38
(ii) 16 + 12 + 4 = (16 + 4) + 12
= 20 + 12 = 32
Try These (Page 37)
Question 1.
Find: 25 x 8358 x 4; 625 x 3759 x 8
(i) 25 x 8358 x 4 = (25 x 4) x 8358
(Using associativity of whole numbers)
= (100) x 8358 = 835800
(ii) 625 x 3759 x 8= (625 x 8) x 3759
(Using associativity of whole numbers)
= 5000 x 3759
= 5 x 1000 x 3759
= (3759 x 5) x 1000
= 18795 x 1001) = 18795000
625 x 3759 x 8 = 18795000
![]()
Try These (Page 39)
Question 1.
Find 15 x 68; 17 x 23; 69 x 78 + 22 x 69
using distributive property.
Solution:
(i) 15 x 68 = (10 + 5) x 68
= (10 x 68) + (5 x 68)
(By distributivity of multiplication over addition)
= 680 + 340 = 1020
(ii) 17 x 23 = 17 x (20 + 3)
= (17 x 20) + (17 x 3)
(By distributivity of multiplication Over addition)
= 340 + 51 = 391
(iii) 69 x 78 + 22 x 69 = 69[78 + 22]
= 69[100]
= 6900
69 x 78 + 22 x 69 = 6900
![]()
Try These (Page 42)
Question 1.
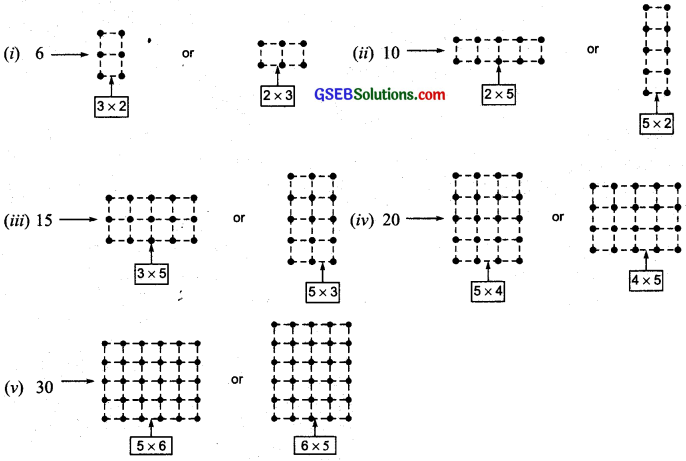
Which numbers can be shown. only as a line?
Solution:
The numbers 2, 5, 7, 11, 13, 14, 17, 19, … can be shown only as a line.
Question 2.
Which can be shown as squares?
Solution.
The numbers 4, 9, 16, 25 … .can be shown as squares.
Question 3.
Which can be shown as rectangles?
Solution:
The numbers like 4, 6, 8, 9, 10, 12, … can be shown as rectangles.
Question 4.
Write down the first seven numbers that can be arranged as triangles, e.g. 3, 6, …
Solution:
We have
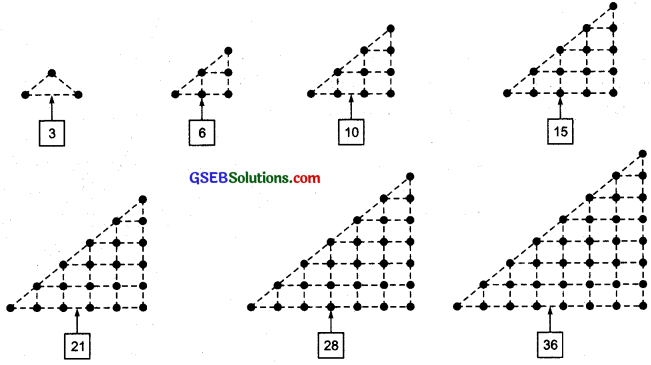
Thus, the first seven triangular numbers are: 3, 6, 10, 15, 21, 28 and 36.
![]()
Question 5.
Some numbers can be shown by two rectangles, for example,
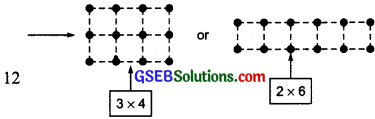
Give at least five other such examples.
Solution:
There can be many such examples. Some of them are as follows: