Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 6 Integers Ex 6.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 6 Integers Ex 6.2
Question 1.
Using the number line write the integer which is:
(a) 3 more than 5
(b) 5 more than – 5
(c) 6 less than 2
(d) 3 less than – 2
Solution:
(a) 3 more than 5:

To obtain an integer 3 more than 5, we start from 5 and move 3 units to the right of 5 and reach at 8, as shown in the figure. Thus, 3 more than 5 is 8.
(b) 5 more than – 5:

To obtain 5 more than – 5, we start from – 5 and move 5 unit to its right. We reach at 0, as shown on the number line. Thus, 5 more than – 5 is 0.
(c) 6 less than 2:

To obtain an integer 6 less than 2, we start from 2 and move 6 steps, each of 1 unit, to the left of 2. We reach at – 4, as shown in the figure. Thus, 6 less than 2 is – 4.
(d) 3 less than – 2:

To obtain 3 less than – 2, we start from – 2 and move 3 units to the left of – 2. We reach at – 5 as shown in the figure. Thus, 3 less than – 2 is – 5.
![]()
Question 2.
Use number line and add the following integers:
(a) 9 + (- 6)
(b) 5 + (- 11)
(c) (- 1) + (- 7)
(d) (- 5) + 10
(e) (- 1) + (- 2) + (- 3)
(f) (- 2) + 8 + (- 4)
Solution:
(a) 9 + (- 6)

On the number line, first we move 9 units to the right of O and reach at 9. Then, we move 6 steps to the left of 9 and reach at 3, as shown in the figure. Thus, 9 + (- 6) = +3.
(b) 5 + (- 11)
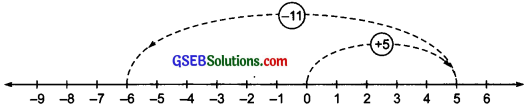
On the number line, first we move 5 units to the right of O to reach at 5. Then, we move 11 units to the left of 5 and reach at (- 6), as shown in the figure. Thus, 5 + (- 11) = – 6.
(c) (- 1) + (- 7)
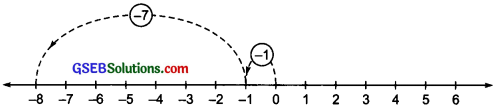
First we move 1 unit to the left of O to reach at – 1. Then, we move 7 units to the left of – 1 and reach at – 8, as shown in the figure. Thus, (- 1) + (- 7) = – 8.
(d) (- 5) + 10

First we move 5 units to the left of 0 to reach at – 5. Then, we move 10 units to the right of – 5 and reach at (+ 5), as shown in the figure, Thus, (- 5) + (10) = + 5.
(e) (- 1) + (- 2) + (- 3)

First we move 1 unit to the left of 0 and reach at (- 1). Then, we move 2 units to the left of (- 1) and reach at (- 3). Again we move 3 units to the left of – 3 and reach at – 6, as shown in the figure. Thus, (- 1) + (- 2) + (- 3) = – 6.
(f) (- 2) + 8 + (- 4)

First we move 2 units to the left of O to reach at (- 2). Then, we move 8 units to the right of (- 2) and reach at 6. Again from 6, we move 4 units to the left of 6 and reach at 2, as shown in the figure. Thus, (- 2) + 8 + (- 4) = 2.
![]()
Question 3.
Add without using number line:
(a) 11 + ( – 7)
(b) (- 13) + ( + 18)
(c) ( – 10) + (+ 19)
(d) ( – 250) + (+ 150)
(e) ( – 380) + ( – 270)
(f) ( – 217) + ( – 100)
Solution:
(a) 11 + (- 7):
Since,11 = 7 + 4
11 +( – 7) = 7 + 4 + ( – 7) = 7 + ( – 7) + 4
= 0 + 4 [ (- 7) + (7) = 0]
= + 4
Thus, 11 + (- 7) = 4
(b) ( – 13) + (+ 18):
Since, (+18) = (+13) + (+5)
( – 13) + (+18) = ( – 13) + (+ 13) + (+ 5)
= 0 + (+ 5) [( – 13) + (+ 13) = 0]
= (+5)
Thus, (- 13) + (+ 18) = 5
(c) (- 10) + (+ 19):
Since, (+ 19) = (+ 10) + (+ 9)
( – 10) + (+ 19) = (- 10) + (+ 10) + (+ 9)
= 0 + (+ 9)
[ (- 10) + (+ 10) = 0]
= + 9
Thus, ( – 10) + (+ 19) = 9
(d) ( – 250) + (+ 150):
Since, (- 250 (- 150) + (- 100)
(- 250) + (+ 150) = (- 150) + (- 100) + (+ 150)
= (- 150) + (+ 150) + (- 100) = 0 + (- 100)
[ (- 150) + ( + 150) = 0]
= – 100
Thus, ( – 250) + (+ 150) = – 100 .
(e) ( – 380) + ( – 270):
Since, the given integers are of like sign,
( – 380) + ( – 270) = – [380 + 27g] = – 650
Thus, (- 380) + (- 270) = – 650
(f) (- 217) + (- 100):
Since, the given integers are of like sign,
( – 217) + ( – 100) = – (217 + 100) = – 317
Thus, (- 217) + (- 100) = – 317
![]()
Question 4.
Find the sum of:
(a) 137 and -354
(b) – 52 and 52
(c) – 312, 39 and 192
(d) – 50, – 200 and 300
Solution:
(a) 137 + (- 354):
Since, ( – 354) = (- 137) + (- 217)
137 + ( – 354) = 137 + ( – 137) + ( – 217)
= 0 + ( – 217)
[137 + ( – 137) = 0]
= – 217
Thus, 137 + ( – 354) = – 217
(b) ( – 52) + 52:
Since, the given integers are opposite of each other, so their sum must be equal to 0.
( – 52) + 52 = 0
(c) ( – 312) + 39 + 192:
Since, 192 + 39 = 231
and (- 312) = (- 231) + ( – 81)
( – 312) + 39 + 192 = ( – 312) + 231
= ( – 231) + ( – 81) + 231
= ( – 231) + (231) + ( – 81) = 0 + ( – 81) = – 81
Thus, ( – 312) + 39 + 192 = – 81
(d) ( – 50) + (- 200) + 300:
Since, ( – 50) + ( – 200) ( – 250)
and 300 = 250 + 50
( – 50) + ( – 200) + 300 = ( – 250) + 300
= ( – 250) + 250 + 50 = 0 + 50
[( – 250) + 250 = 0]
= 50
Thus, ( – 50) + ( – 200) + 300 = 50
![]()
Question 5.
Find the sum:
(a) ( – 7) + ( – 9) + 4 + 16
(b) (37) + ( – 2) + ( – 65) + ( – 8)
Solution:
(a) ( – 7) + ( – 9) + 4 + 16:
Since, ( – 7) + ( – 9) = ( – 16)
( – 7) + ( – 9) + 4 + 16 = (- 16) + 4 + 16
= (- 16) + 16 + 4 = 0 + 4 [ ( – 16) + 16 = 0]
= 4
Thus, ( – 7) + ( – 9) + 4 + 16 = 4
(b) (37) + ( – 2) + ( – 65) + ( – 8):
Since, ( – 2) + ( – 65) + ( – 8) ( – 75)
and (- 75) = ( – 37) + ( – 38)
37 + ( – 2) + ( – 65) + ( – 8) 37 + ( – 75)
= 37 + ( – 37) + ( – 38) = 0 + ( – 38)
[37 + ( – 37) = 0]
= – 38
Thus, 37 + ( – 2) + ( – 65) + ( – 8) = – 38
![]()