Gujarat Board GSEB Solutions Class 6 Maths Chapter 7 અપૂર્ણાંક સંખ્યાઓ InText Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 7 અપૂર્ણાંક સંખ્યાઓ InText Questions
પ્રયત્ન કરો: [પાન નંબર 137]
પ્રશ્ન 1.
\(\frac{3}{5}\)ને સંખ્યારેખા પર બતાવો.
જવાબ:
આપણે જાણીએ છીએ કે \(\frac{3}{5}\) એ 0થી વધારે છે, જ્યારે 1થી ઓછા છે.
આ રીતે નક્કી થાય કે \(\frac{3}{5}\) એ 0 અને 1ની વચ્ચે છે.
હવે, \(\frac{3}{5}\)નો છેદ 5 છે, તેથી આપણે 0થી 1 વચ્ચેના ભાગના 5 ભાગ પાડીશું.
આ રીતે 0થી 1ની વચ્ચેનો દરેક ભાગ એ \(\frac{1}{5}\) છે. આથી, 3 ભાગ એ \(\frac{3}{5}\) દર્શાવે છે.

અહીં, બિંદુ A એ \(\frac{3}{5}\) દર્શાવે છે.
પ્રશ્ન 2.
\(\frac{1}{10}\), \(\frac{0}{10}\), \(\frac{5}{10}\) અને \(\frac{10}{10}\)ને સંખ્યારેખા પર બતાવો.
જવાબ:
અહીં, આપેલા અપૂર્ણાકો \(\frac{1}{10}\), \(\frac{0}{10}\), \(\frac{5}{10}\) અને \(\frac{10}{10}\) છે. જે તમામના છેદમાં 10 છે. વળી, આ બધા જ અપૂર્ણાકો છે કે 0થી વધારે છે અને 1થી ઓછા છે. તેથી સંખ્યારેખા ઉપર 0થી 1 સુધીના આપણે 10 સરખા ભાગ પાડીશું.’ એ સ્પષ્ટ છે કે દરેક ભાગ \(\frac{1}{10}\) દર્શાવે છે.
આ રીતે 1 ભાગ એ \(\frac{1}{10}\), 5 ભાગ એ \(\frac{5}{10}\) છે અને 10 ભાગ એ \(\frac{10}{10}\) દશાવે છે. \(\frac{0}{10}\) એટલે કે 0 છે.

અહીં, બિંદુ A એ \(\frac{0}{10}\), બિંદુ B એ \(\frac{1}{10}\), છે બિંદુ C એ \(\frac{5}{10}\) છે અને બિંદુ D એ \(\frac{10}{10}\) દર્શાવે છે.
![]()
પ્રશ્ન 3.
શું તમે છે અને 1ની વચ્ચે બીજો કોઈ અપૂર્ણાક દર્શાવી શકો? તમે દર્શાવી શકો એવી પાંચ અપૂર્ણાંક સંખ્યા લખો અને તેને સંખ્યારેખા પર બતાવો.
જવાબ:
હા, 0 અને 1ની વચ્ચે અસંખ્ય અપૂર્ણાંકો આવેલા છે. જુઓ નીચે સંખ્યારેખા ઉપર આવા અપૂર્ણાકો દર્શાવ્યા છેઃ

પ્રશ્ન 4.
0 અને 1ની વચ્ચે કેટલા અપૂર્ણાંકો આવે છે? વિચારો, ચર્ચા અને તમારો જવાબ લખો.
જવાબ:
0 અને 1ની વચ્ચે અસંખ્ય અપૂર્ણાંકો આવેલા છે. આ તમામનું સ્થાન સંખ્યારેખા ઉપર છે. દા. ત., \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{1}{5}\), \(\frac{2}{7}\), \(\frac{3}{9}\), \(\frac{4}{11}\), \(\frac{5}{13}\),…………. જેવા અસંખ્ય અપૂર્ણાંકો 0 અને 1ની વચ્ચે આવે છે.
પ્રયત્ન કરો: [પાન નંબર 138]
પ્રશ્ન 1.
શુદ્ધ અપૂર્ણાંક આપોઃ
(a) જેનો અંશ 5 હોય અને છેદ 7 હોય.
(b) જેનો છેદ 9 હોય અને અંશ 5 હોય.
(c) અંશ અને છેદમાં 10 સુધી ઉમેરી કેટલા આ પ્રકારના અપૂર્ણાંકો બનાવી શકો?
(d) જેનો છેદ એના અંશ કરતાં 4 ગણા જેટલો વધારે હોય.
(કોઈ પણ પાંચ અપૂર્ણાંક આપો. તમે કેટલા બનાવી શકો છો?)
જવાબ:
(a) અંશ = 5 અને છેદ = 7: માગેલો અપૂર્ણાંક = \(\frac{5}{7}\).
(b) અંશ = 5 અને છેદ = 9: માગેલો અપૂર્ણાંક = \(\frac{5}{9}\)
(c) અંશ અને છેદનો સરવાળો 10 થાય તેવી અપૂર્ણાની જોડ નીચે દર્શાવેલ છે.
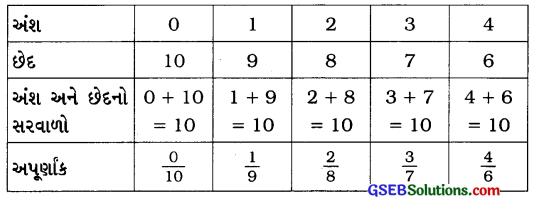
આમ, જેના અંશ અને છેદનો સરવાળો 10 થતો હોય તેવા અપૂર્ણાંકો \(\frac{0}{10}\), \(\frac{1}{9}\), \(\frac{2}{8}\), \(\frac{3}{7}\) અને \(\frac{4}{6}\) છે.
(d) જેનો છેદ એના અંશ કરતાં 4 ગણા જેટલો વધારે હોય તેવા અસંખ્ય અપૂર્ણાકો છે.
દા. ત. \(\frac{1}{4}\), \(\frac{3}{12}\), \(\frac{5}{20}\), \(\frac{7}{28}\), \(\frac{9}{36}\) . . .. (ઘણા જવાબ મળે.)
![]()
પ્રશ્ન 2.
એક અપૂર્ણાંક આપેલ છે. તેને જોઈને તમે કેવી રીતે કહી શકો કે, આ અપૂર્ણાંક –
(a) 1થી નાનો છે?
(b) 1ને સમાન છે?
જવાબ:
(a) જો અંશ < છેદ, તો અપૂર્ણાક 1થી નાનો હોય. દા. ત., \(\frac{2}{5}\) (b) જો અંશ = છેદ, તો અપૂર્ણાકની કિંમત 1 છે, જે 1ને સમાન છે. દા. ત., \(\frac{5}{5}\) પ્રશ્ન ૩. કોઈ પણ એકનો ઉપયોગ કરી ખાલી જગ્યા ભરોઃ (‘>’, “<‘ અથવા “=’)
(a) \(\frac{1}{2}\) ![]() 1
1
(b) \(\frac{3}{5}\) ![]() 1
1
(c) 1 ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
(d) \(\frac{4}{4}\) ![]() 1
1
(e) \(\frac{2005}{2005}\) ![]() 1
1
જવાબ:
નોંધઃ જો અંશ કરતાં છેદ મોટો હોય, તો અપૂર્ણાંક 1થી નાનો હોય. એટલે કે અપૂર્ણાંક < 1. જો અંશ કરતાં છેદ નાનો હોય, તો અપૂર્ણાંક 1થી – મોટો હોય. એટલે કે અપૂર્ણાંક > 1
(a) \(\frac{1}{2}\) ![]() 1
1
(b) \(\frac{3}{5}\) ![]() 1
1
(c) 1 ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
(d) \(\frac{4}{4}\) ![]() 1
1
(e) \(\frac{2005}{2005}\) ![]() 1
1
પ્રયત્ન કરો: [પાન નંબર 142]
પ્રશ્ન 1.
શું \(\frac{1}{3}\) અને \(\frac{2}{7}\); \(\frac{2}{5}\) અને \(\frac{2}{7}\); \(\frac{2}{9}\) અને \(\frac{6}{27}\) સમાન છે? કારણ આપો.
જવાબ:
(i) \(\frac{1}{3}\) અને \(\frac{2}{7}\)
1 × 7 = 7 અને 3 × 2 = 6 (ચોકડી ગુણાકાર)
હવે, 7 ≠ 6
∴ \(\frac{1}{3}\) અને \(\frac{2}{7}\) એ સમાન અપૂર્ણાંકો નથી.
![]()
(ii) \(\frac{2}{5}\) અને \(\frac{2}{7}\)
2 × 7 = 14 અને 5 × 2 = 10 (ચોકડી ગુણાકાર)
હવે, 14 ≠ 10
∴ \(\frac{2}{5}\) અને \(\frac{2}{7}\) એ સમાન અપૂર્ણાકો નથી.
(iii) \(\frac{2}{9}\) અને \(\frac{6}{27}\)
2 × 27 = 54 અને 9 × 6 = 54 (ચોકડી ગુણાકાર)
હવે, 54 = 54
∴ \(\frac{2}{9}\) અને \(\frac{6}{27}\) એ સમાન અપૂર્ણાકો છે.
પ્રશ્ન 2.
ચાર સમાન અપૂર્ણાકોનાં ઉદાહરણો આપો.
જવાબ:
સમાન હોય તેવા ચાર અપૂર્ણાકોની જોડ નીચે પ્રમાણે છે:
- \(\frac{2}{3}\), \(\frac{4}{3}\)
- \(\frac{2}{5}\), \(\frac{6}{15}\)
- \(\frac{2}{4}\), \(\frac{4}{8}\)
- \(\frac{4}{7}\), \(\frac{8}{14}\)
પ્રશ્ન 3.
દરેક અપૂર્ણાંકને ઓળખો. શું આ અપૂર્ણાકો સમાન છે?
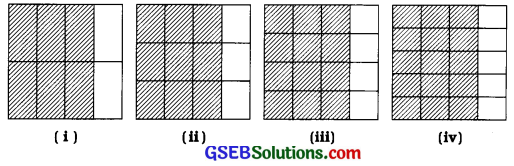
જવાબ:
(i) આકૃતિમાં કુલ 8 સરખા ભાગ છે. તેમાંથી 6 સરખા ભાગ છાયાંકિત છે.
∴ આકૃતિનો છાયાંકિત ભાગ \(\frac{6}{8}\) દર્શાવે છે.
હવે, \(\frac{6}{8}\) = \(\frac{6 \div 2}{8 \div 2}\) = \(\frac{3}{4}\)
(ii) આકૃતિમાં કુલ 12 સરખા ભાગ છે. તેમાંથી 9 સરખા ભાગ છાયાંકિત છે.
∴ આકૃતિનો છાયાંકિત ભાગ \(\frac{9}{12}\) દર્શાવે છે.
હવે, \(\frac{15}{20}\) = \(\frac{15 \div 5}{20 \div 5}\) = \(\frac{3}{4}\)
(iii) આકૃતિમાં કુલ 16 સરખા ભાગ છે. તેમાંથી 12 સરખા ભાગ છાયાંક્તિ છે.
∴ આકૃતિનો છાયાંકિત ભાગ \(\frac{12}{16}\) દર્શાવે છે.
હવે, \(\frac{12}{16}\) = \(\frac{12 \div 4}{16 \div 4}\) = \(\frac{3}{4}\)
![]()
(iv) આકૃતિમાં કુલ 20 સરખા ભાગ છે. તેમાંથી 15 સરખા ભાગ છાયાંક્તિ છે.
∴ આકૃતિનો છાયાંકિત ભાગ \(\frac{15}{20}\) દર્શાવે છે.
હવે, \(\frac{15}{20}\) = \(\frac{15 \div 5}{20 \div 5}\) = \(\frac{3}{4}\)
હવે, ઉપર (i)થી (iv)માં જોતાં દરેક અશુદ્ધ અપૂર્ણાકનું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{3}{4}\) થાય છે. તેથી બધા અશુદ્ધ અપૂર્ણાકો સમાન અપૂર્ણાકો છે.
પ્રયત્ન કરો: [પાન નંબર 143]
પ્રશ્ન 1.
નીચે આપેલામાંથી દરેકના પાંચ સમઅપૂર્ણાકો શોધો
(i) \(\frac{2}{3}\)
(ii) \(\frac{1}{5}\)
(iii) \(\frac{3}{5}\)
(iv) \(\frac{5}{9}\)
જવાબ:
નોધ સમઅપૂર્ણાંકો બનાવવા અપૂર્ણાક્ના અંશ અને છેદેને સરખી સંખ્યા વડે ગુણીશું.


પ્રયત્ન કરો: [પાન નંબર 146]
પ્રશ્ન 1.
અતિસંક્ષિપ્ત સ્વરૂપ લખો :
(i) \(\frac{15}{75}\)
(ii) \(\frac{16}{72}\)
(iii) \(\frac{17}{51}\)
(iv) \(\frac{42}{28}\)
(v) \(\frac{80}{24}\)
જવાબ:
(i) \(\frac{15}{75}\)
15ના અવિભાજ્ય અવયવો: 3, 5
75ના અવિભાજ્ય અવયવો: 3, 5, 5
∴ 15 અને 75ના સામાન્ય અવિભાજ્ય અવયવો 3, 5
∴ 15 અને 75નો ગુ.સા.અ. = 3 × 5 = 15
હવે, \(\frac{15}{75}\) = \(\frac{15 \div 15}{75 \div 15}\) = \(\frac{1}{5}\)
આમ, \(\frac{15}{75}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{1}{5}\)છે.
ટૂંકી રીત \(\frac{15}{75}\) = \(\frac{1 \times 15}{5 \times 15}\) = \(\frac{1}{5}\)
![]()
(ii) \(\frac{16}{72}\)
16ના અવિભાજ્ય અવયવો : 2, 2, 2, 2
72ના અવિભાજ્ય અવયવો 2, 2, 2, 3, 3
∴ 16 અને 72ના સામાન્ય અવિભાજ્ય અવયવો: 2, 2 અને 2
∴ 16 અને 72નો ગુ.સા.અ. = 2 × 2 × 2 = 8
હવે, \(\frac{16}{72}\) = \(\frac{16 \div 8}{72 \div 8}\) = \(\frac{2}{9}\)
આમ, \(\frac{16}{72}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{2}{9}\) છે.
ટૂંકી રીત \(\frac{16}{72}\) = \(\frac{2 \times 8}{9 \times 8}\) = \(\frac{2}{9}\)
(iii) \(\frac{17}{51}\)
17નો અવિભાજ્ય અવયવ : 17
51ના અવિભાજ્ય અવયવો: 3, 17
∴ 17 અને 51ના સામાન્ય અવિભાજ્ય અવયવઃ 17
∴ 17 અને 51નો ગુ.સા.અ. = 17
હવે, \(\frac{17}{51}\) = \(\frac{17 \div 17}{51 \div 17}\) = \(\frac{1}{3}\)
આમ, \(\frac{17}{51}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{1}{3}\) છે.
ટૂંકી રીત \(\frac{17}{51}\) = \(\frac{1 \times 17}{3 \times 17}\) = \(\frac{1}{3}\)
(iv) \(\frac{42}{28}\)
42ના અવિભાજ્ય અવયવો 2, 3, 7
28ના અવિભાજ્ય અવયવો : 2, 2, 7
∴ 42 અને 28ના સામાન્ય અવિભાજ્ય અવયવો 2, 7
∴ 42 અને 28નો ગુ.સા.અ. = 2 × 7 = 14
હવે, \(\frac{42}{28}\) = \(\frac{42 \div 14}{28 \div 14}\) = \(\frac{3}{2}\)
આમ, \(\frac{42}{28}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{3}{2}\) છે.
ટૂંકી રીત \(\frac{42}{28}\) = \(\frac{3 \times 14}{2 \times 14}\) = \(\frac{3}{2}\)
(v) \(\frac{80}{24}\)
80ના અવિભાજ્ય અવયવો 2, 2, 2, 2, 5
24ના અવિભાજ્ય અવયવો 2, 2, 2, 3
∴ 80 અને 24ના સામાન્ય અવિભાજ્ય અવયવો 2, 2 અને 2
∴ 80 અને 24નો ગુ.સા.અ. = 2 × 2 × 2 = 8
હવે, \(\frac{80}{24}\) = \(\frac{80 \div 8}{24 \div 8}\) = \(\frac{10}{3}\)
આમ, \(\frac{80}{24}\)નું અતિસંક્ષિપ્ત સ્વરૂપ \(\frac{10}{3}\) છે.
ટૂંકી રીત : \(\frac{80}{24}\) = \(\frac{8 \times 10}{8 \times 3}\) = \(\frac{10}{3}\)
![]()
પ્રશ્ન 2.
શું \(\frac{49}{64}\) એ તેના અતિસંક્ષિપ્ત સ્વરૂપમાં છે?
જવાબ:
49 = 7 × 7
64 = 2 × 2 × 2 = 2 × 2 × 2
જુઓ 49 અને 64ના અવયવોમાં કોઈ અવયવ સામાન્ય નથી.
∴ \(\frac{49}{64}\) એ અતિસંક્ષિપ્ત સ્વરૂપમાં જ છે.
પ્રયત્ન કરો: (પાન નંબર 148)
પ્રશ્ન 1.
તમે એક બૉટલ લો. એમાં \(\frac{1}{5}\) ભાગનું જ્યુસ લો અને તમારી બહેનને પણ એક બોટલ આપો તથા તેમાં \(\frac{1}{3}\) ભાગનું જ્યુસ લો. હવે, બંને બૉટલ સમાન હોય તો તમારા બંનેમાં કોનું જ્યુસ વધારે કહેવાય?
જવાબ:
આ પ્રશ્નનો ઉકેલ શોધવા એકસરખા બે લંબચોરસ લઈએ. એક લંબચોરસના 5 સરખા ભાગ કરીએ અને બીજા લંબચોરસના ત્રણ સરખા ભાગ કરીએ. હવે આપણે પ્રશ્ન સમજીએ.

આકૃતિ પરથી સ્પષ્ટ જણાય છે કે મારી બહેનનો છાયાંકિત ભાગ મારા છાયાંકિત ભાગ કરતાં વધારે છે, તેથી મારી બહેન પાસે વધુ ક્યૂસ છે.
જાણો : \(\frac{1}{5}\) અને \(\frac{1}{3}\) બંને અપૂર્ણાકોમાં અંશ સરખા છે.
જે અપૂર્ણાકનો છેદ મોટો હોય તે અપૂર્ણાક બીજા અપૂર્ણાક કરતાં નાનો હોય.
એટલે કે \(\frac{1}{5}\) < \(\frac{1}{3}\) અર્થાત્ \(\frac{1}{3}\) > \(\frac{1}{5}\)
પ્રયત્ન કરો: (પાન નંબર 149)
પ્રશ્ન 1.
નીચેનામાંથી કયો મોટો અપૂર્ણાક છે?
(i) \(\frac{7}{10}\) કે \(\frac{8}{10}\)
(ii) \(\frac{11}{24}\) કે \(\frac{13}{24}\)
(iii) \(\frac{17}{102}\) કે \(\frac{12}{102}\)
શા માટે આ સરખામણી સરળ છે?
જવાબઃ
(i) \(\frac{7}{10}\) કે \(\frac{8}{10}\)
અહીં, બંને અપૂર્ણાકોના છેદ સરખા છે તથા અંશમાં 7 < 8 છે.
∴ \(\frac{7}{10}\) < \(\frac{8}{10}\) અથવા \(\frac{8}{10}\) > \(\frac{7}{10}\)
∴ \(\frac{8}{10}\) એ \(\frac{7}{10}\) કરતાં મોટો અપૂર્ણાંક છે.
![]()
(ii) \(\frac{11}{24}\) કે \(\frac{13}{24}\)
અહીં, બંને અપૂર્ણાકોના છેદ સરખા છે તથા અંશમાં 11 < 13 છે.
∴ \(\frac{11}{24}\) < \(\frac{13}{24}\) અથવા \(\frac{13}{24}\) > \(\frac{11}{24}\).
∴ \(\frac{13}{24}\) એ \(\frac{11}{24}\) કરતાં મોટો અપૂર્ણાક છે.
(iii) \(\frac{17}{102}\) કે \(\frac{12}{102}\)
અહીં, બંને અપૂર્ણાકોના છેદ સરખા છે તથા અંશમાં 17 > 12 છે.
∴ \(\frac{17}{102}\) > \(\frac{12}{102}\) અથવા \(\frac{12}{102}\) < \(\frac{17}{102}\)
∴ \(\frac{17}{102}\) એ \(\frac{12}{102}\) કરતાં મોટો અપૂર્ણાંક છે.
અહીં, આપેલા અપૂર્ણાકોની સરખામણી ખૂબ સહેલી છે, કારણ કે આપેલા અપૂર્ણાકોની દરેક જોડમાં છેદ સરખા છે.
પ્રશ્ન 2.
નીચેના અપૂર્ણાકોને ચડતા અને ઊતરતા ક્રમમાં ગોઠવોઃ
(a) \(\frac{1}{8}\), \(\frac{5}{8}\), \(\frac{3}{8}\)
(b) \(\frac{1}{5}\), \(\frac{11}{5}\), \(\frac{4}{5}\), \(\frac{3}{5}\), \(\frac{7}{5}\)
(c) \(\frac{1}{7}\), \(\frac{3}{7}\), \(\frac{13}{7}\), \(\frac{11}{7}\), \(\frac{7}{7}\)
જવાબ:
(a) \(\frac{1}{8}\), \(\frac{5}{8}\), \(\frac{3}{8}\)
અહીં, આપેલા અપૂર્ણાકોના છેદ સરખા છે.
1, 3, 5 એ ચડતા ક્રમમાં છે તથા 5, 3, 1 એ ઊતરતા ક્રમમાં છે.
∴ અપૂર્ણાકો ચડતા ક્રમમાં કે \(\frac{1}{8}\), \(\frac{5}{8}\) અને \(\frac{3}{8}\)
અપૂર્ણાકો ઊતરતા ક્રમમાં : \(\frac{5}{8}\), \(\frac{3}{8}\) અને \(\frac{1}{8}\)
![]()
(b) \(\frac{1}{5}\), \(\frac{11}{5}\), \(\frac{4}{5}\), \(\frac{3}{5}\), \(\frac{7}{5}\)
અહીં, આપેલા અપૂર્ણાંકોના છેદ સરખા છે.
1, 3, 4, 7, 11 એ ચડતા ક્રમમાં છે તથા 11, 7, 4, 8, 1 . એ ઊતરતા ક્રમમાં છે.
∴ અપૂર્ણાકો ચડતા ક્રમમાં : \(\frac{1}{5}\), \(\frac{3}{5}\), \(\frac{4}{5}\), \(\frac{7}{5}\) અને \(\frac{11}{5}\);
અપૂર્ણાકો ઊતરતા ક્રમમાં : \(\frac{11}{5}\), \(\frac{7}{5}\), \(\frac{4}{5}\), \(\frac{3}{5}\) અને \(\frac{1}{5}\)
(c) \(\frac{1}{7}\), \(\frac{3}{7}\), \(\frac{13}{7}\), \(\frac{11}{7}\), \(\frac{7}{7}\)
અહીં, આપેલા અપૂર્ણાંકોના છેદ સરખા છે. 1, 3, 7, 11, 13 એ ચડતા ક્રમમાં છે તથા 13, 11, 7, 8, 1 એ ઊતરતા ક્રમમાં છે.
∴ અપૂર્ણાકો ચડતા ક્રમમાં : \(\frac{1}{7}\), \(\frac{3}{7}\), \(\frac{7}{7}\), \(\frac{11}{7}\) અને \(\frac{13}{7}\);
અપૂર્ણાકો ઊતરતા ક્રમમાં : \(\frac{13}{7}\), \(\frac{11}{7}\), \(\frac{7}{7}\), \(\frac{3}{7}\) અને \(\frac{1}{7}\)
પ્રયત્ન કરો [પાન નંબર 151]
પ્રશ્ન 1.
નીચેના અપૂર્ણાકોને ચડતા અને ઊતરતા ક્રમમાં ગોઠવોઃ
(a) \(\frac{1}{12}\), \(\frac{1}{23}\), \(\frac{1}{5}\), \(\frac{1}{7}\), \(\frac{1}{50}\), \(\frac{1}{9}\), \(\frac{1}{17}\)
(b) \(\frac{3}{7}\), \(\frac{3}{11}\), \(\frac{3}{5}\), \(\frac{3}{2}\), \(\frac{3}{13}\), \(\frac{3}{4}\), \(\frac{3}{17}\)
(c) હવે, ત્રણ વધુ ઉદાહરણો લખો અને તેમને ચડતા અને ઊતરતા ક્રમમાં ગોઠવો.
જવાબ:
આપણે જાણીએ છીએ કે વિષમચ્છેદી અપૂર્ણાકોમાં જ્યારે બધા અપૂર્ણાંકોનો અંશ સરખો હોય, તો જે અપૂર્ણાકનો છેદ મોટો તે અપૂર્ણાંક નાનો હોય.
(a) \(\frac{1}{12}\), \(\frac{1}{23}\), \(\frac{1}{5}\), \(\frac{1}{7}\), \(\frac{1}{50}\), \(\frac{1}{9}\), \(\frac{1}{17}\)
જુઓ 50, 23, 17, 12, 9, 7 અને 5 એ ઊતરતા ક્રમમાં છે.
∴ અપૂર્ણાકો ચડતા ક્રમમાં છે \(\frac{1}{50}\), \(\frac{1}{23}\), \(\frac{1}{17}\), \(\frac{1}{12}\), \(\frac{1}{9}\), \(\frac{1}{7}\), \(\frac{1}{5}\)
અપૂર્ણાકો ઊતરતા ક્રમમાં : \(\frac{1}{5}\), \(\frac{1}{7}\), \(\frac{1}{9}\), \(\frac{1}{12}\), \(\frac{1}{17}\), \(\frac{1}{23}\), \(\frac{1}{50}\)
![]()
(b) \(\frac{3}{7}\), \(\frac{3}{11}\), \(\frac{3}{5}\), \(\frac{3}{2}\), \(\frac{3}{13}\), \(\frac{3}{4}\), \(\frac{3}{17}\)
જુઓ 17, 13, 11, 7, 5, 4 અને 2 એ ઊતરતા ક્રમમાં છે.
∴ અપૂર્ણાંકો ચડતા ક્રમમાં \(\frac{3}{17}\), \(\frac{3}{13}\), \(\frac{3}{11}\), \(\frac{3}{7}\), \(\frac{3}{5}\), \(\frac{3}{4}\), \(\frac{3}{2}\)
અપૂર્ણાકો ઊતરતા ક્રમમાં: \(\frac{3}{2}\), \(\frac{3}{4}\), \(\frac{3}{5}\), \(\frac{3}{7}\), \(\frac{3}{11}\), \(\frac{3}{13}\), \(\frac{3}{17}\)
(c) આવાં ત્રણ બીજાં ઉદાહરણો:

જવાબ:

પ્રયત્ન કરો: (પાન નંબર 155)
પ્રશ્ન 1.
મારી માતાએ સફરજનના 4 સરખા ભાગ કરી આપ્યા. એમાંથી મને બે ભાગ આપ્યા અને મારા ભાઈને 1 ભાગ આપ્યો, તો અમારી માતાએ અમને બંનેને કુલ કેટલા ભાગ આપ્યા?
જવાબ:
માતાએ સફરજનના એક સરખા 4 ભાગ કર્યા છે.
આથી, દરેક ભાગ એ \(\frac{1}{4}\) ભાગ છે.
માતાએ મને બે ભાગ સફરજન આપ્યા છે, એટલે કે \(\frac{2}{4}\) ભાગ આપ્યો છે.
માતાએ મારા ભાઈને એક ભાગ સફરજન આપ્યું છે એટલે કે \(\frac{1}{4}\) ભાગ આપ્યો છે.
હવે, મને અને મારા ભાઈને આપેલ સફરજનના ભાગ
= \(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{2+1}{2}\) = \(\frac{3}{4}\)
આમ, માતાએ અમને બંનેને કુલ \(\frac{3}{4}\) ભાગ સફરજન આપ્યું.
![]()
પ્રશ્ન 2.
માતાએ નીલુ અને એના ભાઈને ઘઉંમાંથી કાંકરા વીણવા માટે કહ્યું. નીલુએ \(\frac{1}{4}\) કાંકરા શોધ્યા અને એના ભાઈએ પણ \(\frac{1}{4}\) કાંકરા શોધ્યા, તો તેમણે કુલ કેટલા કાંકરા (અપૂર્ણાંકમાં) શોધ્યા?
જવાબ:
નીલુએ ઘઉંમાંથી કુલ \(\frac{1}{4}\) ભાગ કાંકરા શોધ્યા.
નીલુના ભાઈએ ઘઉંમાંથી કુલ \(\frac{1}{4}\) ભાગ કાંકરા શોધ્યા.
નીલુ અને તેના ભાઈએ શોધેલા કુલ કાંકરાનો ભાગ
= \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{1+1}{4}\)
= \(\frac{2}{4}\) = \(\frac{1}{2}\)
નીલુ અને તેના ભાઈએ શોધેલા કાંકરાનો કુલ ભાગ \(\frac{1}{2}\) છે.
પ્રશ્ન 3.
સોહન એની નોટબુકને કવર ચડાવે છે. તેણે \(\frac{1}{4}\) ભાગ જેટલાં કવર સોમવારે ચડાવ્યાં. બીજા \(\frac{1}{4}\) ભાગનાં કવર મંગળવારે અને બાકીનાં બુધવારે ચડાવ્યાં, તો કેટલાં કવર (અપૂર્ણાંકમાં) બુધવારે ચડાવ્યાં હશે?
જવાબ:
સોહને સોમવારે ચડાવેલાં કવર = \(\frac{1}{4}\); સોહને મંગળવારે ચડાવેલાં કવર = \(\frac{1}{4}\)
સોહને સોમવારે અને મંગળવારે ચડાવેલાં કવર = \(\frac{1}{4}\) + \(\frac{1}{4}\)
= \(\frac{2}{4}\) = \(\frac{1}{2}\)
∴ સોહને બુધવારે ચડાવેલાં કવર = 1 – \(\frac{1}{2}\)
= \(\frac{2-1}{2}\) = \(\frac{1}{2}\)
સોહને બુધવારે \(\frac{1}{2}\) ભાગ કવર ચડાવ્યાં હોય.
![]()
પ્રયત્ન કરો: (પાન નંબર 156)
પ્રશ્ન 1.
આકૃતિની મદદથી ઉમેરો
(i) \(\frac{1}{8}\) + \(\frac{1}{8}\)
(ii) \(\frac{2}{5}\) + \(\frac{3}{5}\)
(iii) \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
જવાબ:
(i) \(\frac{1}{8}\) + \(\frac{1}{8}\)
આપણે બે સરખા લંબચોરસ દોરીશું. બંને લંબચોરસના આઠ-આઠ સરખા – ભાગ પાડીશું. આ લંબચોરસનો એક ભાગ \(\frac{1}{8}\) છે.
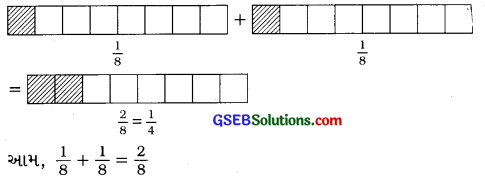
(ii) \(\frac{2}{5}\) + \(\frac{3}{5}\)
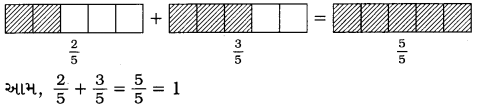
(iii) \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
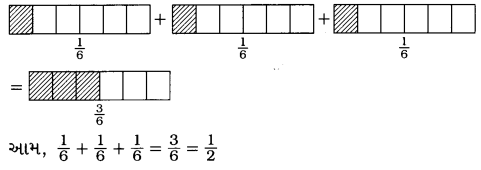
![]()
પ્રશ્ન 2.
\(\frac{1}{12}\) + \(\frac{1}{12}\) ઉમેરો.
પેપર ફોલ્ડિંગનો ઉપયોગ કરીને અને ચિત્ર દ્વારા આપણે કેવી રીતે બતાવીશું?
જવાબ:
\(\frac{1}{12}\) + \(\frac{1}{12}\) = \(\frac{1+1}{12}\) = \(\frac{2}{12}\) = \(\frac{1}{6}\)
ચિત્ર દ્વારા આ સરવાળો નીચે પ્રમાણે દર્શાવી શકાય:
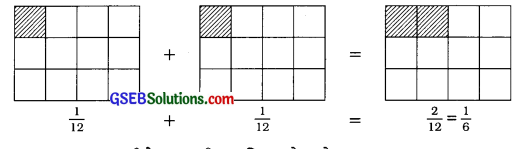
કાગળમાં ગડ વાળીને કરવાની પ્રવૃત્તિ જાતે કરો.
પ્રયત્ન કરો: (પાન નંબર 157)
પ્રશ્ન 1.
\(\frac{7}{8}\) અને \(\frac{3}{8}\) વચ્ચેનો તફાવત શોધો.
જવાબ:
\(\frac{7}{8}\) – \(\frac{3}{8}\) = \(\frac{7-3}{8}\) = \(\frac{4}{8}\) = \(\frac{1}{2}\)
\(\frac{7}{8}\) અને \(\frac{3}{8}\) વચ્ચેનો તફાવત \(\frac{1}{2}\) છે.
પ્રશ્ન 2.
માતાએ ગોળાકારમાં રોટલી બનાવી. તેના તેણે 5 ભાગમાં વિભાજન કર્યું. સીમાએ તેમાંથી એક ભાગ ખાધો. જો હું બીજો એક ભાગ ખાઈ જઉં, તો રોટલીના બીજા કેટલા ભાગો બાકી રહે?
જવાબ:
ગોળાકાર રોટલીના કુલ ભાગ = 5
∴ દરેક ભાગ = \(\frac{1}{5}\) થાય.
સીમાએ રોટલીનો ખાધેલો ભાગ = \(\frac{1}{5}\)
મેં ખાધેલી રોટલીનો ભાગ = \(\frac{1}{5}\)
સીમાએ અને મેં ખાધેલા રોટલીના કુલ ભાગ = \(\frac{1}{5}\) + \(\frac{1}{5}\)
= \(\frac{1+1}{5}\) = \(\frac{2}{5}\)
બાકી રહેલો રોટલીનો ભાગ = 1 – \(\frac{2}{5}\)
= \(\frac{5}{5}\) – \(\frac{2}{5}\) [∵ 1 = \(\frac{5}{5}\)]
= \(\frac{5-2}{5}\) = \(\frac{3}{5}\)
આમ, રોટલીનો \(\frac{3}{5}\) ભાગ બાકી રહે.
![]()
પ્રશ્ન 3.
મારી મોટી બહેને એક તરબૂચના એકસરખા 16 ભાગો કર્યા. હું તેમાંના 7 ભાગ ખાઈ ગયો અને મારા મિત્રે 4 ભાગ ખાધા, તો અમે બંને સાથે મળીને કેટલું તરબૂચ ખાધું? મેં મારા મિત્ર કરતાં કેટલું વધારે તરબૂચ ખાધું હશે? તરબૂચનો કેટલો ભાગ બાકી રહી ગયો?
જવાબ:
તરબૂચના 16 સરખા ભાગ કરવામાં આવ્યા છે.
∴ તરબૂચનો 1 ભાગ = \(\frac{1}{16}\)
મેં તરબૂચના 7 સરખા ભાગ ખાધા. એટલે કે તરબૂચનો \(\frac{7}{16}\) ભાગ ખાધો.
મારા મિત્રએ તરબૂચના 4 સરખા ભાગ ખાધા. એટલે કે તરબૂચનો \(\frac{4}{16}\) ભાગ ખાધો.
આમ, મેં અને મારા મિત્રએ ખાધેલો તરબૂચનો કુલ ભાગ = \(\frac{7}{16}\) + \(\frac{4}{16}\)
= \(\frac{7+4}{16}\) = \(\frac{11}{16}\) ………….. (i)
મારા મિત્ર કરતાં મેં વધુ ખાધેલો તરબૂચનો ભાગ = \(\frac{7}{16}\) – \(\frac{4}{16}\)
= \(\frac{7-4}{16}\)
= \(\frac{3}{16}\) ………………… (ii)
બાકી રહેલો તરબૂચનો ભાગ = 1 – \(\frac{11}{16}\)
= \(\frac{16}{16}\) – \(\frac{11}{16}\)
= \(\frac{16-11}{16}\)
= \(\frac{5}{16}\) ………………… (iii)
પ્રયત્ન કરો: (પાન નંબર 159)
પ્રશ્ન 1.
\(\frac{2}{5}\)માં \(\frac{3}{7}\) ઉમેરો.
જવાબ:
પહેલાં 5 અને 7નો લ.સા.અ. શોધીએ.

આમ, \(\frac{2}{5}\) અને \(\frac{3}{7}\)નો સરવાળો \(\frac{29}{35}\) થાય.
![]()
પ્રશ્ન 2.
\(\frac{5}{7}\) માંથી \(\frac{2}{5}\)ને બાદ કરો.
જવાબ:
પહેલાં 5 અને 7નો લ.સા.અ. શોધીએ.

HOTS પ્રકારના પ્રશ્નોત્તર
નીચેના દરેક પ્રશ્નના જવાબ માટે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ શોધીને તેનો ક્રમ-અક્ષર પ્રશ્નની સામે ![]() માં લખો :
માં લખો :
પ્રશ્ન 1.
![]()
A. 28
B. 21
C. 35
D. 20
જવાબ:
D. 20
પ્રશ્ન 2.
2\(\frac{3}{4}\) એ…………. છે.
A. શુદ્ધ અપૂર્ણાંક
B. અશુદ્ધ અપૂર્ણાંક
C. મિશ્ર અપૂર્ણાંક
D. પૂર્ણ સંખ્યા
જવાબ:
C. મિશ્ર અપૂર્ણાંક
![]()
પ્રશ્ન 3.
\(\frac{6}{15}\) …………………… \(\frac{10}{25}\)
A. >
B. =
C. <
D. ≥
જવાબ:
B. =
પ્રશ્ન 4.
……………… સમચ્છેદી અપૂર્ણાકો છે.
A. \(\frac{3}{13}\), \(\frac{4}{13}\)
B. \(\frac{5}{7}\), \(\frac{7}{5}\)
C. \(\frac{8}{9}\), \(\frac{8}{15}\)
D. \(\frac{3}{4}\), \(\frac{2}{3}\)
જવાબ:
A. \(\frac{3}{13}\), \(\frac{4}{13}\)
પ્રશ્ન 5.
\(\frac{28}{35}\)નું અતિસંક્ષિપ્ત સ્વરૂપ …………… છે.
A.\(\frac{5}{4}\)
B. \(\frac{3}{2}\)
C. \(\frac{7}{5}\)
D. \(\frac{4}{5}\)
જવાબ:
D. \(\frac{4}{5}\)
![]()
પ્રશ્ન 6.
\(\frac{3}{2}\) + \(\frac{5}{2}\) = ……………
A. 8
B. 15
C. 4
D. 16
જવાબઃ
C. 4