Gujarat Board GSEB Solutions Class 6 Maths Chapter 8 દશાંશ સંખ્યાઓ Ex 8.2 Textbook Exercise Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 8 દશાંશ સંખ્યાઓ Ex 8.2
પ્રશ્ન 1.
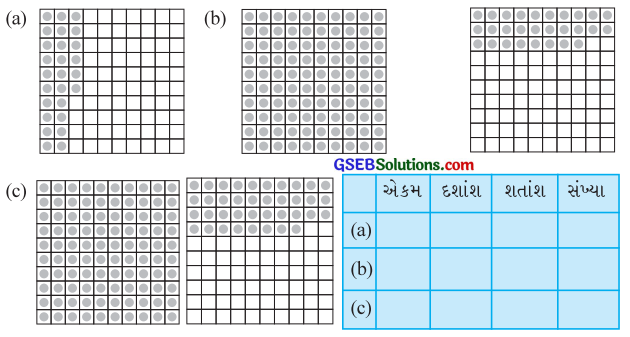
આપેલાં બૉક્સની મદદથી કોષ્ટક પૂર્ણ કરો અને દશાંશનો ઉપયોગ કરી સંખ્યા લખો :
જવાબ:
(a) અહીં, ચિત્રમાં કુલ 100 ભાગ છે. જેમાંના 26 ભાગ ડૉટેડ છે.
∴ ડૉટેડ ભાગ = \(\frac{26}{100}\) = 0.26
(b) અહીં, બે ચિત્ર આપ્યાં છે.
પહેલા ચિત્રમાં બધા જ 100 ભાગ અને બીજા ચિત્રમાં 28 ભાગ ડૉટેડ છે.
આમ, બંને ચિત્રોના થઈને કુલ ડૉટેડ ભાગ = 100 + 28
∴ ડૉટેડ ભાગ = \(\frac{100}{100}\) + \(\frac{28}{100}\) = 1 + \(\frac{28}{100}\) = 1.28
![]()
(c) અહીં, બે ચિત્ર આપ્યાં છે.
પહેલા ચિત્રમાં બધા જ 100 ભાગ અને બીજા ચિત્રમાં 38 ભાગ ડૉટેડ છે.
આમ, બંને ચિત્રોના થઈને કુલ ડૉટેડ ભાગ = 100 + 38
∴ ડૉટેડ ભાગ = \(\frac{100}{100}\) + \(\frac{38}{100}\) = 1 + \(\frac{38}{100}\) = 1.38
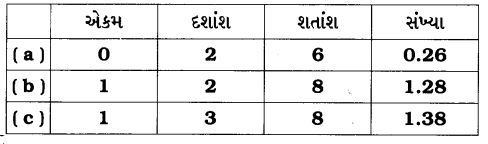
નીચે પ્રમાણે કોષ્ટકમાં રજૂઆત થાય:
પ્રશ્ન 2.
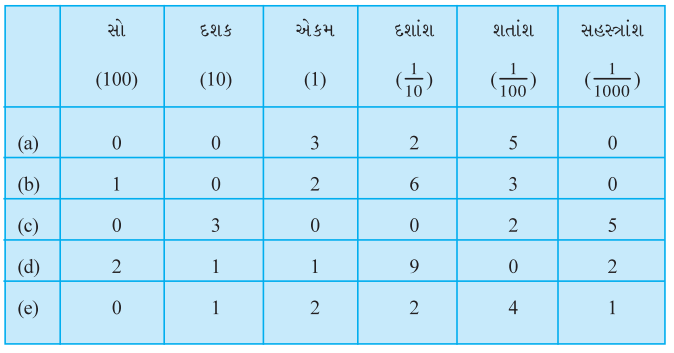
નીચે આપેલ સ્થાનકિંમત કોષ્ટકના આધારે દશાંશ સ્વરૂપમાં સંખ્યા લખો:
જવાબ:
(a) 0 સો + 0 દશક + 3 એકમ + 2 દશાંશ + 5 શતાંશ + 0 સહસ્ત્રાંશ
= 0 × 100 + 0 × 10 + 3 × 1 + 2 × \(\frac{1}{10}\) + 5 × \(\frac{1}{100}\) + 0 × \(\frac{1}{1000}\)
= 0 + 0 + 3 + \(\frac{2}{10}\) + \(\frac{5}{100}\) + \(\frac{0}{1000}\)
= 3.250 (અથવા 3.25)
(b) 1 સો + 0 દશક + 2 એકમ + 6 દશાંશ + 3 શતાંશ + 0 સહસ્રાંશ
= 1 × 100 + 0 × 10 + 2 × 1 + 6 × \(\frac{1}{10}\) + 3 × \(\frac{1}{100}\) + 0 × \(\frac{1}{1000}\)
= 100 + 0 + 2 + \(\frac{6}{10}\) + \(\frac{3}{100}\) + \(\frac{0}{1000}\)
= 102 + \(\frac{6}{10}\) + \(\frac{3}{100}\) + \(\frac{0}{100}\)
= 102.630
(c) 0 સો + 3 દશક + 0 એકમ + 0 દશાંશ + 2 શતાંશ + 5 સહસ્રાંશ
= 0 × 100 + 3 × 10 + 0 × 1 + 0 × \(\frac{1}{10}\) + 2 × \(\frac{1}{100}\) + 5 × \(\frac{1}{1000}\)
= 0 + 10 + 0 + \(\frac{0}{10}\) + \(\frac{2}{100}\) + \(\frac{5}{1000}\)
= 30 + \(\frac{0}{10}\) + \(\frac{2}{100}\) + \(\frac{5}{1000}\)
= 30.025
![]()
(d) 2 સો + 1 દશક + 1 એકમ + 9 દશાંશ + 0 શતાંશ + 2 સહસ્રાંશ
= 2 × 100 + 1 × 10 + 1 × 1 + 9 × \(\frac{1}{10}\) + 0 × \(\frac{1}{100}\) + 2 × \(\frac{1}{1000}\)
= 200 + 10 + 1 + \(\frac{9}{10}\) + \(\frac{0}{100}\) + \(\frac{2}{1000}\)
= 211 + \(\frac{9}{10}\) + \(\frac{0}{100}\) + \(\frac{2}{1000}\)
= 211.902
(e) 0 સો + 1 દશક + 2 એકમ + 2 દશાંશ + 4 શતાંશ + 1 સહસ્રાંશ
= 0 × 100 + 1 × 10 + 2 × 1 + 2 × \(\frac{1}{10}\) + 4 × \(\frac{1}{100}\) + 1 × \(\frac{1}{1000}\)
= 0 + 10 + 2 + \(\frac{2}{10}\) + \(\frac{4}{100}\) + \(\frac{1}{1000}\)
= 12 + \(\frac{2}{10}\) + \(\frac{4}{100}\) + \(\frac{1}{1000}\)
= 12.241
પ્રશ્ન 3.
નીચેના દશાંશની સ્થાનકિંમતને કોષ્ટક બનાવીને લખો:
(a) 0.29
(b) 2.08
(c) 19.60
(d) 148.32
(e) 200.812
જવાબ:
(a) 0.29 = 0 × 1 + \(\frac{2}{10}\) + \(\frac{9}{100}\)
(b) 2.08 = 2 × 1 + \(\frac{0}{10}\) + \(\frac{8}{100}\)
(c) 19.60 = 1 × 10 + 9 × 1 + \(\frac{6}{10}\) + \(\frac{0}{100}\)
(d) 148.32 = 1 × 100 + 4 × 10 + 8 × 1 + \(\frac{3}{10}\) + \(\frac{2}{100}\)
(e) 200.812 = 2 × 100 + 0 × 10 + 0 × 1+ \(\frac{8}{10}\) + \(\frac{1}{100}\) + \(\frac{2}{1000}\)
![]()
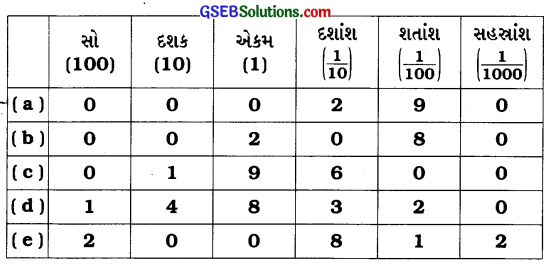
ઉપર સંખ્યાઓનું વિભાજન જાણ્યા પછી સ્થાનકિંમત કોષ્ટકમાં નીચે પ્રમાણે ગોઠવણી કરીએ :
પ્રશ્ન 4.
નીચેના દરેકને દશાંશ સ્વરૂપે લખો:
(a) 20 + 9 + \(\frac{4}{10}\) + \(\frac{1}{100}\)
(b) 137 + \(\frac{5}{100}\)
(c) \(\frac{7}{10}\) + \(\frac{6}{100}\) + \(\frac{4}{1000}\)
(d) 23 + \(\frac{2}{10}\) + \(\frac{6}{1000}\)
(e) 700 + 20 + 5 + \(\frac{9}{100}\)
જવાબ:
(a) 20 + 9 + \(\frac{4}{10}\) + \(\frac{1}{100}\)
= 29 + 4 × \(\frac{1}{10}\) + 1 × \(\frac{1}{100}\)
= 29 + 0.4 + 0.01
= 29.41
(b) 137 + \(\frac{5}{100}\)
= 137 + 0 × \(\frac{1}{10}\) + 5 × \(\frac{1}{100}\)
= 137 + 0 + \(\frac{5}{100}\)
= 137 + 0 + 0.05
= 137.05
(c) \(\frac{7}{10}\) + \(\frac{6}{100}\) + \(\frac{4}{1000}\)
= 7 × \(\frac{1}{10}\) + 6 × \(\frac{1}{100}\) + 4 × \(\frac{1}{1000}\)
= 0.7 + 0.06 + 0.004
= 0.764
(d) 23 + \(\frac{2}{10}\) + \(\frac{6}{1000}\)
= 23 + 2 × \(\frac{1}{10}\) + 0 × \(\frac{1}{100}\) + 6 × \(\frac{1}{1000}\)
= 23 + \(\frac{2}{10}\) + 0 + \(\frac{6}{1000}\)
= 23.206
(e) 700 + 20 + 5 + \(\frac{9}{100}\)
= 725 + \(\frac{0}{10}\) + \(\frac{9}{100}\)
= 725 + 0 +0.09
= 725.09
![]()
પ્રશ્ન 5.
નીચેના દરેક દશાંશને શબ્દોમાં લખો :
(a) 0.03
(b) 1.20
(c) 108.56
(d) 10.07
(e) 0.032
(f) 5.008
જવાબ:
(a) 0.03 : શૂન્ય પૉઇન્ટ શૂન્ય ત્રણ અથવા ત્રણ શતાંશ
(b) 1.20 : એક પૉઈન્ટ બે શૂન્ય અથવા એક પૂર્ણાક વીસ શતાંશ
(c) 108.56 : એક સો આઠ પૉઈન્ટ પાંચ છ અથવા એક સો આઠ પૂર્ણાક છપ્પન શતાંશ
(d) 10.07 : દસ પૉઈન્ટ શૂન્ય સાત અથવા દસ પૂર્ણાક સાત શતાંશ
(e) 0.032 : શૂન્ય પૉઈન્ટ શૂન્ય ત્રણ બે અથવા બત્રીસ સહસ્રાંશ
(f) 5.008 : પાંચ પૉઈન્ટ શૂન્ય શૂન્ય આઠ અથવા પાંચ પૂર્ણાક આઠ સહસ્રાંશ
પ્રશ્ન 6.
સંખ્યારેખા પર દશાંશ-સ્થાનનાં કયાં બે બિંદુઓ વચ્ચે નીચેની સંખ્યાઓ રહેલી છે?
(a) 0.06
(b) 0.45
(c) 0.19
(d) 0.66
(e) 0.92
(f) 0.57
જવાબ:
(a) 0.06 એ થી મોટી જ્યારે 0.1થી નાની સંખ્યા છે.
∴ 0.06 એ 0 અને 0.1ની વચ્ચે છે.
(b) 0.45 એ 0.4થી મોટી જ્યારે 0.5થી નાની સંખ્યા છે.
∴ 0.45 એ 0.4 અને 0.5ની વચ્ચે છે.
![]()
(c) 0.19 એ 0.1થી મોટી જ્યારે 0.2થી નાની સંખ્યા છે.
∴ 0.19 એ 0.1 અને 0.2ની વચ્ચે છે.
(d) 0.66 એ 0.6થી મોટી જ્યારે 0.7થી નાની સંખ્યા છે.
∴ 0.66 એ 0.6 અને 0.7ની વચ્ચે છે.
(e) 0.92 એ 0.9થી મોટી જ્યારે 1થી નાની સંખ્યા છે.
∴ 0.92 એ 0.9 અને 1ની વચ્ચે છે.
(f) 0.57 એ 0.5થી મોટી જ્યારે 0.6થી નાની સંખ્યા છે.
∴ 0.57 એ 0.5 અને 0.6ની વચ્ચે છે.
પ્રશ્ન 7.
આપેલા અપૂર્ણાકોનું અતિસંક્ષિપ્ત સ્વરૂપ લખો:
(a) 0.60
(b) 0.05
(c) 0.75
(d) 0.18
(e) 0.25
(f) 0.125
(g) 0.066
જવાબ:
(a) 0.60
= \(\frac{60}{100}\)
= \(\frac{60 \div 20}{100 \div 20}\) = \(\frac{3}{5}\) (∵ 60 અને 100નો ગુ.સા.અ. 20 છે.)
આમ, 0.60 = \(\frac{3}{5}\)
(b) 0.05
= \(\frac{5}{100}\)
= \(\frac{5 \div 5}{100 \div 5}\) = \(\frac{3}{5}\) (∵ 5 અને 100નો ગુ.સા.અ. 5 છે.)
આમ, 0.05 = \(\frac{1}{20}\)
![]()
(c) 0.75
= \(\frac{75}{100}\)
= \(\frac{75 \div 25}{100 \div 25}\) = \(\frac{3}{4}\) (∵ 75 અને 100નો ગુ.સા.અ. 25 છે.)
આમ, 0.75 = \(\frac{3}{4}\)
(d) 0.18
= \(\frac{18}{100}\)
= \(\frac{18 \div 2}{100 \div 2}\) = \(\frac{9}{50}\) (∵ 18 અને 100નો ગુ.સા.અ. 2 છે.)
આમ, 0.18 = \(\frac{9}{50}\).
(e) 0.25
= \(\frac{25}{100}\)
= \(\frac{25 \div 25}{100 \div 25}\) = \(\frac{1}{4}\) (∵ 25 અને 100નો ગુ.સા.અ. 25 છે.)
આમ, 0.25 = \(\frac{1}{4}\)
(f) 0.125
= \(\frac{125}{1000}\)
= \(\frac{125 \div 125}{1000 \div 125}\) = \(\frac{1}{4}\) (∵ 125 અને 1000નો ગુ.સા.અ. 125 છે.)
આમ, 0.125 = \(\frac{1}{4}\)
![]()
(g) 0.066
= \(\frac{66}{1000}\)
= \(\frac{66 \div 2}{1000 \div 2}\) = \(\frac{33}{500}\) (∵ 66 અને 1000નો ગુ.સા.અ. 2 છે.)
આમ, 0.066 = \(\frac{33}{500}\)