Gujarat Board GSEB Class 7 English Textbook Solutions Honeycomb Chapter 6 Expert Detectives Textbook Exercise Important Questions and Answers, Notes Pdf.
Gujarat Board Textbook Solutions Class 7 English Honeycomb Chapter 6 Expert Detectives
GSEB Class 7 English Expert Detectives Text Book Questions and Answers
Compression Check – I
Question 1.
What did Nishad give Mr Nath? Why?
Answer:
Nishad gave Mr Nath a bar of chocolate because he concluded from Mr Nath’s lean thin appearance that he was starving.
Question 2.
What is ‘strange’ about Mr Nath’s Sundays?
Answer:
Every Sunday Mr Nath used to have the same visitor at his home and the two used to have lunch together.
Question 3.
Why did Nishad and Maya get a holiday?
Answer:
It was raining heavily and the streets were flooded with the downpour. The traffic was blocked and the children got a holiday s because of all this.
Working With The Text
Question 1.
What does Nishad find out about Mr Nath from Ramesh? Arrange the information as suggested below:
(1) What he eats
(2) When he eats
(3) What he drinks and when
(4) How he pays
Answer:
(1) Mr Nath eats two chapattis, some dal and a vegetable.
(2) He eats in the morning and the evening.
(3) He drinks tea in the morning and in the afternoon.
(4) He pays in cash and also gives tips to Ramesh.
Question 2.
Why does Maya think Mr Nath is a crook? Who does she say the Sunday visitor is?
Answer:
Maya thinks that Mr Nath is a crook because he doesn’t talk to anyone and has no friends. She believes that his scars are a result of shoot-out with police. He doesn’t work ‘ anywhere and sits at home all the day and there are no visitors at his place except the guest on Sundays. He is not bothered about his meals and pays the money in cash. She! thinks that the Sunday visitor is his partner; in the crime. He keeps the money from the loot and comes to give Mr Nath his Share.
Question 3.
Does Nishad agree with Maya about Mr Nath? How does he feel about him?
Answer:
No, Nishad doesn’t agree with Maya about Mr Nath. He feels bad for Mr Nath because he thinks that he is a poor and lonely man. He also feels that he is a generous man because he gives tips to Ramesh regularly. He is determined to find why he is so thin and lonely.
Working With Language
Question 1.
The word ‘tip’ has only three letters its meanings below:
(1) fingertips
(2) the tip of your nose
(3) tip the water out of the bucket
(4) have something on the tip of your tongue
(5) tip the boat over
(6) tip him a rupee
(7) the tip of the bat
(8) the police were tipped off
(9) if you take my tip
(10) the bat tipped the ball
– but many meanings. Match the word with
– be about to say something
-make the boat overturn
-the ends of one’s fingers
-give a rupee to him, to thank him
-empty a bucket by tilting it
-the pointed end of your nose
-if you take this advice
-the bat lightly touched the ball
-the end of the bat
-the police were told or warned
Answer:
(1) fingertips – the ends of one’s fingers
(2) the tip of your nose – the pointed end of your nose
(3) tip the water out of the bucket – empty a bucket by tilting it
(4) have something on the tip of your tongue-be about to say something
(5) tip the boat over – make the boat overturn
(6) tip him a rupee – give a rupee to him, to thank him
(7) the tip of the bat-the end of the bat
(8) the police were tipped off – the police were told, or warned
(9) if you take my tip – if you take my advice
(10) the bat tipped the ball-the bat lightly touched the ball.
Question 2.
The words helper, companion, partner and accomplice have very similar meanings, but each word is typically used in certain phrases. Can you fill in the blanks below with the most commonly used words? A dictionary may help you:
1. business ……………………… .
2. my …………………… on the journey
3. I’m mother’s little ………………………… .
4. a faithful ………………….. such as dog
5. the thief’s ………………………. .
6. find a good ……………………………… .
7. tennis/golf/bridge…………………………. .
8. his ………………………. in his criminal activities
Answer:
1. partner
2. companion
3. helper
4. companion
5. accomplice
6. helper
7. partner
8. accomplice
Question 3.
Now, let us look at the uses of the word break. Match the word with its meanings below. Try to find at least three other ways in which to use the word:
(1) The storm broke
(2) daybreak
(3) His voice is beginning to break
(4) Her voice broke and she cried
(5) The heatwave broke
(6) broke the bad news
(7) break a strike
(8) Find your own expression
Answer:
(1) The storm burst into activity
(2) daybreak – the beginning of daylight
(3) His voice is beginning to break – changing as he grows up
(4) Her voice broke and she cried – could not speak; was too sad to speak
(5) The heatwave broke – this kind of weather ended
(6) broke the bad news – gently told someone the bad news
(7) break a strike – end it by making the workers submit
(8) break a promise -failed to honour a promise.
Writing
Question 1.
Who do you think Mr Nath is? Write a paragraph or two about him,
Answer:
Mr Nath is a lean and thin person. He might have met with some serious accident with fire which has resulted in many scars on his face. People are scared about him for those scars which give his face an ugly impression. He realises the same and that is why he prefers living alone and avoids going out. He talks less, but is a well-mannered person and is polite towards everyone.
He is regularly consulting Maya and Nishad’s mother, who is a doctor. Maybe he is not keeping well and that could be the reason behind his gaunt appearance. He has a friend who visits him every Sunday to find out about his health. Mr Nishad doesn’t appear to be a fastidious person. He wasn’t even quite particular about food. He eats the same kind of food every day.
Question 2.
What else do you think Nishad and Maya will find out about him. ? How? Will they ever be friends? Think about these questions and write a paragraph or two to continue the story.
Answer:
Nishad and Maya would have found out that the Sunday visitor is Mr Nath’s brother. Mr Nath used to work for a big private company and has left the job for a while because he was not keeping well. He is suffering from some liver ailment and will be undergoing a surgery soon.
Nishad succeeds in befriending him and goes to his house every evening to play with him. He finds Mr Nath a caring and loving person. He becomes a frequent visitor to his place. Maya regrets about her earlier thoughts about Mr Nath. She feels sorry about It. Nishad takes her along one day and then they all become friends.
Question 3.
Conducting a Survey:
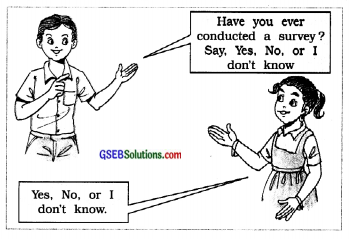
Step I: Study the following questionnaire and discuss the points in, small groups.
A home is a place where
you feel secure and happy.
you can be alone.
you can keep all your things.
you can bring up a family.
you can invite friends/relatives.
A home is a place where
you can make a noise if you want to.
you can do whatever you like.
you are at peace.
you can look after your parents.
you receive and give love.
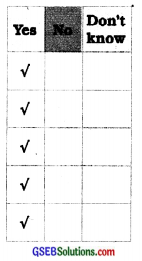
Step II: Collect information. Contact people in the school / your locality and put these questions to them. Tick-mark (V) their answers in the relevant column.
Step III: Analyse the results in the group by asking
How many people think that a home is a place where you feel secure and happy?
How many people think that a home isn’t a place where you feel secure and happy?
How many people don’t know about it?
Step IV: Present a brief oral report on the result of your survey. Use phrases such as the following
Most people think that…
Few people think that…
Hardly anyone thinks that…
No one thinks that…
Answer:
Students will carry out these activities (Steps II, III and IV) themselves.
Speaking
Play detectives with each other. Find a person in your class (or some other acquaintance) to speak to. Find out the answers to the questions given below. Be careful to ask your questions in. a polite and inoffensive way. Do not force the person to answer you. Then allow the person to ask you the same questions.
(i) Name?
(ii) What newspapers or magazines does the person read?
(iii) How long has the person lived at the current address?
(iv) What does she/he do during the day, I.e. the daily routine?
(v) What do neighbours and friends say about the person?
(vi) Who are his/her visitors and what are his/her eating habits? (You can ask a few others about this.)
(vii) What do you think about the person?
Answer:
Do it yourself.
GSEB Class 7 English Expert Detectives Additional Important Questions and Answers
Select the most appropriate options as answers and complete the following sentences :
Question 1.
Nishad was called ‘Seven’ because…
A. he was seven years old.
B. he had seven plans to trap the crook.
C. Nishad means the seventh note on the musical scale.
D. Nishad had seven friends.
Answer:
C. Nishad means the seventh note on the musical scale.
Question 2.
What was Seven’s guessing about Nath’s being thin?
A. He had some disease.
B. He was poor and could not afford to eat.
C. He did not do any exercise.
D. None of these three.
Answer:
B. He was poor and could not afford to eat.
Question 3.
The clinic belonged to ………………….. .
A. Nath.
B. Ramesh.
C. Nishad’s mother.
D. Mr Mehta.
Answer:
C. Nishad’s mother.
Question 4.
According to Maya, Nath ………………. .
A. had got millions of rupees.
B. had hidden lots of money somewhere.
C. had collected money by unfair means.
D. All of these three.
Answer:
D. All of these three.
Question 5.
What scars were there on Nath’s face, according to Nishad’s mother?
A. Burn scars.
B. Scars got in police shoot-out.
C. Cut-marks of a fall.
D. Both ‘A’ and ‘B’.
Answer:
A. Burn scars.
Question 6.
That day there was an unexpected holiday because of ……………………. .
A. somebody’s death.
B. heavy downpour.
C. some riots in the city.
D. None of these three.
Answer:
B. heavy downpour.
Question 7.
Alias’ means …………………….. .
A. an alternate name.
B. the name in police records.
C. an accomplice in crime.
D. a nickname given by friends.
Answer:
A. an alternate name.
Question 8.
According to Maya, ……………………. might be the accomplice of Nath.
A. Ramesh
B. Mr Mehta
C. his Sunday visitor
D. Seven
Answer:
C. his Sunday visitor
Question 9.
What did Nishad do when he happened to visit Nath’s house one day?
A. He was greatly scared to see him.
B. He fought with him.
C. He gave him a chocolate bar.
D. He asked him how he had scars on his face.
Answer:
C. He gave him a chocolate bar.
Question 10.
One of the following is not the finding regarding Nath:
A. He lived in Shankar house.
B. He kept on quarrelling with other tenants.
C. He didn’t receive any letters.
D. He didn’t work and kept on sitting in the room all day.
Answer:
B. He kept on quarrelling with other tenants.
Say whether the following sentences are True or False:
Question 1.
Nishad did not agree with Maya In her assumptions about Mr Nath.
Answer:
True
Question 2.
Nishad’s mother was a detective.
Answer:
False
Question 3.
Every Sunday a spectacled, atman visited Mr Nath at its place.
Answer:
True
Question 4.
Nishad had prepared a list of facts about Mr Nath.
Answer:
False
Question 5.
The people In Shankar House were all scared of Mr Nath according to the list.
Answer:
True
Question 6.
According to Nishad. Mr Nath was a bad man.
Answer:
False
Question 7.
Nishad proposed that he would like to be Nath’s friend.
Answer:
True
Question 8.
Nath was a patient of Nishad’s mother.
Answer:
True
Answer the following questions In two to three sentences each:
Question 1.
What made Nishad turn sympathetic towards Mr Nath?
Answer:
Nishad turned sympathetic towards Mr Nath seeing his gaunt appearance. His attitude changed further when he came to know that he used to give regular tips to Ramesh for bringing his food. Then he also remembered his mother’s words that Mr Nath was a polite man.
Question 2.
Give a brief description about Mr Nath’s visitor.
Answer:
Mr Nath used to have a visitor on every Sunday. He was a spectacled, tall, fair and stout man. Ramesh found him talking a lot. He used to give company to Mr Nath for lunch during his visits.
Question 3.
What was Maya doing on her unexpected holiday?
Answer:
On her unexpected holiday. Maya assigned herself the task of solving the mystery of Mr Nath. She was busy noting down all the available facts about Mr Nath. She then shared with his brother and asked for his opinion.
Question 4.
What did Maya think about Mr Nath’s visitor?
Answer:
Maya thought that Mr Nath’s visitor was his accomplice in his crimes. She believed that he kept all the loot with him and used – to -come now and then to give his partner his share so that he could manage his expenses.
Answer the following questions in four, to five sentences each:
Question 1.
Describe Nishad as a child.
Answer:
Nishad as a child was kind and considerate. He kept in mind all the good things his mother and Ramesh told him about Mr Nath and formed his opinion based on them. He was upset with Mr Nath being so lean and thin. He thought that the man might be starving so he went to his place and gave him a bar of chocolate. He refused calling him a crook even after being insisted several times by his sister and decided to befriend him because he liked him.
Question 2.
What all facts Maya collected about Mr Nath?
Answer:
Maya collected the following facts: His name was Mr Nath and they must find out his first name. Other tenants at Shankar House called him mad, strange and unfriendly. He didn’t speak with anyone and lacked manners. He never received any letters and has been living as tenant in Room No. 10 in Shankar House. He didn’t go to work anywhere and stayed in his room the whole day.
All the kids and some of the grown-up people in Shankar House were scared of him. He had no visitors except the same man on every Sunday. Ramesh brought his food from the restaurant downstairs and Mr Nath was not much bothered about what he ate. He settled the bills by paying cash and tipped Ramesh liberally.
Read the following passages carefully and answer the questions given below them:
Question 1.
“But- Maya, Mr Mehta told us he doesn’t work anywhere, so how can he possibly have money to pay for food?” Nishad said.
“Exactly!” I exclaimed. “He must have lots
of money hidden somewhere, maybe in that trunk in his room. It’s probably full of silver and gold and jewels and…”
“What rubbish,” Nishad interrupted.
“I know I’m right, stupid,” I told him. “By the way, Seven, did you see his scars? I couldn’t, it was too dark, but I bet he got them during a shoot-out with the police or something.”
“Mummy told us quite clearly they were burn scars,” Nishad said firmly.
Questions :
(1) What doubt does Nishad raise about Nath’s paying for food?
Answer:
Nishad doubts that Nath cannot have money to pay for food as he doesn’t work anywhere.
(2) What does Nishad term as ’rubbish’?
Answer:
Maya says that Mr Nath must have lots of money hidden somewhere, maybe in that trunk in his room. It’s probably full of silver and gold and jewels, etc. Nishad terms this assumption of Maya ‘rubbish.
(3) What is Maya’s guess about the scars on Nath’s face?
Answer:
Maya guesses that Nath must have those scars on his face during a shoot out with the police or something.
(4) What does the phrase ’by the way’ mean?
Answer:
The phrase ‘by the way’ means S ‘incidentally’.
Question 2.
“Ramesh told me something very strange, Maya,” Seven added. “Almost every? Sunday, he carries two lunches to Mr Nath’s room and the same man is with him each? time. He’s’tall, fair, stout and wears spectacles. Ramesh says his visitor talks a lot, unlike Mr Nath who hardly speaks.” “Well done, Nishad,” I told him. “Now, that we’ve made some progress with our inquiries, we’ll have to sort out all the facts like expert detectives so that we can trap the crook.”
“How you do go on, Maya,” Seven sighed. “How can you possibly imagine he’s a crook? He looks so ordinary!”
“Criminals can look quite ordinary, smarty,” I retorted. “Did you see the picture of the Hyderabadi housebreaker in the papers yesterday? He looked like any man on the street.” Nishad looked doubtful.
Questions:
(1) What sounded strange to Nishad?
Answer:
Every Sunday the same man visited Mr Nath. This sounded strange to Nishad because otherwise, Mr. Nath was very unfriendly.
(2) Pick out the difference in nature of Mr Nath and his Sunday visitor.
Answer:
The visitor talked a lot while Mr Nath hardly spoke anything.
(3) How did Maya counter Nishad about Mr Nath?
Answer:
Nishad told, whom Maya took to be a crook, was an ordinary-looking person. Maya countered that criminals can look quite ordinary.
(4) Pick out words from the passage with the following meanings:
(i) strong or sturdy
(ii) responded
Answer:
The words are :
(i) stout
(ii) retorted
Question 3.
“How can a crook have friends, idiot ?” I almost shouted. “At least he has one friend, the one who meets him on Sundays,” said Nishad. A brilliant thought occurred to me just then. “That man must be Mr Nath’s accomplice in crime,” I said. “Maybe he keeps all the loot and he comes now and then to give part of it to his partner, Mr Nath, for expenses.
That’s It! Fm sure I’m right.” if you insist on calling him a criminal. I don’t think I want to discuss anything with you. Maya.” said Nishad angrily. “He can’t be such a bad man 1f he gives Ramesh such generous tips.”
‘Ramesh probably knows something about his past, so Mr Nath must be bribing him to keep quiet,” I said. ‘ Nishad glared at me with his arms tightly crossed across his chest. T was beginning to get fed up with hIm.
Questions:
(1) Who could be Nath’s accomplice in crime, according to Maya?
Answer:
According to Maya, the person who visited Nath every Sunday regularly could be Nath’s accomplice in crime.
(2)How did his partner help Nath?
Answer:
According to Maya, Nath’s partner might be keeping all the loot and visiting him every Sunday to give a part of It.
(3) What made Nishad angry?
Answer:
Maya kept on insisting that Nath was a criminal without any evidence, therefore Nishad got angry with her In disagreement.
(4) Why, according to Maya, did Ramesh not talk much about Nath?
Answer:
According to Maya, Ramesh did not talk much about Nath as Nath must be bribing him.
Vocabulary
Replace the underlined words selecting the most appropriate options from the brackets :
(1) The escaped convicts have been on the run for a week. (running constantly, avoiding capture, chasing others)
(2) Please stash this away somewhere; you may need it someday. (hide, save, block)
(3) The jeweller sorted the diamonds out by weight and clarity. (polished, fixed, classified)
Answer:
1. The escaped convicts have been avoiding capture for a week.
2. Please hide this somewhere; you may need it someday.
3. The jeweller classified the diamonds by weight and clarity.
Choose the correct words from the brackets and complete the following passage:
Question 1.
(knocked, starving, gaunt, quickly, upset, sure)
Seven had been quite ……………………….. about Mr Nath’s ………………………. appearance and was ………………….. that he was ………………………………….. He told me that he had …………………………. loudly on Mr Nath’s door that evening and said, “Open the door …………………… Mr Nath.”
Answer:
Seven had been quite upset about Mr Nath’s gaunt appearance and was sure that he was starving. He told jne that he had knocked loudly on Mr Nath’s door that evening and said, “Open the door quickly, j Mr Nath.”
Question 2.
(Almost, same, hardly, something, stout, carries)
“Ramesh told me ……………………………… very strange, Maya,” Seven added. “………………………… every Sunday, He’s tall, fair, ………………………….. and wears spectacles. Ramesh says his visitor talks a lot, unlike Mr Nath who ………………… speaks.”
Answer:
“Ramesh told me something very strange, Maya,” Seven added. “Almost every Sunday, he carries two lunches to Mr Nath’s room and the same man is with him ’ each time. He’s tall, fair, stout and wears spectacles. Ramesh says his visitor talks a lot, unlikes Mr Nath who hardly speaks.”
Grammar
Choose the correct Article(s), Conjunction(s) and Preposition (s) and complete the following passage:
Question 1.
On the Monday following Mamma’s birthday, Seven went alone ………………….. her to the clinic at Girgaum ……………………….. I was spending the evening with ……………………….. schoolfriend. ………………………. they returned, Nishad told me he’d been to see Mr Nath ……………………… I felt most annoyed ……………………. I hadn’t been there.
Answer:
On the Monday following Mamma’s birthday, Seven went along with her to the clinic at Girgaum as was spending the evening with a school friend. When they returned, Nishad told me he’d been to see Mr Nath and felt most annoyed that hadn’t been there.
Question 2.
“ ……………………….. you insist ……………………….. calling him a criminal, I don’t think I want to discuss anything ……………………… you, Maya,” said Nishad angrily. “He can’t be such ……………………….. bad man if he gives Ramesh such generous tips.”
“Ramesh probably knows something …………………………….. his past, so Mr Nath be bribing him ………………………… keep quiet,” I said.
Answer:
“If you insist on calling him a criminal, I don’t think I want to discuss anything with; you, Maya,” said Nishad angrily. “He can’t be s such a bad man if he gives Ramesh such generous tips.”
“Ramesh probably knows something about his past, so Mr Nath must be bribing him s to keep quiet,” I said.
Fill in the blanks with the appropriate forms of verbs given in the brackets and complete the texts:
Question 1.
When they returned, Nishad told me he’d been ………..1………… (see) Mr Nath and I ……………2…………….. (feel) most annoyed that I …………3…………. (not + be) there.
Answer:
1. to see
2. felt
3. hadn’t been
Question 2.
He told me that he ……….1………. (knock) loudly on Mr Nath’s door that evening and ……….2………… I (say), “ ……..3……. (open) the door quickly, Mr Nath.”
Answer:
1. had knocked
2. said
3. Open
Change the voice of the following :
(1) The police had to set his house on fire.
(2) Me had obviously recognised my brother.
(3) Did you get a chance to peek into the trunk?
(4) I hope you questioned him properly.
(5) Ramesh told me something very strange,
(6) We’ll have to sort out all the facts.
(7) Did you see the picture of the Hyderabadi housebreaker in the papers yesterday?
(8) Have I forgotten anything, Seven?
Answer:
(1) His house had to be set on fire by the police.
(2) My brother had obviously been s recognised by him.
(3) Was a chance to peek into the trunk S got by you?
(4) I hope he was questioned properly by you.
(5) I was told something very strange by Ramesh.
(6) All the facts will have to be sorted out by us.
(7) Was the picture of Hyderabadi s housebreaker seen by you in the papers? yesterday?
(8) Has anything been forgotten by me, Seven?
Turn the following dialogue into Indirect Speech:
Question 1.
“What rubbish,” Nishad interrupted. “I know I’m right, stupid,” I told him. “By the way, Seven, did you see his scars ?”
“Mummy told us quite clearly they were s burn scars,” Nishad said firmly.
“Perhaps the police had to set his house ] on fire to force him out,” I suggested.
Answer:
Nishad interrupted with great dislike ? that it was quite rubbish. Then calling him stupid, I told him that knew was right. Then shifting the topic of the talk I asked Seven if he had seen his scars. Nishad firmly said that his mummy had told them quite clearly they were burn-scars. Then I expressed my guessing that perhaps the police had to s set his house on fire to force him out.
Question 2.
The man had opened it and asked him, “Lost another marble?”
“No,” said Nishad.
“Did you get a chance to peek into the trunk, Seven?” I asked.
Answer:
The man had opened it and asked him if he had lost another marble. Nishad replied negatively. Then I asked Nishad calling him Seven if he had got a chance to peek into the trunk.
Rewrite as directed :
(1) He can’t be poor if he’s a crook on the run. (Use ‘unless’.)
(2) Mr Mehta told us he doesn’t work anywhere. (Turn into Affirmative.)
(3) Seven had been quite upset about Mr Nath’s gaunt appearance. (Turn into Exclamatory.)
(4) Mr Nath pays cash and tips well. (Use ‘not only … but …’.)’
(5) We’ll have to sort out all the facts like expert detectives so that we can trap the crook. (Remove ‘so that’.)
(6) Since he was under Mamma’s medical treatment, he had to be polite. (Use ‘because’.)
(7) How can a crook have friends? (Turn into Affirmative.)
(8) Ramesh probably knows something about his past. (Use ‘may’.)
Answer:
(1) He can be poor unless he’s a crook on the run.
(2) Mr Mehta told us he is jobless.
(3) How upset Seven had been about Mr Nath’s gajnnt appearance!
(4) Mr Nath not only pays cash but tips well too.
(5) We’ll have to sort out all the facts like expert detectives to trap the crook.
(6) He had to be polite because he was under Mamma’s medical treatment.
(7) A crook cannot have friends.
(8) Ramesh maybe knows something about his past.
Message Writing
Question 1.
You receive a telephone call from your mother’s office when she is not at home. You have the following conversation with the speaker. But you have to go for your tuition class. So you leave a message for your mother. Write the message within 50 words using the information given below. Do not add any new information.
Answer:
Anik: Hello!
Mr Shah: Hello! May I speak to Mrs Dixit, please? I am Mayank Shah from the office.
Anik: Mom’s not at home right now.
Mr Shah: In that case can you give her a message? It is urgent. Please tell her that the meeting fixed for tomorrow has been rescheduled. Ask her to check her mail as soon as possible for the details. Please don’t forget to inform her.
Anik: Don’t worry. I will tell her as soon as she returns.
14, Feb. 3:30 pm
Mom, Mr Mayank Shah from the office called up to say that the meeting fixed for tomorrow has been rescheduled. He wants you to check your mail as soon as possible for the details. He said it was urgent.
Question 2.
Mrs Dayal wants to speak to her son, Rishi. As Rishi is not in his seat in! office, you take the call and speak to her. s She wants to inform Rishi that she will be coming to Delhi the next evening and that she should pick her up from the airport. You want to know by which flight she will be arriving. She replies that she would be s coming by Jet Airways flight no. 7W122.
She thanks you and asks you your name. You tell her that your name is Ayan and I assure her that you will convey her message to Rishi. But you yourself have a meeting to attend. So you leave a note for Rishi. Write this message in not more than 50 words.
Answer:
15, June 3:30 pm
Rishi, your mother called up to say that she’s arriving by Jet Airways flight no. 7W122 !; tomorrow evening. She wants you to receive her at the airport. Ayan
Expert Detectives Summary in English
Expert DetectivesSummary:
Nishad and his 10-year-old sister Maya have always been inquisitive about their neighbour Mr Nath. One day their marbles go inside his house and Nishad gets a chance to catch a glimpse of Mr Nath. To Nishad, Mr. Nath appears to be a crook running away from the cops. He has a bad scar on his face and doesn’t have any friends. But Mr Nath is a patient of their mother who is a doctor by profession.
Their mother has told them that he is a polite man. Nishad is also called Seven because his name means the seventh note on the musical scale. The two children are busy discussing their mysterious neighbour. They argue about his financial wealth, how he manages his food and so on. Nishad thinks that he is poor and doesn’t have much money while Maya believes that he has got a lot of money and has kept it hidden somewhere in his room. Then, it is Mr Nath’s scar that bothers the children.
They think that he might have got it during a shoot-out with the police. On the following Monday after their mother’s birthday, Nishad goes along with her to the clinic. He happens to see Mr Nath there. He is worried seeing Mr Nath’s gaunt appearance. That evening Nishad goes to Mr. Nath’s place and gives a bar of chocolate to him. Nishad befriends Ramesh, the boy who brings food for Mr Nath from a nearby restaurant.
Ramesh informs him that Mr Nath has two meals a day and tea in the morning and in the afternoon. His meal is the same every day and always used to pay in cash and tips as well. He brings two lunches on Sundays and it is the same visitor he finds there. The visitor is a tall, stout and spectacled man who talks a lot while Mr Nath is a quiet person. The children are thrilled and they are discussing the possibilities of Mr Nath being a crook. Their school opens after the summer holidays the next day but they Cannot attend it because of heavy rains.
Nishad is busy reading his comics when Maya informs what she has done. She has made a note of everything they know about Mr Nath calling them facts and gives a number to each one of them. Nishad disagrees with calling Mr Nath a criminal. He feels bad for Mr. Nath for having no friends while Maya thinks that the visitor who comes to his place on Sundays may be his partner who knows all his secrets and maybe about the loot as, well. Both the children have an argument and Nishad Is upset with Maya for calling Mr Nath a crook. Nishad is Interested only In finding out why Mr Nath is so thin and a loner. He wants to be his friend and Mayas theories don’t have any impact on Seven.