Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 14 Symmetry InText Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 14 Symmetry InText Questions
![]()
Try These (Page 272)
Question 1.
(i) Can you now tell the order of the rotational symmetry for an equilateral triangle? (Look at the following figures.)
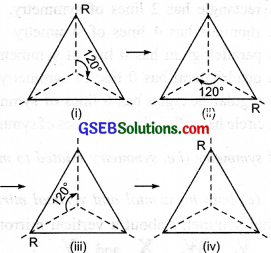
(b) How many positions are there at which the triangle looks exactly the same, when rotated about its centre by 120°?
Solution:
(a) ∵ There are exactly three positions where the triangle looks the same.
∴ It has a rotational symmetry of order 3.
(b) There is only one position where the triangle looks exactly the same, when rotated about its centre through 120°.
![]()
Question 2.
Which of the following shapes have rotational symmetry about the marked point?
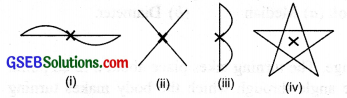
Solution:
All the above shapes, i.e. (i), (ii), (iii) and (iv) have rotational symmetry about the marked point (X).
Do This (Page 272-273)
Draw two identical parallelograms, one ABCD on a piece of paper and the other A’ B’ C’ D’ on a transparent sheet. Mark the points of intersection the parallelograms such that A’ lies on A, B’ lies on B and so on. O’ then falls on O. Stick a pin into the shapes at the point O.
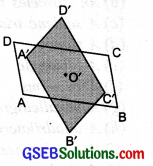
Now turn the transparent shape in the clockwise direction.
(i) How many times do the shapes coincide in one full round?
(ii) What is the order of rotational symmetry?
Solution:
(i) Let us turn the transparent shape in the anti-clockwise direction. We see that there are two positions: First, when A’ is on A and Second, when A’ falls on C. This shows that in a full turn (of 360°) the parallelogram has two positions, where it looks exactly the same.
(ii) The parallelogram has rotational symmetry of order 2.
Note : In this case the point where we have the pin is the centre of rotation. It is the meeting point of the diagonals.
![]()
Try These (Page 273)
Question 1.
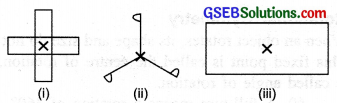
Give the order of the rotational symmetry of the given figures about the point marked.
Solution:
(i) The order of rotational symmetry is 4.
(ii) The order of rotational symmetry is 3.
(iii) The order of rotational symmetry is 4.
Note : Every object has a rotational symmetry of order one, because it occupies the same position after a rotation of 360°, i.e. after a complete revolution.
![]()
Do This (Page 275)
Question 1.
Some of the English alphabets have fascinating symmetrical structures. Which capital letters have just one line of symmetry (like E)? Which capital letters have a rotational symmetry of order 2 (like I)?
By attempting to think on such lines, you will be able to fill in the following table:
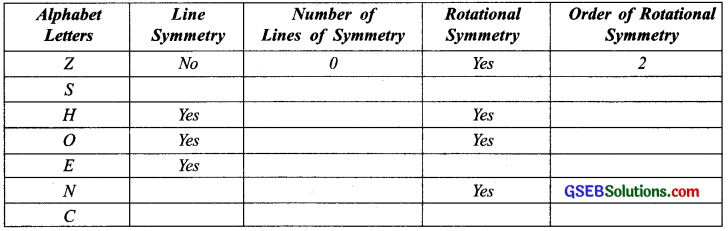
Solution:
