Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.5
![]()
Question 1.
PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
Solution:
In the right APQR, using the Pythagoras property, we have:
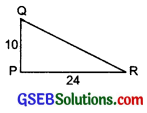
QR² = PR² + PQ²
or QR² = 24² + 10²
or QR² = 576 + 100
or QR² = 676 = 26²
⇒ QR = 26
Thus,QR = 26 cm
Question 2.
ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution:
In the right A, using the Pythagoras property, we have
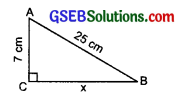
AC² + BC² = AB²
or 7² + x² = 25²
or 49 + x² = 625
or x² = 625 – 49 = 576
or x² = 24²
⇒ x = 24
Thus, BC = 24 cm.
![]()
Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance ‘a’. Find the distance of the foot of the ladder from the wall.
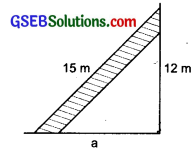
Solution:
The foot of ladder are ‘a’ metres from the wall. Using Pythagoras property, we have
a² + 12² = 15²
or a² + 144 = 225
or a² = 225 – 144 = 81
or a² = 9²
or a = 9m
Hence, the required distance of the foot of the ladder from the wall = 9 m.
Question 4.
Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Solution:
(i) 2.5 cm, 6.5 cm, 6 cm The longest side is 6.5 cm.
Now, (2.5)² + (6)² = 6.25 + 36
= 42.25 = (6.5)²
∴ The given lengths can be the sides of a right triangle.
Obviously, the right angle is the angle between the sides 2.5 cm and 6 cm.
(ii) 2 cm, 2 cm, 5 cm
The longest side is 5 cm.
∴ 2² + 2² = 4 + 4 = 8
But 8 ≠ 5²
∴ The given lengths cannot be the sides of a right triangle.
(iii) 1.5 cm, 2 cm, 2.5 cm The longest side is 2.5 cm
Now (1.5)² + (2)² = 2.25 + 4 = 6.25
Also (2.5)² =6.25
∴ (1.5)² + (2)² = (2.5)²
Thus, the given length can be sides of a right triangle.
Obviously, the right angle is the angle between the sides 1.5 cm and 2 cm.
![]()
Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:
Let the tree BC is broken at the point C, such that CD = CA.
Now, ABC is a right A,
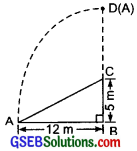
∴ Using the Pythagoras property, we have:
AB² + BC² = AC²
or 12² + 5² = AC²
or 144 + 25 = AC²
or AC² = 169 = 13²
or AC = 13 m
Now, the height of the tree = BD
= BC + CD
= BC + AC
[∵ AC and CD are same]
= 5 m +13 m = 18 m
Thus, the required height of the tree is 18 m.
Question 6.
Angles Q and R of a ∆PQR are 25° and 65°. Write which of the following is true:
(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²
Solution:
In ∆PQR,
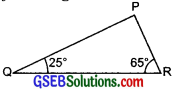
∠P + ∠Q + ∠R = 180°
∴ ∠P + 25° + 65° = 180°
or ∠P + 90° = 180°
or ∠P = 180° – 90° = 90°
So, ∆QPR is a right-angled triangle, having its right angle at P.
Now, Hypotenuse = The side opposite to P = QR
Using the Pythagoras property,
QR² = PQ² + RP²
The relation (ii), i.e. PQ² + RP² = QR² is true.
![]()
Question 7.
Find the perimeter of the .rectangle whose length is 40 cm and a diagonal is 41 cm.
Solution:
Length of the rectangle = 40 cm
Let the breadth be x cm
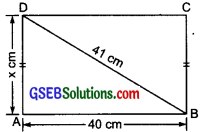
In right ∆BAD, we have
BA² + AD² = BD²
or 40² + x² = 41²
or x² = 41² – 40²
= 1681 – 1600 = 81
or x² = 92 or x = 9
∴ Breadth = 9 cm
Now, Perimeter = 2(length + breadth)
= 2(40 cm + 9 cm)
= 2(49 cm) = 98 cm
Thus, the perimeter of the rectangle is 98 cm.
![]()
Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution:
Let the given figure is a rhombus, such that AC and BD are its diagonal, and AC = 30 cm; BD = 16 cm.
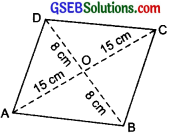
Since, the diagonals of a rhombus bisect each other at right angles (Here they bisect each other at O).
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°.
And, OA= OC = \(\frac { 1 }{ 2 }\)AC = \(\frac { 1 }{ 2 }\) x 30
= 15 cm
And, BO = OD = \(\frac { 1 }{ 2 }\)BD = \(\frac { 1 }{ 2 }\) x 16
= 8 cm
Now, in right-angled ∆AOB, we have
AB² = AO² + BO² = 15² + 8²
= 225 + 64 = 289
or AB² = 17²
or AB = 17 cm
Similarly, in right ABOC,BC =17 cm
in right ∆COD, CD = 17 cm
in right ∆AOD, AD = 17 cm
Now, Perimeter of the rhombus
= AB + BC + CD + AD
= 17 cm + 17 cm + 17 cm + 17 cm
= 68 cm.