GSEB Solutions Class 7 Maths Chapter 6 ત્રિકોણ અને તેના ગુણધર્મો InText Questions

Gujarat Board GSEB Solutions Class 7 Maths Chapter 6 ત્રિકોણ અને તેના ગુણધર્મો InText Questions and Answers.

Gujarat Board Textbook Solutions Class 7 Maths Chapter 6 ત્રિકોણ અને તેના ગુણધર્મો InText Questions

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 113 – 114)

1. ΔABCના છ ઘટકો (એટલે કે 3 બાજુઓ અને 3 ખૂણાઓ) લખો.
ઉત્તરઃ
ΔABCના છ ઘટકો નીચે પ્રમાણે છે :

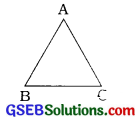
ત્રણ બાજુઓ : \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) અને \(\overline{\mathrm{CA}}\)
ત્રણ ખૂણાઓ: ∠A, ∠B અને ∠C

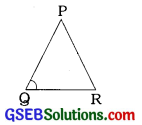
2. (i) ΔPQRમાં શિરોબિંદુ 9ની સામેની બાજુ,
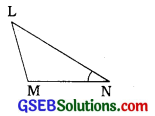
(ii) ΔLMNમાં બાજુ LMની સામેનો ખૂણો,
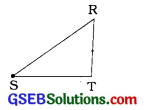
(iii) ΔRSTમાં બાજુ RTની સામેનું શિરોબિંદુ લખો.
ઉત્તરઃ
(i) ΔPQRમાં શિરોબિંદુ Qની સામેની બાજુ \(\overline{\mathrm{PR}}\) છે.

(ii) ΔLMNમાં બાજુ LMની સામેનો ખૂણો ∠N છે.

(iii) ΔRSTમાં બાજુ RTની સામેનું શિરોબિંદુ S છે.

3. નીચેની આકૃતિઓ જુઓ. દરેક ત્રિકોણનું વર્ગીકરણ (i) બાજુઓ પ્રમાણે અને (ii) ખૂણાઓ પ્રમાણે કરોઃ

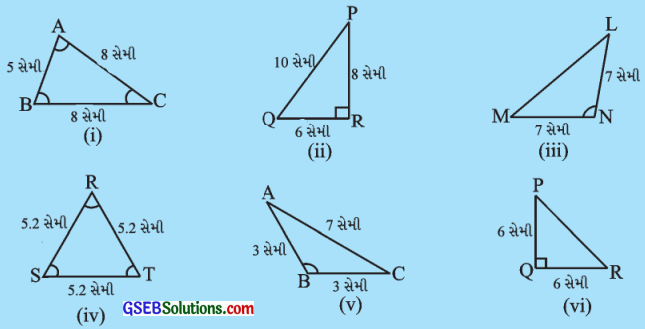
ઉત્તરઃ
(i) અહીં ΔABCમાં AC = BC = 8 સેમી છે.
∴ ΔABC એ સમઢિબાજુ ત્રિકોણ છે.
વળી, ΔABCના ત્રણે ખૂણાનાં માપ 90° કરતાં ઓછા છે.
∴ ΔABC એ લઘુકોણ ત્રિકોણ છે.

(ii) અહીં ΔPQRમાં PQ ≠ QR ≠ RP
∴ ΔPOR એ વિષમબાજુ ત્રિકોણ છે.
વળી, ΔPQRમાં m∠R = 90°
∴ ΔPQR એ કાટકોણ ત્રિકોણ છે.

(iii) અહીં ΔLMNમાં LN = MN = 7 સેમી
∴ ΔLMN એ સમદ્વિબાજુ ત્રિકોણ છે.
વળી, ΔLMNમાં m∠N એ 90° કરતાં વધારે છે.
∴ ΔLMN એ ગુરુકોણ ત્રિકોણ છે.

(iv) અહીં ΔRSTમાં RS = ST = TR = 5.2 સેમી
∴ ΔRST એ સમબાજુ ત્રિકોણ છે.
વળી, ΔRSTમાં ત્રણે ખૂણાનાં માપ 90° કરતાં નાના છે.
∴ ΔRST એ લઘુકોણ ત્રિકોણ છે.

(v) અહીં ΔABCમાં AB = BC = 3 સેમી
∴ ΔABC એ સમદ્વિબાજુ ત્રિકોણ છે.
વળી, ΔABCમાં m∠Bનું માપ 90° કરતાં વધારે છે.
∴ ΔABC એ ગુરુકોણ ત્રિકોણ છે.

(vi) અહીં ΔPQRમાં PQ = QR = 6 સેમી
∴ ΔPQR એ સમઢિબાજુ ત્રિકોણ છે.
વળી, ΔPQRમાં m∠Q = 90°
∴ ΔPQR એ કાટકોણ ત્રિકોણ છે.

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 114)

1. કોઈ પણ ત્રિકોણને કેટલી મધ્યગાઓ હોઈ શકે?
ઉત્તરઃ

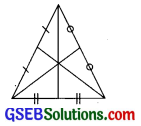
ત્રિકોણને ત્રણ બાજુઓ હોય છે. શિરોબિંદુથી સામેની બાજુના મધ્યબિંદુને જોડતા આવા ત્રણ રેખાખંડ (મધ્યગા) દોરી શકાય.
આમ, ત્રિકોણને ત્રણ મધ્યગાઓ હોય.

2. આખી મધ્યગા ત્રિકોણની અંદરના ભાગમાં સમાયેલી છે? (જો તમને લાગે કે આ સાચું નથી, તો તેવી આકૃતિ દોરીને બતાવો.)
ઉત્તરઃ
હા, આખી મધ્યગા ત્રિકોણની અંદરના ભાગમાં જ સમાયેલી હોય છે.

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 115)

1. એક ત્રિકોણના કેટલા વેધ હોઈ શકે?
ઉત્તરઃ
એક ત્રિકોણને ત્રણ વેધ હોય. ત્રિકોણના શિરોબિંદુથી સામેની બાજુ પર દોરેલો લંબ રેખાખંડ એ ત્રિકોણનો વેધ છે. ત્રિકોણને ત્રણ શિરોબિંદુ હોવાથી ત્રિકોણને ત્રણ વેધ હોય.

2. નીચેના ત્રિકોણો માટે Aમાંથી \(\overline{\mathrm{BC}}\) પરના વેધ દોરોઃ

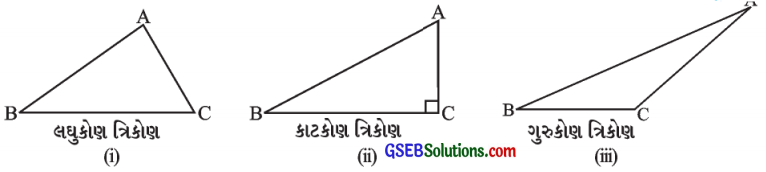
ઉત્તરઃ
નીચે દરેક ત્રિકોણમાં Aમાંથી \(\overline{\mathrm{BC}}\) પર AL વેધ દોય છે :

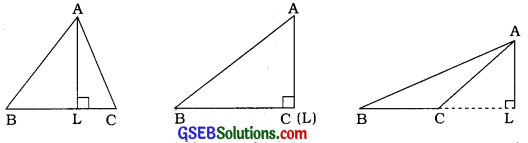
3. શું વેધ હંમેશાં ત્રિકોણની અંદરના ભાગમાં જ આવશે? જો તમને આ સાચું ન લાગતું હોય, તો તે દર્શાવવા કાચી આકૃતિ દોરો.
ઉત્તરઃ

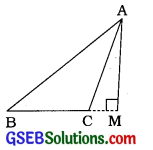
ના, વેધ હંમેશાં ત્રિકોણની અંદરના ભાગમાં જ આવે તેવું નથી. બાજુમાં દર્શાવેલી ગુરુકોણ ત્રિકોણની આકૃતિમાં વેધ \(\overline{\mathrm{AM}}\) એ ΔABCના અંદરના ભાગમાં નથી.

4. તમે એવો ત્રિકોણ વિચારી શકો જેના બે વેધ તેની બે બાજુઓ જ છે?
ઉત્તરઃ

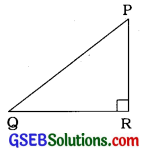
હા, કાટકોણ ત્રિકોણ એ એવો ત્રિકોણ છે જેના બે વેધ તેની બે બાજુઓ જ છે.
અહીં કાટકોણ ત્રિકોણ PQR આપ્યો છે, જેમાં ∠R કાટખૂણો છે, ΔPQRના બે વેધ \(\overline{\mathrm{PR}}\) અને \(\overline{\mathrm{QR}}\) છે જે ΔPQRની બે બાજુઓ જ છે.
જો અન્ય કોઈ ત્રિકોણ રચીએ તો તેના બે વેધ તેની બે બાજુઓ ન હોય.

5. કોઈ ત્રિકોણ માટે વેધ અને મધ્યગા સમાન હોઈ શકે?
ઉત્તરઃ

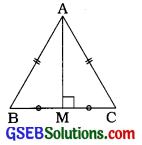
હા, સમબાજુ ત્રિકોણમાં વેધ અને મધ્યગા સમાન હોય છે. અહીં ΔABC એ સમબાજુ ત્રિકોણ છે. અહીં ΔABCનો વેધ \(\overline{\mathrm{AM}}\) એ જ મધ્યગા \(\overline{\mathrm{AM}}\) છે.

વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબર 117)

1. ત્રિકોણના બહિષ્કોણ ઘણી રીતે બનાવી શકાય. તેમાંની ત્રણ રીત નીચે આકૃતિમાં દર્શાવી છે. બહિષ્કોણ મેળવવાની હજુ વધારે ત્રણ રીતો છે. તેની કાચી આકૃતિઓ બનાવવાનો પ્રયત્ન કરો.

ઉત્તરઃ
જુઓ બીજી ત્રણ રીતે ત્રિકોણના બહિષ્કોણ નીચે પ્રમાણે દર્શાવી શકાય:

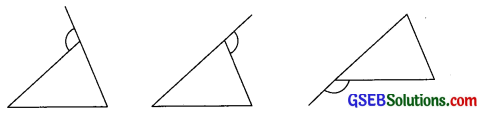
2. ત્રિકોણના દરેક ખૂણા આગળ બનતા બહિષ્કોણ સરખા છે?
ઉત્તરઃ
ના, ત્રિકોણનાં ત્રણે શિરોબિંદુએ બનતા બહિષ્કોણનાં માપ સરખાં ન હોય.

3. ત્રિકોણના બહિષ્કોણ અને તેની અંદરના તેના આસન્નકોણના સરવાળા બાબતે તમે શું કહી શકો?
ઉત્તરઃ
બહિષ્કોણ અને તેનો અંદરનો આસન્નકોણ રેખિક ખૂણાઓની જોડ રચે છે.
∴ બહિષ્કોણનું માપ + અંદરના આસન્નકોણનું માપ = 180°

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 118)

1. જ્યારે બહિષ્કોણ (i) કાટકોણ હોય, (ii) ગુરુકોણ હોય અને (iii) લઘુકોણ હોય, તો દરેક વખતે બંને અંતઃસંમુખકોણ વિશે તમે શું કહી શકો?
ઉત્તરઃ
(i) જ્યારે ત્રિકોણનો બહિષ્કોણ કાટકોણ હોય, ત્યારે બંને અંતઃસંમુખ કોણ એ લઘુકોણ હોય.
(ii) જ્યારે ત્રિકોણનો બહિષ્કોણ ગુરુકોણ હોય, ત્યારે બેમાંથી એક અંત:સંમુખ કોણ લઘુકોણ હોય.
(iii) જ્યારે ત્રિકોણનો બહિષ્કોણ લઘુકોણ હોય, ત્યારે અંદરના બંને અંતઃસંમુખ કોણ લઘુકોણ હોય.

2. કોઈ ત્રિકોણનો બહિષ્કોણ સરળકોણ હોઈ શકે?
ઉત્તરઃ
ના, ત્રિકોણનો બહિષ્કોણ સરળકોણ ન હોઈ શકે.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 118)

1. એક ત્રિકોણના બહિષ્કોણનું માપ 70° છે અને તેના એક અંત સંમુખકોણનું માપ 25° છે. બીજા અંતઃસંમુખકોણનું માપ શોધો.
ઉત્તરઃ

અહીં ત્રિકોણના બહિષ્કોણનું માપ = 70°
ત્રિકોણના બે અંતઃસંમુખકોણનાં માપ 25° અને x છે.
હવે, ત્રિકોણના બે અંતઃસંમુખકોણનો સરવાળો = ત્રિકોણના બહિષ્કોણનું માપ
∴ 25° + ∠x = 70°
∴ ∠x = 70° – 25°
∴ ∠x = 45°
ત્રિકોણના માગેલા અંતઃસંમુખકોણનું માપ 45° છે.

2. એક ત્રિકોણના બહિષ્કોણના અંત સંમુખ કોણોનાં માપ 60° અને 80° છે, તો બહિષ્કોણનું માપ શોધો.
ઉત્તરઃ
ત્રિકોણના બે અંતઃસંમુખકોણનાં માપ 60° અને 80° છે.
હવે, બહિષ્કોણનું માપ = બે અંતઃસંમુખકોણનાં માપનો સરવાળો
= 60° + 80° = 140°
ત્રિકોણના બહિષ્કોણનું માપ 140° છે.

3. બાજુની આકૃતિમાં કંઈ ખોટું છે? તમારું મંતવ્ય લખો.

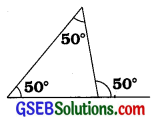
ઉત્તરઃ
કોઈ પણ ત્રિકોણ માટે,
ત્રિકોણના બહિષ્કોણનું માપ = બે અંતઃસંમુખકોણનાં માપનો સરવાળો
અહીં ત્રિકોણના બહિષ્કોણનું માપ = 50°
બે અંતઃસંમુખકોણનાં માપનો સરવાળો = 50° + 50° = 100°
હવે, 50° ≠ 100°
સાચી આકૃતિ માટે ત્રિકોણના બહિષ્કોણનું માપ 100° લખવું જોઈએ.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 122)

1. ત્રિકોણના બે ખૂણા 30° અને 80° છે. ત્રીજો ખૂણો શોધો.
ઉત્તરઃ
ધારો કે ત્રિકોણના ત્રીજા ખૂણાનું માપ x છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.
∴ 30° + 80° + x = 180°
∴ 110° + x = 180°
∴ x = 180° – 110°
∴ x = 70°
ત્રિકોણના ત્રીજા ખૂણાનું માપ 70° છે.

2. ત્રિકોણનો એક ખૂણો 80°નો છે અને બાકીના બંને ખૂણા સરખા છે. તે બંનેનાં માપ શોધો.
ઉત્તરઃ
ધારો કે ત્રિકોણના સરખા ખૂણા પૈકી દરેકનું માપ x છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.
∴ x + x + 80° = 180°
∴ 2x + 80° = 180°
∴ 2x = 180° – 80°
∴ 2x = 100°
∴ \(\frac{2 x}{2}=\frac{100^{\circ}}{2}\)
∴ x = 50°
ત્રિકોણના સરખા ખૂણા પૈકી દરેકનું માપ 50° છે.

3. ત્રિકોણના ત્રણ ખૂણા 1 : 2 : 1ના પ્રમાણમાં છે. આ ત્રિકોણના બધા ખૂણા શોધો. આ ત્રિકોણને બે ભિન્ન રીતે ઓળખો.
ઉત્તરઃ
ત્રિકોણના ત્રણે ખૂણાઓનાં માપ 1 : 2 : 1ના પ્રમાણમાં છે.
ધારો કે આ ત્રિકોણના ત્રણે ખૂણાઓનાં માપ x, 2x અને x છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.
∴ x + 2x + x = 180°
∴ 4x = 180°
∴ \(\frac{4 x}{4}=\frac{180^{\circ}}{4}\)
∴ x = 45° અને 2x = 45° × 2 = 90°
આમ, ત્રિકોણના ત્રણે ખૂણાઓનાં માપ 45°, 90° અને 45° છે.
આ ત્રિકોણના બે ખૂણાઓનાં માપ સરખાં છે તેથી આ ખૂણાઓની સામેની બાજુઓ સરખી થાય. વળી, એક ખૂણાનું માપ 90° છે.
∴ આ ત્રિકોણ સમદ્વિબાજુ ત્રિકોણ પણ છે.
આમ, આ ત્રિકોણ સમદ્વિબાજુ કાટકોણ ત્રિકોણ છે.

વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 122)

1. બે કાટખૂણાવાળો ત્રિકોણ મળી શકે?
ઉત્તરઃ
ના, બે કાટખૂણાવાળો ત્રિકોણ ન મળી શકે.
કારણઃ ત્રિકોણના ત્રણ ખૂણાઓનાં માપનો સરવાળો 180° થાય. હવે, જો ત્રિકોણમાં બે ખૂણા કાટખૂણા હોય, તો આ બે ખૂણાઓનાં માપનો સરવાળો 180° થાય અને ત્રીજા ખૂણાનું માપ તેમાં ઉમેરતાં સરવાળો 180°થી વધી જાય.
આમ, ત્રિકોણ જ શક્ય ન બને.

2. બે ગુરુકોણવાળો ત્રિકોણ મળી શકે?
ઉત્તરઃ
ના, બે ગુરુકોણવાળો ત્રિકોણ ન મળી શકે.
કારણ: ત્રિકોણના ત્રણ ખૂણાઓનાં માપનો સરવાળો 180° થાય છે. હવે, જો ત્રિકોણમાં બે ખૂણા ગુરુકોણ હોય, તો આ બે ખૂણાઓનાં માપનો સરવાળો 180°થી વધી જાય જે ત્રિકોણ માટે શક્ય નથી.

3. બે લઘુકોણવાળો ત્રિકોણ મળી શકે?
ઉત્તરઃ
હા, બે લઘુકોણવાળો ત્રિકોણ મળી શકે.
કારણ : ત્રિકોણના ત્રણ ખૂણાઓનાં માપનો સરવાળો 180° થાય છે. બે ખૂણા લઘુકોણ હોય, અને ત્રીજો ખૂણો લઘુકોણ કે ગુરુકોણ ગમે તે હોવા છતાં ત્રણે ખૂણાનાં માપનો સરવાળો 180° થઈ રહે છે.

4. જેના ત્રણે ખૂણા 60° કરતાં મોટા હોય તેવો ત્રિકોણ મળી શકે?
ઉત્તરઃ
ના, જેના ત્રણે ખૂણા 60° કરતાં મોટા હોય તેવો ત્રિકોણ ન મળી શકે.
કારણ : ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે. જો ત્રિકોણના ત્રણે ખૂણા 60° કરતાં મોટા હોય, તો ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° કરતાં વધી જાય જેથી ત્રિકોણ શક્ય ન બને.

5. જેના ત્રણે ખૂણા 60° હોય તેવો ત્રિકોણ મળી શકે?
ઉત્તરઃ
હા, જેના ત્રણે ખૂણા 60° હોય તેવો ત્રિકોણ મળી શકે.
કારણ : ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે. ત્રિકોણના ત્રણે ખૂણાનાં માપ 60° હોય, તો ત્રિકોણના ત્રણે ખૂણાનાં માપનો સરવાળો 60° + 60° + 60° = 180° થાય. જેથી ત્રિકોણ શક્ય બને છે. આવો ત્રિકોણ સમબાજુ ત્રિકોણ છે.

6. જેના ત્રણે ખૂણા 60° કરતાં નાના હોય તેવો ત્રિકોણ મળી શકે?
ઉત્તરઃ
ના, જેના ત્રણે ખૂણા 60° કરતાં નાના હોય તેવો ત્રિકોણ ન મળી શકે.
કારણ : ત્રિકોણના ત્રણે ખૂણાઓનાં માપન સરવાળો 180° થાય છે. જો ત્રિકોણના ત્રણે ખૂણાઓનાં માપ 60થી નાના હોય, તો આ ત્રણે ખૂણાઓનાં માપનો સરવાળો 180થી ઓછો થાય. જેથી ત્રિકોણ શક્ય ન બને.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 123-124)

1. દરેક આકૃતિમાં ખૂણો x શોધોઃ

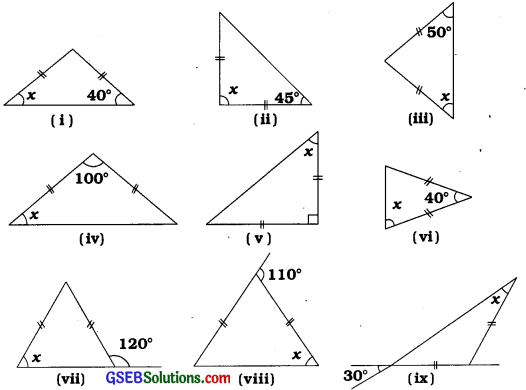
ઉત્તરઃ
(i) આપેલા ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ સરખી બાજુઓની સામેના પાયાના) બંને ખૂણાનાં માપ સરખાં હોય. પાયાના એક ખૂણાનું માપ 40° છે.
∴ ∠x = 40°

(ii) આપેલા ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ સરખી બાજુઓની સામેના બંને ખૂણાનાં માપ સરખાં હોય.
∴ શિરોબિંદુ આગળના ખૂણાનું માપ 45° છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય.
∴ ∠45° + ∠45° + x = 180°
∴ 90° + x° = 180°
∴ x° = 180° – 90°
∴ ∠x = 90°

(iii) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
∴ ∠x = 50°

(iv) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
∴ ત્રિકોણમાં બાકીના એક પાયાના ખૂણાનું માપ x છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય.
∴ ∠x + ∠x + 100° = 180°
∴ 2∠x + 100° = 180°
∴ 2∠x = 180° – 100°
∴ 2∠x = 80°
∴ \(\frac{2 \angle x}{2}=\frac{80^{\circ}}{2}\)
∴ ∠x = 40°

(v) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
∴ ત્રિકોણમાં શિરોબિંદુના ખૂણાનું માપ x છે. તેથી પાયાના ખૂણાનું માપ x છે.
વળી, આ ત્રિકોણ કાટકોણ ત્રિકોણ પણ છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય.
∴ ∠x + ∠x + 90° = 180°
∴ 2∠x + 90° = 180°
∴ 2∠x = 180° – 90°
∴ 2∠x = 90°
∴ \(\frac{2 \angle x}{2}=\frac{90^{\circ}}{2}\)
∴ ∠x = 45

(vi) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
∴ ત્રિકોણમાં એક ખૂણાનું માપ x પણ છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય.
∴ ∠x + ∠x + 40° = 180°
∴ 2∠x + 40° = 180°
∴ 2∠x = 180° – 40°
∴ 2∠x = 140°
∴ \(\frac{2 \angle x}{2}=\frac{140^{\circ}}{2}\)
∴ ∠x = 70°

(vii) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
∴ ત્રિકોણમાં પાયાના બીજા ખૂણાનું માપ x છે.
હવે, ∠x અને 120° એ રેખિક જોડના ખૂણા છે.
∴ ∠x + 120° = 180°
∴ ∠x = 180° – 120°
∴ ∠x = 60°

(viii) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
પાયાના એક ખૂણાનું માપ x છે. તેથી પાયાના બીજા ખૂણાનું માપ x છે.
હવે, ત્રિકોણના બહિષ્કોણનું માપ = અંતઃસંમુખ બે ખૂણાઓનાં માપનો સરવાળો
∴ ∠x + ∠x = 110°
∴ 2∠x = 110°
∴ \(\frac{2 \angle x}{2}=\frac{110^{\circ}}{2}\)
∴ ∠x = 55°

(ix) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
∴ ત્રિકોણનો પાયાનો એક ખૂણો પણ x હોય.
હવે, ∠x અને 30° અભિકોણો છે.
∴ ∠x = 30°

2. દરેક આકૃતિમાં ખૂણા x અને પુ શોધોઃ

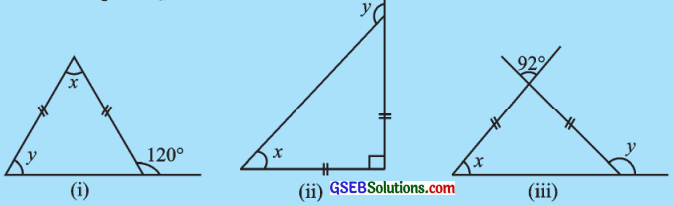
ઉત્તરઃ
(i) આકૃતિમાં ત્રિકોણની બે બાજુઓનાં માપ સરખાં છે.
∴ સરખી બાજુઓની સામેના ખૂણાઓનાં માપ સરખાં હોય.
હવે, પાયાના એક ખૂણાનું માપ છે.
∴ પાયાના બીજા ખૂણાનું માપ પણ છે.
હવે, ∠y અને 120° એ રેખિક જોડના ખૂણા છે.
∴ ∠y + 120° = 180°
∴ ∠y = 180° – 120°
∴ ∠y = 60°
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.’
∴ ∠x + ∠y + ∠y = 180°
∴ ∠x + 60° + 60° = 180°
∴ ∠x + 120° = 180°
∴ ∠x = 180° – 120°
∴ ∠x = 60°
આમ, ∠x = 60° અને ∠y = 60°

(ii) આપેલ ત્રિકોણ કાટકોણ ત્રિકોણ છે તેથી તેના એક ખૂણાનું માપ 90° છે.
ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ ત્રિકોણમાં સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
ત્રિકોણમાં પાયાના એક ખૂણાનું માપ x છે. તેથી શિરકોણનું માપ x છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.
∴ ∠x + ∠x + 90° = 180°
∴ 2∠x + 90° = 180°
∴ 2∠x = 180° – 90°
∴ 2∠x = 90°
∴ \(\frac{2 \angle x}{2}=\frac{90^{\circ}}{2}\)
∴ ∠x = 45°
હવે, ત્રિકોણનો બહિષ્કોણનું માપ = ત્રિકોણના બે અંતઃસંમુખ કોણોનો સરવાળો
∴ ∠y = 45° + 90° = 135°
આમ, ∠x = 45° અને ∠y = 135°

(iii) ત્રિકોણમાં બે બાજુઓનાં માપ સરખાં છે.
∴ સરખી બાજુઓની સામેના ખૂણાનાં માપ સરખાં હોય.
ત્રિકોણમાં પાયાનો એક ખૂણો x છે. તેથી બીજો પાયાનો ખૂણો x હોય.
ત્રિકોણમાં શિરકોણ અને 92° અભિકોણ છે.
∴ આ ત્રિકોણનો શિર કોણ 92° છે.
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય છે.
∴ ∠x + ∠x + 92° = 180°
∴ 2∠x + 92° = 180°
∴ 2∠x = 180° – 92°
∴ 2∠x = 88°
∴ \(\frac{2 \angle x}{2}=\frac{88^{\circ}}{2}\)
∴ ∠x = 44°
હવે, ∠x અને ∠y રૈખિક જોડના ખૂણા છે.
∴ ∠x + ∠y = 180°
∴ 44° + ∠y = 180°
∴ ∠y = 180° – 44°
∴ ∠y = 136°
આમ, ∠x = 44° અને ∠y = 136°

વિચારો, ચર્ચા કરો અને લખો: (પાઠ્યપુસ્તક પાન નંબર 127)

શું ત્રિકોણના કોઈ પણ બે ખૂણાઓનાં માપનો સરવાળો એ હંમેશાં ત્રીજા ખૂણાના માપ કરતાં વધુ હોય છે?
ઉત્તરઃ
ના, ત્રિકોણના કોઈ પણ બે ખૂણાઓનાં માપનો સરવાળો એ ત્રીજા ખૂણાના માપ કરતાં વધારે હોય અથવા ન પણ હોય.

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 129-130)

નિચેની આકૃતિઓમાં અજ્ઞાત લંબાઈ x શોધોઃ


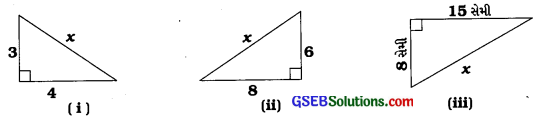
ઉત્તરઃ
(i) અહીં આપેલા કાટકોણ ત્રિકોણમાં અજ્ઞાત બાજુ x એ કર્ણ છે.
∴ (કર્ણ)² = (એક બાજુ)² + (બીજી બાજુ)²
∴ x² = (3)² + (4)²
∴ x² = 9 + 16
∴ x² = 25
∴ x² = 5²
∴ x = 5

(ii) અહીં આપેલા કાટકોણ ત્રિકોણમાં અજ્ઞાત બાજુ x એ કર્ણ છે.
∴ (કર્ણ)² = (એક બાજુ)² + (બીજી બાજુ)²
∴ x² = 6² + 8²
∴ x² = 36 + 64
∴ x² = 100
∴ x² = 10²
∴ x = 10

(iii) અહીં આપેલા કાટકોણ ત્રિકોણમાં અજ્ઞાત બાજુ x એ કર્ણ છે.
∴ (કર્ણ)² = (એક બાજુ)² + (બીજી બાજુ)²
∴ x² = 8² + 15²
∴ x = 64 + 225
∴ x² = 289
∴ x² = 17²
∴ x = 17

(iv) અહીં આપેલા કાટકોણ ત્રિકોણમાં અજ્ઞાત બાજુ x એ કર્ણ છે. તે
∴ (કર્ણ)² = (એક બાજુ)² + (બીજી બાજુ)²
∴ x² = 7² + 24²
∴ x² = 49 + 576
∴ x² = 625
∴ x² = 25²
∴ x = 25

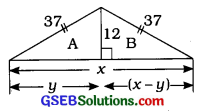
(v) ત્રિકોણ A માટે
y² + 12² = 37²
∴ y² + 144 = 1369
∴ y² = 1369 – 144
∴ y² = 1225
∴ y² = 35²
∴ y = 35

ત્રિકોણ B માટે
(x – y)² + 12² = 37²
∴ (x – y)² + 144 = 1369
∴ (x – y)² = 1369 – 144
∴ (x – y)² = 1225
∴ (x – y)² = 35²
∴ x – y = 35
∴ x – 35 = 35
∴ x = 35 + 35 = 70

(vi) અહીં આપેલા કાટકોણ ત્રિકોણમાં અજ્ઞાત બાજુ x એ કર્ણ છે.
∴ (કર્ણ)² = (એક બાજુ)² + (બીજી બાજુ)²
∴ x² = (12)² + (5)²
∴ x² = 144 + 25
∴ x² = 169
∴ x² = 13²
∴ x = 13
નોંધઃ આ આકૃતિમાં પાયા ઉપરના વેધની લંબાઈ ધ્યાનમાં લેતા નથી.

વિચારો, ચર્ચા કરો અને લખો (પાન નંબર 131)

1. P આગળ કાટખૂણો હોય તેવા ΔPQRની લાંબામાં લાંબી બાજુ કઈ?
ઉત્તરઃ

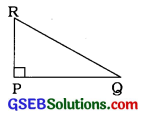
ΔPQRમાં ∠P કાટખૂણો છે.
∴ ∠Pની સામેની બાજુ \(\overline{\mathrm{RQ}}\) એ કર્ણ છે.
કાટકોણ ત્રિકોણમાં કર્ણ જ સૌથી લાંબામાં લાંબી બાજુ હોય.
ΔPQRની સૌથી લાંબામાં લાંબી બાજુ \(\overline{\mathrm{RQ}}\) છે.

2. B આગળ કાટખૂણો હોય તેવા ΔABCની લાંબામાં લાંબી બાજુ કઈ?
ઉત્તરઃ

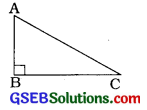
ΔABCમાં ∠B કાટખૂણો છે.
∴ ∠Bની સામેની બાજુ \(\overline{\mathrm{AC}}\) એ કર્ણ છે.
કાટકોણ ત્રિકોણમાં કર્ણ જ સૌથી લાંબામાં લાંબી બાજુ હોય.
∴ ΔABCની સૌથી લાંબામાં લાંબી બાજુ \(\overline{\mathrm{AC}}\) છે.

3. કાટકોણ ત્રિકોણની લાંબામાં લાંબી બાજુ કઈ?
ઉત્તરઃ
કાટકોણ ત્રિકોણમાં કર્ણ જ સૌથી લાંબામાં લાંબી બાજુ છે.

4. “લંબચોરસના વિકર્ણ પર દોરેલા ચોરસનું ક્ષેત્રફળ, તેની લંબાઈ અને પહોળાઈ પર દોરેલા ચોરસનાં ક્ષેત્રફળના સરવાળા જેટલું થાય છે.” આ બૌધાયનનું પ્રમેય છે. આને પાયથાગોરસના પ્રમેય સાથે સરખાવો.
ઉત્તરઃ

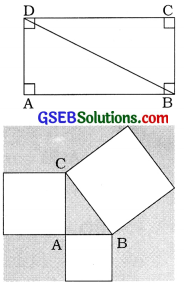
અહીં લંબચોરસ ABCD આપ્યો છે.
જેમાં \(\overline{\mathrm{BD}}\) તેનો વિકર્ણ છે.
બોધાયન પ્રમેય પરથી,
(વિકર્ણ)² = (લંબાઈ)² + (પહોળાઈ)²
∴ (BD)² = (AB)² + (AD)² … (1)
હવે, ΔABC એ કાટકોણ ત્રિકોણ છે.
જેમાં ∠A કાટખૂણો છે.
∴ (કર્ણ)² = (એક બાજુ)² + (બીજી બાજુ)²
∴ (BC)² = (AB)² + (AC)² … (2)
પરિણામ (1) અને (2) પરથી જણાય છે કે બોધાયન પ્રમેય અને પાયથાગોરસ પ્રમેય એક જ છે.