GSEB Solutions Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.2

Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.2

Question 1.
Which congruence criterion do you use in the following?
(a) Given:
AC = DF
AB = DE
BC = EF
So, ∆ABC ≅ ∆DEF

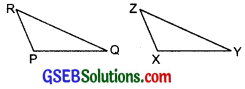
(b) Given:
ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR = ∆XYZ

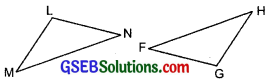
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ∆LMN ≅ ∆GFH

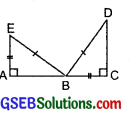
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ∆ABE ≅ ∆CDB

Solution:
(a) SSS congruence criterion
(b) SAS congruence criterion
(c) ASA congruence criterion
(d) RHS congruence criterion

Question 2.
You want to show that ∆ART ≅ ∆PEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =

(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have

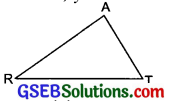
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have P

(i) ∠ATR =
(ii) ∠TAR =
Solution:
Here ∆ART ≅ ∆PEN
∴ A ↔ P, R ↔ E and T ↔ N

(a) (i) AR = PE
(ii) RT = EN
(iii) AT = PN

(b) ∵ ∠T = ∠N
(i) RT = EN
(ii) PN = AT

(c) (i) ∠ATR = ∠PNE
(ii) ∠TAR = ∠NPE

Question 3.
You have to show that ∆AMP ≅ ∆AMQ. In the following proof, supply the missing reasons.

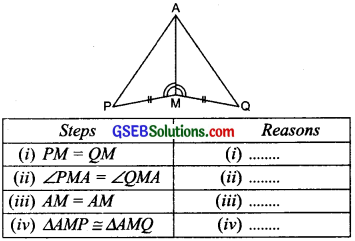
Solution:

Question 4.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°. In ∆PQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°. A student says that ∆ABC ≅ APQR by AAA congruence criterion. Is he justified? Why or why not?
Solution:
No, he is not justified.
Because AAA is not a congruence criterion.

Question 5.
In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ∆RAT ≅?

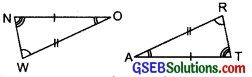
Solution:
We have \(\left.\begin{array}{l}
\mathrm{O} \leftrightarrow \mathrm{A} \\
\mathrm{N} \leftrightarrow \mathrm{T} \\
\mathrm{W} \leftrightarrow \mathrm{R}
\end{array}\right\}\) ⇒ ∆RAT ≅ ∆WON

Question 6.
Complete the congruence statement:

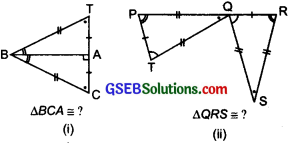
Solution:
(i) We have:
\(\left.\begin{array}{l}
A \leftrightarrow A \\
B \leftrightarrow B \\
T \leftrightarrow C
\end{array}\right\} \Rightarrow \Delta B C A \cong \Delta B T A\)

(ii) \(\left.\begin{array}{l}
R \leftrightarrow P \\
Q \leftrightarrow T \\
S \leftrightarrow Q
\end{array}\right\} \Rightarrow \Delta Q R S \cong \Delta T P Q\)

Question 7.
In a squared sheet, draw two triangles of equal areas such that
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Solution:

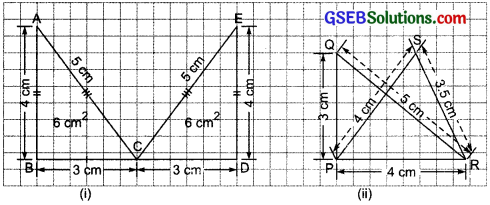
(i) Area of ∆ABC = \(\frac { 1 }{ 2 }\) x 4 x 3 = 6 sq. cm
Area of ∆CDE = \(\frac { 1 }{ 2 }\) x 4 x 3 = 6 sq. cm
Perimeter of ∆ABC = (3 + 4 + 5) cm = 12 cm
Perimeter of ∆CDE = (3 + 4 + 5) cm = 12 cm
The two triangles are congruent.
[Perimeter of ∆ABC] = [Perimeter of ∆CDE]

(ii) Area of ∆PQR = Area of ∆PRS
Perimeter of ∆PQR = (3 + 4 + 5) cm = 12 cm
Perimeter of ∆PRS = (4 + 3.5 + 4) cm = 1.5 cm
The two triangles are not congruent.
[Perimeter of ∆PQR] ≠ [Perimeter of ∆PRS]

Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Solution:
A pair of triangle with 3 equal angles and two equal sides are non-congruent are as follows:

∆ABC and ∆DEF are not congruent as any two sides and angle included between these two sides of ∆ABC is not equal to the corresponding two sides and included angle of ∆DEF.

Question 9.
If ∆ABC and ∆PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

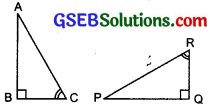
Solution:
Here ∆ABC ≅ ∆PQR
∴ A ↔ P, B ↔ Q and C ↔ R
Two angles ∠B and ∠C of ∆ABC are respectively equal to two angles ∠Q and ∠R of ∆PQR.
∴ BC = QR
We use the ASA congruence criterion

Question 10.
Explain, why ∆ABC ≅ ∆FED.

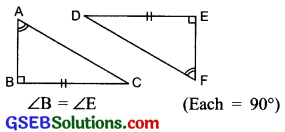
Solution:
∵ ∠A = ∠F (Given)
∴ ∠C = ∠D (Third angles are equal)
Also, BC = ED (Given)
Two angles (∠B and ∠C) and included side BC of ∆ABC are respectively equal to two angles (∠E and ∠D) and the included side ED of
∴ ∆ABC ≅ ∆FED.