Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 7 Congruence of Triangles InText Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 7 Congruence of Triangles InText Questions
![]()
Think, Discuss and Write (Page 137)
Question 1.
When two triangles, say ABC and PQR are given, there are, in all, six possible matchings or correspondences. Two of them are:
(i) ABC ↔ PQR
(ii) ABC ↔ QRP
Find the other four correspondences by using two cutouts of triangles. Will all these correspondences lead to congruence? Think about it.
Solution:
The other 4 correspondences are:
(i) ABC ↔ PRQ
(ii) ABC ↔ QPR
(iii) ABC ↔ RPQ
(iv) ABC ↔ RQP
Yes, all these correspondences may lead to congruence.
Try These (Page 140)
Question 1.
In the following figures, lengths of the sides of the triangles are indicated. By applying the SSS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form:
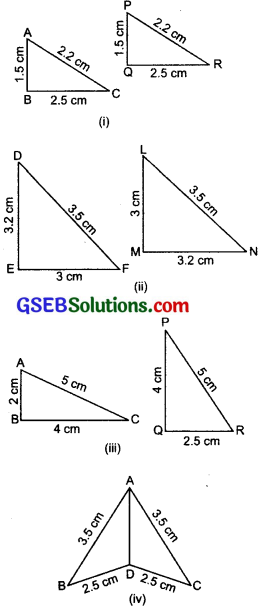
Solution:
(i) We have ∆ABC and ∆PQR, such that

Because the three sides of ∆ABC are equal to the three sides of ∆PQR, therefore the two triangles are congruent. [By SSS congruency rule] Now from the above equality relations, we have A ↔ P, B ↔ Q, C ↔
∴ ∆ABC ≅ ∆PQR
(ii) We have ∆DEF and ∆LMN, such that

i.e. the three sides of ADEF are equal to three sides of ALMN. So, by SSS congruency rule, the two triangles are congruent. From the above equality relations, we have
D ↔ N, E ↔ M and F ↔ L
∴ ∆DEF ≅ ∆NML
(iii) We have ∆ABC and ∆PQR, such that

Since AB ≠ QR, therefore ∆ABC and ∆PQR are not congruent.
(iv) We have ∆ABD and ∆ADC, such that AB = 3.5cm
Since, three sides of ∆ABD are equal to the three sides of ∆ACD, therefore the two triangles are congruent.
From the above equality relations, we have
A ↔ A, B ↔ C and D ↔ D
∴ ∆ABD ≅ AACD
![]()
Question 2.
In the adjoining figure, AB = AC and D is the mid-point of \(\overline{B C}\)
(i) State the three pairs of equal parts in ∆ADB and ∆ADC.
(ii) Is ∆ADB ≅ ∆ADC? Give reasons.
(iii) Is ∠B = ∠C? Why?
Solution:
Here, AB = AC and D is the mid-point \(\overline{B C}\).
i.e. BD = DC
(i) We have; ∆ADB and ∆ADC, such that
AB = AC (Given)
AD = AD (Common)
BD = DC
(∵ D is the mid-point of BC)
(ii) ∵ The three sides of ∆ADB are equal to the three sides of ∆ADC. Therefore, by SSS rule of congruency, the two triangles are congruent.
From the above equality relations, we have
A ↔ A, D ↔ D, B ↔ C
∴ ∆ADB ≅ ∆ADC
(iii) ∵ ∆ADB ≅ ∆ADC
∴ Their corresponding parts are equal, i.e.
B ↔ C
or ∠B = ∠C
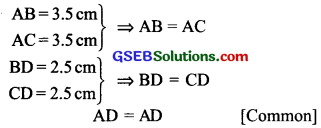
Question 3.
In the adjoining figure, AC = BD and AD = BC. Which of the following statements is meaningfully written?
(i) ∆ABC ≅ ∆ABD
(ii) ∆ABC ≅ ABAD
Solution:
Here, AC BD and AD = BC.
In the given triangles, we have
AB = AB [Common]
BD = AC [Given]
AD = BC [Given]
i.e. the three sides of ∆ABD are equal to the three sides of ∆ABC. So, the two traingles are congruent. From the above equality relations, we have A B, B A, D C
∴ (i) ∆ABC ≅ ∆ABD is not true or meaningless.
(ii) ∆ABC ≅ ∆BAD is true of meaningful.
![]()
Think, Discuss and Write (Page 141)
Question 1.
ABC is an isosceles triangle with AB = AC. Take a trace-copy of ∆ABC and also name it as ∆ABC.
(i) State the three pairs of equal parts in ∆ABC and ∆ACB.
(ii) Is ∆ABC ≅ ∆ACB? Why or why not?
(iii) Is ∠B = ∠C Why or why not?
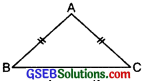
Solution: We have ∆ABC is an isosceles triangle with
AB = AC.
(i) Now, in ∆ABC and ∆ACB,
BC = BC [Common]
AB = AC [Given]
AC = AB [Construction]
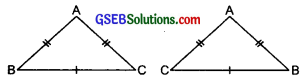
(ii) Yes, all the three sides of ∆ABC are equal to the three sides of ∆ACB and A ↔ A,B ↔ C and C ↔ B.
(iii) Yes
∵ B ↔ C
∴ ∠B = ∠C.
Try These (Page 143)
Question 1.
Which angle is included between the sides \(\overline{D E}\) and \(\overline{E F}\) is ∆DEF.
Solution:
In ∆DEF, the angle between \(\overline{D E}\) and \(\overline{E F}\) is ∠DEF.
Question 2.
By applying SAS congruence rule, you want to establish that ∆PQR ≅ ∆FED. It is given that PQ = FE and RP = DF. What additional informaHon is needed to establish the congruence?
Solution:
We have ∆PQR ≅ ∆FED
[Using SAS congruence rule]
∴ P ↔ F, Q ↔ E, R ↔ D
and PQ = FE and RP = DF.
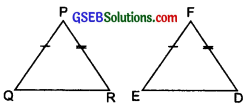
Since in SAS congruence rule, included angle between PQ and RP is equal to the included angle between EF and DF. i.e. ∠P = ∠F
![]()
Question 3.
In the following figures, measures of some parts of the triangles are indicated. By applying SAS congruence rule, state the pairs of congruent triangles, if any, in each case. In case of congruent triangles, write them in symbolic form.
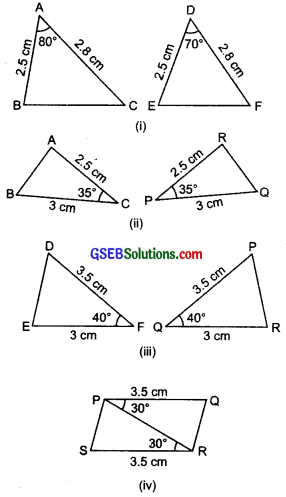
Solution:
(i) ∆ABC and ∆DEF:

∴ ∆ABC and ∆DEF are not congruent.
(ii) ∆ABC and ∆PQR:

∵ Two sides of ∆ABC and their included angle are equal to the two corresponding sides and their included angle of ∆PQR. Therefore, the two triangles are congruent.
Also, we have C ↔ P, A ↔ R and B ↔ Q
∴ ∆ABC ≅ ∆RQP
(iii) ∆DEF and ∆PQR

∵ Two sides of ∆DEF and their included angle are equal to two corresponding sides and their included angle of ∆PQR.
∴ The two triangles are congruent by SAS congruence rule.
Also, F ↔ Q, D ↔ P, and E ↔ R
∴ ∆DEF ≅ ∆PRQ
∆PRS ≅ ∆QPR
(iv) \(\left.\begin{array}{l}
P Q=3.5 \mathrm{~cm} \\
S R=3.5 \mathrm{~cm}
\end{array}\right\}\)
PR = PR [common] ⇒ PQ = SR
\(\left.\begin{array}{l}
\text { Included } \angle \mathrm{QPR}=30^{\circ} \\
\text { Included } \angle \mathrm{PRS}=30^{\circ}
\end{array}\right\}\) ⇒ Included ∠QPR
= ∠PRS
i.e. two sides of ∆PQR and their included angle are equal to two corresponding sides and their included angle of ∆PRS.
∴ Using SAS congruence rule, the two triangles are congruent.
Now, P ↔ R, Q ↔ S.
∴ ∆PQR ≅ ∆RSP
![]()
Question 4.
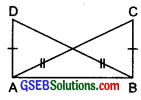
In the adjoining figure, \(\overline{A B}\) and \(\overline{C D}\) bisect each other at O.
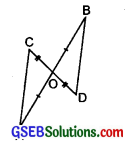
(i) State the three pairs of equal parts in two triangles AOC and BOD.
(ii) Which of the following statements A are true?
(a) ∆AOC ≅ ∆DOB
(b) ∆AOC ≅ ∆BOD
Solution:
Since \(\overline{A B}\) and \(\overline{C D}\) bisect each other at O.
∴ AO = BO amd CO = DO
Also, vertically opposite angles ∠AOC = ∠BOD
(i) ∆AOC and ∆BOD:
We have AO = BO and CO = DO
∠AOC = ∠BOD
(ii) From above equality relations, we have two sides and their included angle of ∆AOC are equal to two corresponding sides and their included angle of ∆BOD.
∴ By SAS congruence rule, the two triangles are congruent.
Also, O ↔ O, A ↔ B, C ↔ D
∴ ∆AOC ≅ ∆BOD
(a) The statement ∆AOC ≅ ∆DOB is false.
(b) The statement ∆AOC ≅ ∆BOD is true.
Try These (Page 145)
Question 1.
What is the side included between the angles M and N of ∆MNP
Solution:
In ∆MNP, the side included between M and N is \(\overline{M N}\).
![]()
Question 2.
You want to establish ∆DEF ≅ ∆MNP, using the ASA congruence rule. You are given that ∠D = ∠M and ∠F = ∠P. What information is needed to establish the congruence? (Draw a rough figure and then try!)
Solution:
To establish ∆DEF ≅ ∆MNP, using ASA congruence rule, we need the side containing ∠D and ∠F to be equal to the side containing ∠M and ∠P.
i.e. We need \(\overline{D F}\) = \(\overline{M P}\)
Question 3.
In the following figures, measures of some parts are indicated. By applying ASA congruence rule, state which pairs of triangles are congruent. In case of congruence, write the result in symbolic form.
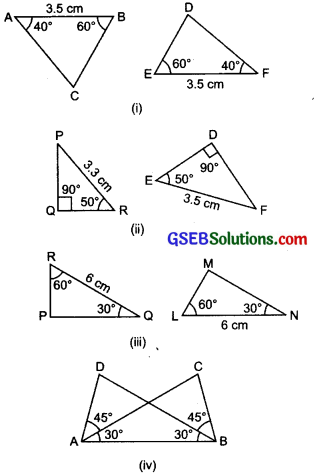
Solution:
(i) ∆ABC and ∆DEF:
We have
\(\left.\begin{array}{l}
A B=3.5 \mathrm{~cm} \\
E F=3.5 \mathrm{~cm}
\end{array}\right\}\) ⇒ AB = FE
\(\left.\begin{array}{l}
\angle \mathrm{A}=40^{\circ} \\
\angle \mathrm{F}=40^{\circ}
\end{array}\right\} \Rightarrow \angle \mathrm{A}\) = ∠F
\(\left.\begin{array}{l}
\angle \mathrm{B}=60^{\circ} \\
\angle \mathrm{E}=60^{\circ}
\end{array}\right\} \Rightarrow \angle \mathrm{B}\) = ∠E
∴ The two triangles are congruent (using the ASA congruence rule).
∵ A ↔ F, B ↔ E and C ↔ D
∆ABC ≅ ∆FED
(ii) ∆PQR and ∆DEF:
In ∆PQR, ∠P = ∠180° – (90° + 50°)
= 40°
Also in ∆DEF, ∠F = 180° – 90° – 50°
= 40°
Now in ∆PQR and ∆DEF, we have
\(\left.\begin{array}{l}
P R=3.3 \mathrm{~cm} \\
E F=3.5 \mathrm{~cm}
\end{array}\right\} \Rightarrow \mathrm{PR} \neq \mathrm{EF}\)
\angle \mathrm{R}=50^{\circ} \\
\angle \mathrm{E}=50^{\circ}
\end{array}\right\} \Rightarrow \angle \mathrm{R}=\angle \mathrm{E}\) \(\left.\begin{array}{l}
\angle \mathrm{P}=40^{\circ} \\
\angle \mathrm{F}=40^{\circ}
\end{array}\right\} \Rightarrow \angle \mathrm{P}=\angle \mathrm{F}\)
∴ Using the ASA congruence rule, we can say that the two triangles are not congruent.
(iii) ∆PQR and ∆LMN:
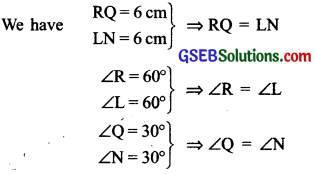
Therefore, using ASA congruence rule, the two triangles are congruent.
Now, R ↔ L,Q ↔ N and P ↔ M
∴ ∆PQR ≅ ∆MNL
(iv) AABC and AABD:
We have AB = AB [Common]
\(\left.\begin{array}{l}
\angle \mathrm{BAD}=45^{\circ}+30^{\circ}=75^{\circ} \\
\angle \mathrm{ABC}=45^{\circ}+30^{\circ}=75^{\circ}
\end{array}\right\}\)
⇒ ∠BAD = ∠ABC
∴ Using ASA congruence rule, we say that two triangles are congruent.
Now, A ↔ B, D ↔ C.
∴ ∆ABC ≅ ∆BAD
![]()
Question 4.
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by ASA congruence rule. In case of congruence, write it in symbolic form.
∆DEF
(i) ∠D = 60°, ∠F = 80°, ∠F = 5 cm
(ii) ∠D = 60°, ∠F = 80°, ∠F = 6 cm
(iii) ∠F = 80°, ∠F = 30°, ∠F = 5 cm
∆PQR
(i) ∠Q = 60°, ∠R = 80°, ∠R = 5 cm
(ii) ∠Q = 60°, ∠R = 80°, ∠P = 6 cm
(iii) ∠P = 80°, ∠Q = 5 cm, ∠R = 30°
Solution:
(i) ∵ ∠D = ∠Q (each = 60°)
∠F = ∠R (each = 80°)
Included side DF = Included side QR [each = 5 cm]
∴ Using ASA congruence rule, we can say that two triangles are congruent.
Also, D ↔ Q, F ↔ R and E ↔ P
∴ ∆DEF ≅ ∆QPR
(ii) Here, QP is not the included side.
∴ The given triangles are not congruent.
(iii) Here, PQ is not the included side.
∴ The given triangles are not congruent.
Question 5.
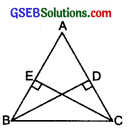
In the adjoining figure, ray AZ bisects ∠DAB as well as ∠DCB.
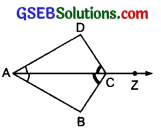
(i) State the three pairs of equal parts in triangles BAC and DAC.
(ii) Is ∆BAC ≅ ∆DAC? Give reasons.
(iii) Is AB = AD? Justify your answer.
(iv) Is CD = CB? Give reasons.
Solution:
(i) ∵ AC is the bisector of ∠DAB, as well as of ∠DCB
∠DAC = ∠BAC and ∠DCA = ∠BCA
Now, in ∠BAC and ∠DAC, equal parts are:
AC = AC [Common]
∠DAC = ∠BAC [AC is a bisector]
∠DCA = ∠BCA [AC is a bisector]
(ii) From the above equality relation, the two triangles are congruent (using ASA congruence rule).
Also, A ↔ A, C ↔ C and D ↔ B
∴ ∆ADC ≅ ∆ABC
or ∆BAC ≅ ∆DAC
(iii) ∵ ∆BAC ≅ ∆DAC
∴ The corresponding parts are equal,
i.e. AB = AD
(iv) ∵ C ↔ C and D ↔ B
∴ CD = CB
or we have ∆BAC ≅ ∆ADAC
∴ The corresponding parts are equal,
i.e. CD = CB.
![]()
Try These (Page 148)
Question 1.
In the following figures, measures of some parts of triangles are given. By applying RHS congruence rule, state which pairs of triangles are congruent. In case of congruent triangles, write the result in symbolic form.
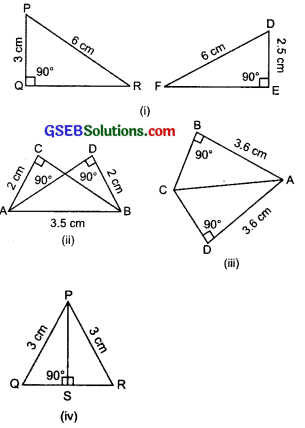
Solution:
(i) Right ∆PQR and Right ∆DEF:
We have two right triangles PQR and DEF, such that:
Hypotenuse PR = Hypotenuse DF [each 6 cm]
But side PQ (3 cm) ≠ DE (2.5 cm)
∴ ∆PQR is not congruent to ∆DEF.
(ii) Right ∆ABC and Right ∆ABD:
We have two right triangles ABC and ABD, such that:
Hypotenuse AB = Hypotenuse BA [Common]
Side AC = Side BD [each = 2 cm]
So, using RHS congruence rule, we can say that the two right triangles are congruent.
Now, A ↔ B, B ↔ A, C ↔ D
∴ ∆ABC ≅ ∆BAD
(iii) Right AABC and Right ∆ACD:
We have right ∆ABC and right ∆ACD, such that: Hypotenuse AC = Hypotenuse AC [Common]
Side \(\overline{A B}\) = Side \(\overline{A D}\) [Each = 3.6 cm]
∴ The two right triangles are congruent.
Now, A ↔ A, C ↔ C, B ↔ D
∴ ∆ABC ≅ ∆ADC
(iv) Right ∆PQS and Right ∆PRS:
We have right ∆PQS and right ∆PRS, such that: Hypotenuse PQ Hypotenuse PR [each = 3 cm] Side PS = Side PS [Common]
∴ Using RHS congruence rule, the two right triangles are congruent.
Now, P ↔ P, S ↔ S, Q ↔ R
∴ ∆PQS ≅ ∆PRS
![]()
Question 2.
It is to be established by RHS congruence rule that ∆ABC = ∆RPQ. What additional information is needed, if it is given that ∠B = ∠P = 90° and AB = RP?
Solution:
We have ∆ABC ≅ ∆RPQ
Since, ∠B = 90° ⇒ Side AC is hypotenuse
and ∠P = 90° ⇒ Side RQ is hypotenuse
∵ AB = RP
∴ The required information needed is Hypotenuse AC = Hypotenuse RQ.
Question 3.
In the adjoining figure, BD and CE are altitudes of ∆ABC such that BD = CE.
(i) State the three pairs of equal parts in ∆CBD and ∆BCE.
(ii) Is ∆CBD = ∆BCE? Why or why not?
(iii) Is ∆DCB = ∆EBC Why or why not?
Solution:
(i) Hypotenuse BC = Hypotenuse BC
[Common]
Side BD = Side CE [Given]
∠BEC = ∠BDC = 90°
The above equality pairs are the required three equal parts in ∆CBD and ∆BCE.
(ii) ∵ ∠D = ∠E and ∠B ↔ ∠C
∴ ∆ CBD ≅ ∆BCE
(iii) ∵ ∆CBD ≅ ABCE
∴ Their corresponding parts are equal.
or ∠DCB = ∠EBC.
![]()
Question 4.
ABC is an isosceles triangle with AB = AC and AD is one of its altitudes.
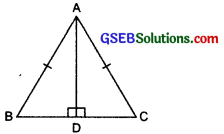
(i) State the three pairs of equal parts in ∆ADB and ∆ADC.
(ii) Is ∆ADB = ∆ADC? Why or why not?
(iii) Is ∠B = ∠C? Why or why not?
(iv) Is BD = CD? Why or why not?
Solution:
(i) The three pairs of equal parts in ∆ADB and ∆ADC are:
AD = AD (Common)
Hypotenuse AB = Hypotenuse AC (Given)
∠ADB = ∠ADC (Each = 90°)
(ii) ∵ A ↔ A, B ↔ C, D ↔ D
∴ ∆ADB ≅ ∆ADC
(iii) Since, ∆ADB ≅ ∆ADC
∴ Corresponding parts are equal.
∴ ∠B = ∠C
(iv) Also, \(\overline{B D}\) = \(\overline{C D}\)