Gujarat Board GSEB Solutions Class 7 Maths Chapter 8 રાશિઓની તુલના InText Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 8 રાશિઓની તુલના InText Questions
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 157)
એક કીડી પોતાના વજન કરતાં 50 ગણું વજન ઊંચકી શકે છે. જો આ તથ્ય માણસ પર લાગુ પાડવામાં આવે, તો તમે કેટલું વજન ઊંચકી શકો?
ઉત્તરઃ
હું મારા વજન કરતાં 50 ગણું વજન ઊંચકી શકું.
મારું વજન 35 કિગ્રા છે તેથી હું 35 × 50 = 1750 કિગ્રા વજન ઊંચકી શકું.
પાઠ્યપુસ્તકમાંથી (પાઠ્યપુસ્તક પાન નંબર 158)
કોષ્ટક પૂર્ણ કરો:
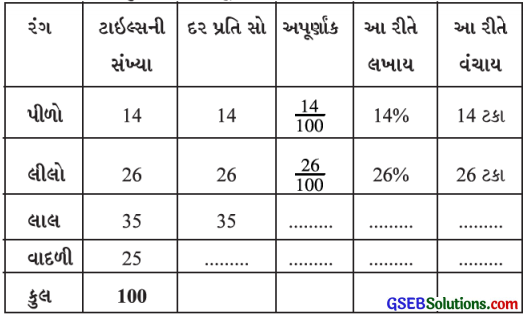
ઉત્તરઃ
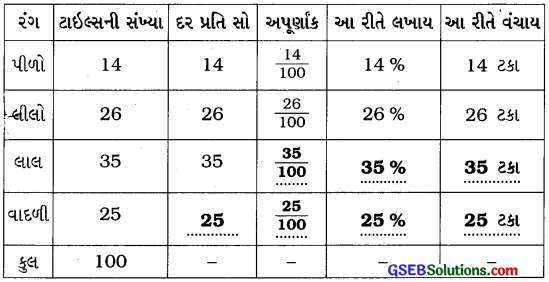
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 158)
1. નીચે આપેલી માહિતી માટે જુદી જુદી ઊંચાઈ ધરાવતાં બાળકોની સંખ્યાના ટકા શોધોઃ
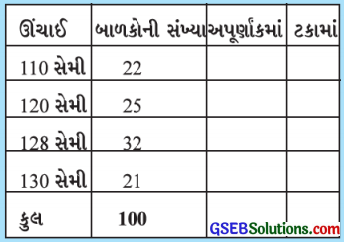
ઉત્તરઃ
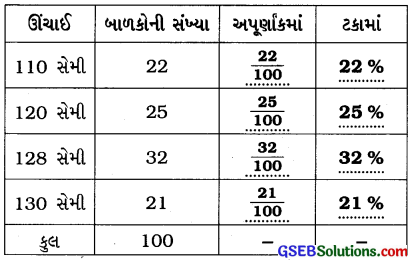
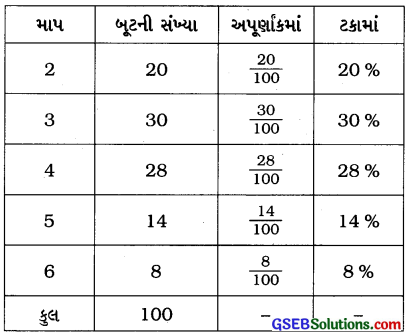
2. એક દુકાનમાં જુદાં જુદાં માપનાં બૂટની જોડની સંખ્યા નીચે પ્રમાણે છેઃ
માપ 2 : 20
માપ 3 : 30
માપ 4 : 28
માપ 5 : 14
માપ 6 : 8
આ માહિતીને કોષ્ટક સ્વરૂપે લખો અને દુકાનમાં ઉપલબ્ધ દરેક માપનાં બૂટની સંખ્યાના ટકા શોધો.
ઉત્તરઃ
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 159-160)
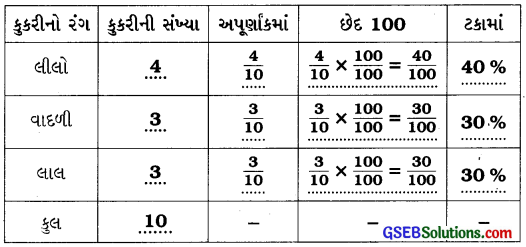
1. જુદા જુદા રંગની 10 કુકરીનો સંગ્રહ આપેલો છે:
કુલ કોષ્ટક પૂર્ણ કરો અને દરેક રંગની કુકરીની સંખ્યાના ટકા શોધો.
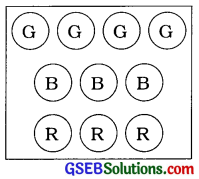
ઉત્તરઃ
2. માલા પાસે બંગડીઓનો સંગ્રહ છે. તેણી પાસે 20 સોનાની બંગડીઓ અને 10 ચાંદીની બંગડીઓ છે, તો આ દરેક પ્રકારની બંગડીઓની સંખ્યાના ટકા શોધો. પાઠ્યપુસ્તક પાન 159 પરના ઉદાહરણ પ્રમાણે શું તમે આ માહિતી કોષ્ટકમાં દર્શાવી શકો?
ઉત્તરઃ
માલા પાસે કુલ બંગડીઓ = 20 સોનાની + 10 ચાંદીની = 30
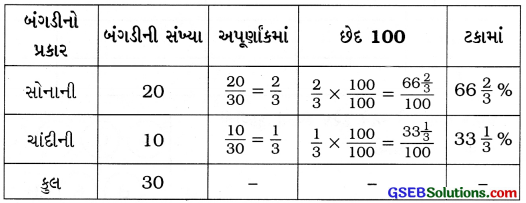
![]()
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 160)
1. નીચેનાં ઉદાહરણો જુઓ અને દરેકમાં તુલના કરવા માટે કઈ પદ્ધતિ યોગ્ય ગણાય તેની ચર્ચા કરો:
વાતાવરણની 1 ગ્રામ હવામાં:

ઉત્તરઃ
અહીં, વિભાગ (ii)માં આપેલી વિગત ટકાવારીમાં છે.
સરખામણી કરવા માટે વિભાગ (ii)ની વિગત વધુ સારી ગણાય.
2. એક શર્ટમાં :

ઉત્તરઃ
શર્ટના કાપડનું વણાટ સમજવા માટે (ii)માં આપેલી વિગત વધુ સારી ગણાય.
વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબર 161)
(i) (a) શું તમે કેકનો 50 % ભાગ ખાઈ શકો?
(b) શું તમે 100 % કેક ખાઈ શકો?
(c) શું તમે કેકનો 150 % ભાગ ખાઈ શકો?
(ii) (a) શું વસ્તુની કિંમત 50 %થી ઉપર જઈ શકે?
(b) શું વસ્તુની કિંમત 100 %થી ઉપર જઈ શકે?
(c) શું વસ્તુની કિંમત 150 %થી ઉપર જઈ શકે?
ઉત્તરઃ
(i) (a) હા, અમે કેકનો 50 % ભાગ ખાઈ શકીએ.
કારણઃ આખી કેક(100 %)માંથી 50 % (અડધી કેક) ખાઈ શકાય. આ બાબત શક્ય છે.
(b) હા, અમે 100 % કેક ખાઈ શકીએ.
કારણ: આખી કેક (100 %) ખાઈ શકાય. આ શક્ય છે.
(c) ના, અમે કેકનો 150 % ભાગ ન ખાઈ શકીએ.
કારણ કેકનો 100 % ભાગ શક્ય છે. તેથી વધુ ભાગ 150 % શક્ય નથી.
(ii) (a) હા, વસ્તુની કિંમત 50 %થી ઉપર જઈ શકે છે.
દા. ત., વસ્તુની કિંમત ₹ 10 હોય, તો નવી કિંમત ₹ 15થી ઉપર જઈ શકે છે.
(b) હા, વસ્તુની કિંમત 100 %થી ઉપર જઈ શકે છે.
દા. ત., વસ્તુની કિંમત ₹ 40 હોય, તો નવી કિંમત ₹ 80થી ઉપર જઈ શકે છે.
(c) હા, વસ્તુની કિંમત 150 %થી ઉપર જઈ શકે છે.
દા. ત., વસ્તુની કિંમત ₹ 80 હોય, તો નવી કિંમત ₹ 200થી ઉપર જઈ શકે છે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 161)
1. નીચેનાને ટકામાં ફેરવો?
(a) \(\frac {12}{16}\)
ઉત્તરઃ
\(\frac {12}{16}\) = \(\frac {12}{16}\) × 100%
= \(\frac {3}{4}\) × 100%
= 75%
(b) 3.5
ઉત્તરઃ
3.5 = \(\frac {35}{10}\) × 100%
= 35 × 10 %
= 350 %
(c) \(\frac {49}{50}\)
ઉત્તરઃ
\(\frac {49}{50}\) = \(\frac {49}{50}\) × 100%
= 49 × 2%
= 98 %
(d) \(\frac {2}{2}\)
ઉત્તરઃ
\(\frac {2}{2}\) = \(\frac {2}{2}\) × 100%
= 1 × 100%
= 100 %
(e) 0.05
ઉત્તરઃ
0.05 = 0.05 × 100 %
= \(\frac {5}{100}\) × 100 %
= 5 %
2. (i) 32 વિદ્યાર્થીઓમાંથી 8 વિદ્યાર્થીઓ ગેરહાજર છે, તો કેટલા ટકા વિદ્યાર્થીઓ ગેરહાજર ગણાય?
(ii) 25 રેડિયો છે, તેમાંના 16 રેડિયો ખરાબ છે, તો કેટલા ટકા રેડિયો ખરાબ છે?
(iii) એક દુકાનમાં 500 વસ્તુ છે. તેમાંથી 5 બગડેલી વસ્તુ છે, તો કેટલા ટકા વસ્તુ બગડેલી કહેવાય?
(iv) 120 મતદારો છે. તેમાંથી 90 મતદારોનો મત ‘હા’ છે, તો ‘હા’ મતોની સંખ્યાના ટકા શોધો.
ઉત્તરઃ
(i) વિદ્યાર્થીઓની કુલ સંખ્યા = 32
ગેરહાજર વિદ્યાર્થીઓની સંખ્યા = 8
∴ ગેરહાજર વિદ્યાર્થીઓની ટકાવારી

આમ, 25 % વિદ્યાર્થીઓ ગેરહાજર છે.
(ii) રેડિયોની કુલ સંખ્યા = 25
ખરાબ રેડિયોની સંખ્યા = 16

આમ, 64 % રેડિયો ખરાબ છે.
(iii) વસ્તુની કુલ સંખ્યા = 500
બગડેલી વસ્તુની સંખ્યા = 5

આમ, બગડેલી વસ્તુના ટકા 1 % છે.
(iv) કુલ મતદારોની સંખ્યા = 120
‘હા’ મત આપનાર મતદારોની સંખ્યા = 90
∴ ‘હા’ મત આપનાર મતદારોની ટકાવારી

આમ, ‘હા’ મતોની સંખ્યાના ટકા 75 % છે.
![]()
પાઠ્યપુસ્તકમાંથી (પાઠ્યપુસ્તક પાન નંબર 162)
કોષ્ટક જુઓ, અવલોકન કરો અને પૂર્ણ કરો:
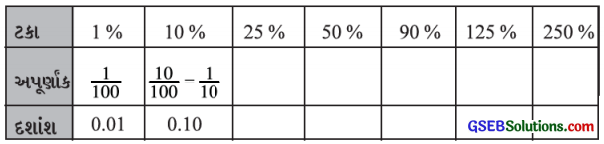
ઉત્તરઃ

પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 162)
1. ખાલી જગ્યા પૂરોઃ
(i) 35 % + ……… % = 100 %
(ii) 64 % + 20 % + …………… % = 100 %
(iii) 45 % = 100 % – …………… %
(iv) 70 % = …………… % – 30%
ઉત્તરઃ
(i) જુઓઃ 100 % – 35 % = 65 %
∴ 35 % + 65 % = 100 %
(ii) જુઓ: 64 % + 20 % = 84 %
અને 100 % – 84 % = 16 %
∴ 64 % + 20 % + 16 % = 100 %
(iii) જુઓઃ 100 % – 45 % = 55 %
∴ 45 % = 100 % – 55 %
(iv) જુઓઃ 70 % + 30 % = 100 %
∴ 70 % = 100% – 30 %
2. જો વર્ગના 65 % વિદ્યાર્થીઓ પાસે સાઈકલ હોય, તો વર્ગના કેટલા ટકા વિદ્યાર્થી ઓ પાસે સાઈકલ નથી?
ઉત્તરઃ
સાઇકલ હોય તેવા વિદ્યાર્થીઓ = 65 %
∴ સાઇકલ ન હોય તેવા વિદ્યાર્થીઓ = 100 % – 65 %
= (100 – 65) % = 35 %
કુલ વિદ્યાર્થીઓમાંથી 35 % ભાગના વિદ્યાર્થીઓ પાસે સાઇકલ નથી.
3. આપણી પાસે સફરજન, નારંગી અને કેરીથી ભરેલી ટોપલી છે. જો 50 % સફરજન, 30 % નારંગી હોય, તો કેટલા ટકા કેરી હશે?
ઉત્તરઃ
સફરજનનો ભાગ = 50 % નારંગીનો ભાગ = 30 %
∴ કુલ ફળોમાં સફરજન અને નારંગીનો ભાગ = 50 % + 30 %
= (50 + 30) % = 80 %
હવે, કુલ ફળો = 100 % જેમાં બાકીનાં ફળ કેરી છે.
∴ કેરીનો ભાગ = 100 % – 80 % = (100 – 80) % = 20 %
ટોપલીમાં 20 % કેરી હશે.
![]()
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબર 162)
ડ્રેસ તૈયાર કરવામાં આવેલા ખર્ચને ધ્યાનમાં લો.
20 % ભરતકામ પર, 50 % કાપડ પર, 30 % સિલાઈ પર
શું તમે આવાં વધુ ઉદાહરણો વિચારી શકો?
ઉત્તરઃ
માગ્યા મુજબનાં ઉદાહરણ નીચે પ્રમાણે છે :
(i) મારી પાસેની કુલ રકમમાંથી મેં 40 % રકમનાં પુસ્તકો, 25 % રકમની નોટબુકો અને 35 % રકમનો સ્કૂલ ડ્રેસ ખરીદ્યો.
(ii) અમે દિવાળીમાં પપ્પાના પગારના 28 % રકમના ફટાકડા, 42 % રકમની મીઠાઈ અને 30 % રકમનાં કપડાં ખરીદ્યાં.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 163)
નીચે દર્શાવેલ આકૃતિઓમાં કેટલા ટકા ભાગ છાયાંકિત છે?

ઉત્તરઃ
(i) આપેલી આકૃતિમાં કુલ 4 સરખા ભાગ કરેલા છે.
∴ દરેક ભાગ એ આખી આકૃતિનો \(\frac {1}{4}\) ભાગ છે.
આકૃતિમાં 4 ભાગમાંથી 3 ભાગ છાયાંકિત છે.
એટલે કે \(\frac {3}{4}\) ભાગ છાયાંકિત છે.
∴ છાયાંકિત ભાગની ટકાવારી = (\(\frac {3}{4}\) × 100) % = 75 %
(ii) આકૃતિમાં છાયાંતિ ભાગ , છે અને તે છે.
∴ છાયાંકિત કુલ ભાગ = \(\frac{1}{4}+\frac{1}{8}+\frac{1}{8}\)
= \(\frac{2+1+1}{8}\)
= \(\frac {4}{8}\)
= \(\frac {1}{2}\)
એટલે કે 3 ભાગ છાયાંતિ છે.
∴ છાયાંકિત ભાગની ટકાવારી = (\(\frac {1}{2}\) × 100) % = 50 %
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 164)
1. ઉકેલ મેળવોઃ
(a) 164ના 50 %
(b) 12ના 75 %
(c) 64ના 12%
ઉત્તરઃ
(a) 164ના 50 %
50 % = \(\frac {50}{100}\)
∴ 164ના 50% = 164 × \(\frac {50}{100}\) = 82
(b) 12ના 75 %
75 % = \(\frac {75}{100}\)
∴ 12ના 75 % = 12 × \(\frac {75}{100}\) = 9
(c) 64ના 12\(\frac {1}{2}\) %
12\(\frac {1}{2}\) % = \(\frac {25}{2}\) × \(\frac {1}{100}\)
∴ 64ના 12\(\frac {1}{2}\) % = 64 \(\frac {25}{2}\) × \(\frac {1}{100}\) = 8
2. એક વર્ગનાં 25 બાળકોમાંથી 8% બાળકોને વરસાદમાં ભીંજાવું ગમે છે, તો કેટલાં બાળકોને વરસાદમાં ભીંજાવું ગમે છે?
ઉત્તરઃ
25ના 8 % = 25 × \(\frac {8}{100}\) = 2
2 બાળકોને વરસાદમાં ભીંજાવું ગમે છે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 164)
1. કઈ સંખ્યાના 25 % એટલે 9?
ઉત્તરઃ
ધારો કે તે સંખ્યા x છે.
ના 25 % = x × \(\frac {25}{100}\)
હવે, xના 25 % એટલે 9
∴ x × \(\frac {25}{100}\) = 9
∴ x = \(\frac{100 \times 9}{25}\)
∴ x = 36
આમ, 36ના 25 % એટલે 9.
2. કઈ સંખ્યાના 75% એટલે 15?
ઉત્તરઃ
ધારો કે તે સંખ્યા ૪ છે.
ના 75 % = x × \(\frac {75}{100}\)
હવે, ના 75 % એટલે 15.
∴ x × \(\frac {75}{100}\) = 15
∴ x = \(\frac{15 \times 100}{75}\)
∴ x = 20
આમ, 20ના 75 % એટલે 15.
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 166)
1. 15 મીઠાઈઓને એવી રીતે વહેંચવામાં આવે કે મનુ અને સોનુને અનુક્રમે 20 % અને 80 % મીઠાઈ મળે.
ઉત્તરઃ
મનુનો ભાગ = 15 મીઠાઈનો 20 % ભાગ
= 15 × \(\frac {20}{100}\) મીઠાઈ = 3 મીઠાઈ
સોનુનો ભાગ = 15 મીઠાઈનો 80 % ભાગ
= 15 × \(\frac {80}{100}\) મીઠાઈ = 12 મીઠાઈ
2. ત્રિકોણના ખૂણાનો ગુણોત્તર 2 : 3 : 4 હોય, તો દરેક ખૂણાનું માપ શોધો.
ઉત્તરઃ
અહીં, ત્રિકોણના ત્રણે ખૂણાઓનું માપ 2 : 3 : 4ના પ્રમાણમાં છે.
આ પ્રમાણનો સરવાળો = 2 + 3 + 4 = 9
હવે, ત્રિકોણના ત્રણે ખૂણાઓનાં માપનો સરવાળો 180° થાય.
∴ પહેલા ખૂણાનું માપ = 180° × \(\frac {2}{9}\) = 40°
બીજા ખૂણાનું માપ = 180° × \(\frac {3}{9}\) = 60°
ત્રીજા ખૂણાનું માપ = 180° × \(\frac {4}{9}\) = 80°
આમ, ત્રિકોણના ત્રણ ખૂણાઓનાં માપ 40°, 60° અને 80° છે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 167)
1. વધારા અથવા ઘટાડાની ટકાવારી શોધો:
(i) શર્ટની કિંમત ₹ 280થી ઘટીને ₹ 210 થઈ છે.
(ii) કોઈ એક પરીક્ષામાં મળેલ ગુણ 20થી વધીને 30 થાય છે.
ઉત્તરઃ
(i) શર્ટની સામાન્ય કિંમત = ₹ 280
શર્ટની ઘટાડેલી કિંમત = ₹ 210
∴ શર્ટની કિંમતમાં થયેલો ઘટાડો = ₹ 280 – ₹ 210 = ₹ 70
∴ શર્ટની કિંમતમાં થયેલા ઘટાડાની ટકાવારી = \(\frac {70}{280}\) × 100 = 25 %
(ii) સામાન્ય ગુણ = ₹ 20
વધારતાં થયેલા ગુણ = ₹ 30
∴ ગુણમાં વધારો = 30 – 20 = 10
∴ ગુણમાં થયેલા વધારાની ટકાવારી = \(\frac {10}{20}\) × 100 = 50 %
2. મારી મમ્મી કહે છે કે તેમના બાળપણમાં પેટ્રોલ ₹ 10 પ્રતિ લિટર હતું. આજે એનો ભાવ ₹ 70 પ્રતિ લિટર છે. તો કિંમતમાં કેટલા ટકા વધારો થયો?
ઉત્તરઃ
પહેલાં પેટ્રોલની પ્રતિલિટર કિંમત = ₹ 10
હવે, પેટ્રોલની પ્રતિલિટર કિંમત = ₹ 70
∴ પેટ્રોલની કિંમતમાં પ્રતિલિટર વધારો = ₹ 70 – ₹ 10 = ₹ 60
∴ પેટ્રોલની કિંમતમાં પ્રતિલિટર વધારાની ટકાવારી = \(\frac {60}{10}\) × 100
= 600
પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબર 169)
1. એક દુકાનદાર એક ખુરશી ₹ 375માં ખરીદે છે અને ₹ 400માં તેને વેચે છે. હવે, દુકાનદારે મેળવેલ નફાની ટકાવારી શોધો.
ઉત્તરઃ
ખુરશીની મૂ. કિં. = ₹ 375 અને ખુરશીની વે.કિં. = ₹ 400
અહીં, વે.કિ. > મૂ. કિ.
∴ વેપારીને નફો થાય છે.
નફો = વે.કિ. – મૂ. કિ.
∴ નફો = ₹ 400 – ₹ 375 = ₹ 25
વેપારીના નફાની ટકાવારી = \(\frac {25}{375}\) × 100 = \(\frac {20}{3}\) % = 6\(\frac {2}{3}\) %
વેપારીને 6\(\frac {2}{3}\)% નફો થાય છે.
2. ₹ 50માં એક વસ્તુ ખરીદાય છે અને તેને 12 %ના નફા સાથે વેચવામાં આવે છે, તો વેકિં. શોધો.
ઉત્તરઃ
વસ્તુની મૂ. કિં. = ₹ 50
વસ્તુ પર લેવાતા નફાના ટકા = 12 %
∴ વસ્તુના વેચાણમાં મળતો નફો = ₹ (50 × \(\frac {12}{100}\)) = ₹ 6
હવે, વસ્તુની વે,કિં. = મૂ. કિ. + નફો
= ₹ 50 + ₹ 6 = ₹ 56
આમ, વસ્તુની વે.કિ. ₹ 56 હોય.
3. ₹ 250માં વેચવામાં આવતી વસ્તુ પર 5 % નફો મેળવાય છે, તો તેની ૫. કિં. કેટલી હશે?
ઉત્તરઃ
ધારો કે વસ્તુની ૫. કિં. = ₹ x
વસ્તુ પર લેવાતા નફાના ટકા = 5%
વસ્તુ પર થતો નફો = ₹ x × \(\frac {5}{100}\)
= ₹ \(\frac{x}{20}\)
હવે, વે.કિ. = ૫. કિ. + નફો
250 = x + \(\frac{x}{20}\)
250 = \(\frac{20 x+x}{20}\)
∴ 250 × 20 = 21x
∴ 5000 = 21x
∴ x = \(\frac {5000}{21}\)
∴ x = 238\(\frac {2}{21}\)
વસ્તુની ૫. કિં. ₹ 238\(\frac {2}{21}\) હોય.
બીજી રીત:
5% નફો એટલે ₹ 100ની ૫. કિં.
પર નફો = ₹ 5
∴ વે.કિ. = . કિં. + નફો
= ₹ 100 + ₹ 5 = ₹ 105
= ₹ 105 વેકિ. હોય, તો પ. કિ.
= ₹ 100
∴ ₹ 250 વેકિ. હોય, તો પ. કિ.
= \(\frac {250}{105}\) × 100 = \(\frac {250}{21}\) × 20
= \(\frac {5000}{21}\) = 238\(\frac {2}{21}\)
વસ્તુની ૫. કિ. ₹ 238\(\frac {2}{21}\) હોય.
4. એક વસ્તુ 5% ખોટ સાથે ₹ 540માં વેચવામાં આવે છે. તેની પ. કિં. શું હશે?
ઉત્તરઃ
ધારો કે વસ્તુની ૫. કિં. = ₹ x
વસ્તુના વેચાણમાં થતી ખોટના ટકા = 5 %
વસ્તુના વેચાણમાં થતી ખોટ = ₹ x × \(\frac {5}{100}\) = ₹ \(\frac{x}{20}\)
હવે, વેકિં. = ૫. કિ. – ખોટ
∴ 540 = x – \(\frac{x}{20}\)
540 = \(\frac{20 x-x}{20}\)
∴ 540 × 20 = 19x
∴ 10,800 = 19x
∴ x = \(\frac{10,800}{19}\)
∴ x = 568\(\frac {8}{19}\)
વસ્તુની ૫. કિં. ₹ 568\(\frac {8}{19}\) હોય.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 170)
1. 5 ટકા વાર્ષિક વ્યાજના દરે ₹ 10,000 જમા કરાવવામાં આવે છે, તો એક વર્ષના અંતે મળતું વ્યાજ શોધો.
ઉત્તરઃ
અહીં, મુદ્દલ P = ₹ 10,000; વ્યાજનો દર R = 5 % અને મુદત T = 1 વર્ષ
∴ સાદું વ્યાજ I = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{10,000 \times 5 \times 1}{100}\) = ₹ 500
વર્ષના અંતે વ્યાજ ₹ 500 થાય.
2. 7 ટકા વાર્ષિક વ્યાજના દરે ₹ 3500 આપવામાં આવે છે, તો 2 વર્ષના અંતે મળતું વ્યાજ શોધો.
ઉત્તરઃ
અહીં, મુદ્દલ P = ઉત્તરઃ 3500, વ્યાજનો દર R = 7 % અને મુદત T = 2 વર્ષ
∴ સાદું વ્યાજ I = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{3500 \times 7 \times 2}{100}\) = ₹ 490
મુદતના અંતે વ્યાજ ₹ 490 મળે.
3. 6.5 ટકા વાર્ષિક વ્યાજના દરે ₹ 6050 લેવામાં આવે છે, તો 3 વર્ષના અંતે ચૂકવવું પડતું વ્યાજ અને વ્યાજમુદ્દલ શોધો.
ઉત્તરઃ
અહીં, મુદ્દલ P = ₹ 6050, વ્યાજનો દર R = 6.5 % અને મુદત T = 3 વર્ષ
∴ સાદું વ્યાજ I = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{6050 \times 6.5 \times 3}{100}\)
= \(\frac{6050 \times 65 \times 3}{10 \times 100}\)
= ₹ \(\frac{117975}{100}\)
= ₹ 1179.75
∴ વ્યાજ = ₹ 1179.75
વ્યાજમુદ્દલ = મુદ્દલ + વ્યાજ
= ₹ 6050 + ₹ 1179.75 = ₹ 7229.75
મુદતને અંતે વ્યાજસહિત ₹ 7229.75 આપવા પડે.
4. જો 2 વર્ષ માટે 3.5 ટકા વાર્ષિક વ્યાજના દરે ₹ 7000 લેવામાં આવે, તો 2 વર્ષના અંતે ચૂકવવું પડતું વ્યાજમુદ્દલ શોધો.
ઉત્તરઃ
અહીં, મુદ્દલ P = ₹ 7000, વ્યાજનો દર R = 3.5 % અને મુદત T = 2 વર્ષ
∴ સાદું વ્યાજ I = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{7000 \times 3.5 \times 2}{100}\)
= \(\frac{7000 \times 35 \times 2}{10 \times 100}\)
= ₹ 490
વ્યાજ = ₹ 490
વ્યાજમુદ્દલ = મુદ્દલ + વ્યાજ
= ₹ 7000 + ₹ 490 = ₹ 7490
મુદતને અંતે વ્યાજસહિત ₹ 7490 ચૂકવવા પડે.
![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબર 171)
1. તમારા બેંક ખાતામાં ₹ 2400 જમા છે અને વ્યાજનો વાર્ષિક દર 5 ટકા – છે. કેટલાં વર્ષો બાદ વ્યાજ ₹ 240 થશે?
ઉત્તરઃ
અહીં, મુદ્દલ P = ₹ 2400, વ્યાજનો દર R = 5 %, મુદત T = ?, વ્યાજ I = ₹ 240
∴ સાદું વ્યાજ I = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
∴ 240 = \(\frac{2400 \times 5 \times \mathrm{T}}{100}\)
∴ 240 = 24 × 5 × T
∴ T = \(\frac{240}{24 \times 5}\)
∴ T = 2
મુદત 2 વર્ષ
આમ, 2 વર્ષને અંતે વ્યાજ ₹ 240 થશે.
2. કોઈ રકમનું વાર્ષિક 5 ટકા લેખે 3 વર્ષનું વ્યાજ ₹ 450 થાય છે, તો તે રકમ શોધો.
ઉત્તરઃ
અહીં, મુદ્દલ P = ?, વ્યાજનો દર R = 5 %, મુદત T = 3 વર્ષ, વ્યાજ I = ₹ 450
∴ સાદું વ્યાજ I = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
∴ 450 = \(\frac{\mathrm{P} \times 5 \times 3}{100}\)
∴ P = \(\frac{450 \times 100}{5 \times 3}\)
∴ P = ₹ 3000
મુદ્દલ ₹ 3000
આમ, માગેલું મુદ્દલ ₹ 3000 છે.