Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 9 Rational Numbers Ex 9.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 9 Rational Numbers Ex 9.2
![]()
Question 1.
Find the sum:
(i) \(\frac { 5 }{ 4 }\) + ( \(\frac { -11 }{ 4 }\) )
(ii) \(\frac { 5 }{ 3 }\) + \(\frac { 3 }{ 5 }\)
(iii) \(\frac { -9 }{ 10 }\) + \(\frac { 22 }{ 15 }\)
(iv) \(\frac { -3 }{ -11 }\) and \(\frac { 5 }{ 9 }\)
(v) \(\frac { -8 }{ 19 }\) + \(\frac { (-2) }{ 57 }\)
(vi) \(\frac { -2 }{ 3 }\) + 0
(vii) – 2\(\frac { 1 }{ 3 }\) + 4\(\frac { 3 }{ 5 }\)
Solution:
(i) \(\frac { 5 }{ 4 }\) + ( \(\frac { -11 }{ 4 }\) )
We have \(\frac { 5 }{ 4 }\) + ( \(\frac { -11 }{ 4 }\) ) = \(\frac { 5+(-11) }{ 4 }\) = \(\frac { -6 }{ 4 }\)
= \(\frac { -3 }{ 2 }\) or -1\(\frac { 1 }{ 2 }\)
(ii) \(\frac { 5 }{ 3 }\) + \(\frac { 3 }{ 5 }\)
∵ LCM of 3 and 5 is 15.

(iv) \(\frac { -3 }{ -11 }\) and \(\frac { 5 }{ 9 }\)
∵ LCM of 11 and 9 is 99.
∴ \(\frac { -3 }{ -11 }\) = \(\frac { (-3)×9 }{ (-11)×9 }\) = \(\frac { -27 }{ -99 }\) = \(\frac { 27 }{ 99 }\)
and \(\frac { 5 }{ 9 }\) = \(\frac { 5×11 }{ 9×11 }\) = \(\frac { 55 }{ 99 }\)

(vi) \(\frac { -2 }{ 3 }\) + 0
We have \(\frac { -2 }{ 3 }\) + 0 = \(\frac { -2 }{ 3 }\) + \(\frac { 0 }{ 3 }\) = \(\frac { -2+0 }{ 3 }\) = \(\frac { -2 }{ 3 }\)
Thus, \(\frac { -2 }{ 3 }\) + 0 = \(\frac { -2 }{ 3 }\)
(vii) – 2\(\frac { 1 }{ 3 }\) + 4\(\frac { 3 }{ 5 }\)

![]()
Question 2.
Find:
(i) \(\frac { 7 }{ 24 }\) – \(\frac { 17 }{ 36 }\)
(ii) \(\frac { 5 }{ 63 }\) – ( \(\frac { -6 }{ 21 }\) )
(iii) \(\frac { -6 }{ 13 }\) – \(\frac { -7 }{ 15 }\)
(iv) \(\frac { -3 }{ 8 }\) – \(\frac { 7 }{ 11 }\)
(v) -2\(\frac { 1 }{ 9 }\) – 6
Solution:
(i) \(\frac { 7 }{ 24 }\) – \(\frac { 17 }{ 36 }\)
∵ LCM of 24 and 36 is 72.

(ii) \(\frac { 5 }{ 63 }\) – ( \(\frac { -6 }{ 21 }\) )
∵ LCM of 63 and 21 is 63.

Thus, \(\frac { 5 }{ 63 }\) – ( \(\frac { -6 }{ 21 }\) = \(\frac { -13 }{ 72 }\)
(iii) \(\frac { -6 }{ 13 }\) – \(\frac { -7 }{ 15 }\)
∵ LCM of 13 and 15 is 195.

(v) -2\(\frac { 1 }{ 9 }\) – 6

![]()
Question 3.
Find the product:
(i) \(\frac { 9 }{ 2 }\) x ( \(\frac { -7 }{ 4 }\) )
(ii) \(\frac { 3 }{ 10 }\) x (-9)
(iii) \(\frac { -6 }{ 5 }\) x \(\frac { 9 }{ 11 }\)
(iv) \(\frac { 3 }{ 7 }\) x \(\frac { -2 }{ 5 }\)
(v) \(\frac { 3 }{ 11 }\) x \(\frac { 2 }{ 5 }\)
(vi) \(\frac { 3 }{ -5 }\) x \(\frac { -5 }{ 3 }\)
Solution:
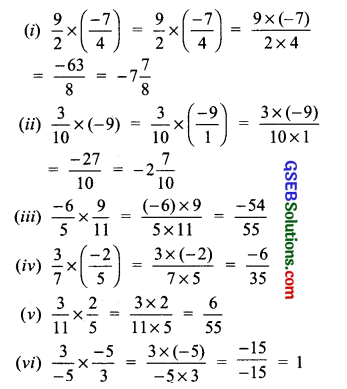
Question 4.
Draw the number line and represent the following rational numbers on it:
(i) (- 4) ÷ \(\frac { 2 }{ 3 }\)
(ii) \(\frac { -3 }{ 5 }\) ÷ 2
(iii) \(\frac { -4 }{ 5 }\) ÷ (-3)
(iv) \(\frac { -1 }{ 8 }\) ÷ \(\frac { 3 }{ 4 }\)
(v) \(\frac { -2 }{ 13 }\) ÷ \(\frac { 1 }{ 7 }\)
(vi) \(\frac { -7 }{ 12 }\) ÷ ( \(\frac { -2 }{ 13 }\) )
(vii) \(\frac { 3 }{ 13 }\) ÷ ( \(\frac { -4 }{ 65 }\) )
Solution:
(i) (- 4) ÷ \(\frac { 2 }{ 3 }\)

Thus, (- 4) ÷ \(\frac { 2 }{ 3 }\) = – 6
(ii) \(\frac { -3 }{ 5 }\) ÷ 2
∵ The reciprocal of 2 is \(\frac { 1 }{ 2 }\)
∴ \(\frac { -3 }{ 5 }\) ÷ 2 = \(\frac { -3 }{ 5 }\) x \(\frac { 1 }{ 2 }\)
= \(\frac { (-3)×1 }{ 5×2 }\) = \(\frac { -3 }{ 10 }\)
Thus, \(\frac { -3 }{ 5 }\) ÷ 2 = \(\frac { -3 }{ 10 }\)
![]()
(iii) \(\frac { -4 }{ 5 }\) ÷ (-3)

(iv) \(\frac { -1 }{ 8 }\) ÷ \(\frac { 3 }{ 4 }\)

(vi) \(\frac { -7 }{ 12 }\) ÷ ( \(\frac { -2 }{ 13 }\) )
∵ The reciprocal of \(\frac { -2 }{ 13 }\) is ( \(\frac { 13 }{ 2 }\)
∴ \(\frac { -7 }{ 12 }\) ÷ ( \(\frac { -2 }{ 13 }\) ) = \(\frac { -7 }{ 12 }\) x ( \(\frac { 13 }{ 2 }\)
= \(\frac { (-7)×(-13) }{ 12×2 }\)
= \(\frac { 91 }{ 24 }\) or 3\(\frac { 19 }{ 24 }\)
Thus,
\(\frac { -7 }{ 12 }\) ÷ ( \(\frac { -2 }{ 13 }\) )
= 3\(\frac { 19 }{ 24 }\)
= \(\frac { 91 }{ 24 }\) or 3\(\frac { 19 }{ 24 }\)
Thus,
\(\frac { -7 }{ 12 }\) ÷ ( \(\frac { -2 }{ 13 }\) )
= 3\(\frac { 19 }{ 24 }\)
![]()
(vii) \(\frac { 3 }{ 13 }\) ÷ ( \(\frac { -4 }{ 65 }\) )
