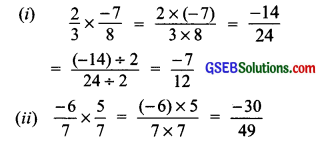Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 9 Rational Numbers InText Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 9 Rational Numbers InText Questions
![]()
Try These (Page 174)
Question 1.
Is the number \(\frac { 2 }{ -3 }\) rational? Think about it.
Solution:
Yes, \(\frac { 2 }{ -3 }\) is a rational number,
∵ 2 and – 3 are integers and – 3 ≠ 0.
Question 2.
List ten rational numbers.
Solution:
Following are ten rational numbers:
\(\frac { 1 }{ 3 }\), \(\frac { 2 }{ -3 }\), \(\frac { 4 }{ 5 }\), \(\frac { 1 }{ -6 }\), \(\frac { -3 }{ – 4 }\) 5.8, 2\(\frac { 4 }{ 5 }\), 0.93, 18 and 11.07.
Note.
1. ‘0’ can be written as \(\frac { 0 }{ 2 }\) or \(\frac { 0 }{ 15 }\), etc. Hence, it is a rational number.
2. A natural number can be written as 5 = \(\frac { 5 }{ 1 }\) or 108
= \(\frac { 108 }{ 1 }\)
Hence, it is also a rational number.
![]()
Try These (Page 175)
Question 1.
Fill in the boxes:
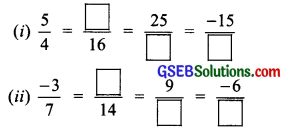
Solution:
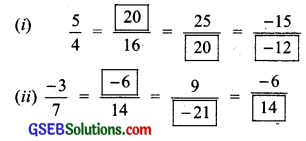
Try These (Page 175)
Question 1.
Is 5 a positive rational number?
Solution:
Yes, 5 or \(\frac { 5 }{ 1 }\) is having both its numerator and denominator as positive.
∴ It is a positive rational number.
Question 2.
List five more positive rational numbers.
Solution:
\(\frac { 1 }{ 7 }\), \(\frac { 3 }{ 8 }\), \(\frac { 5 }{ 17 }\), \(\frac { 2 }{ 9 }\) and \(\frac { 5 }{ 18 }\) are positive rational numbers.
![]()
Try These (Page 176)
Question 1.
Is – 8 a negative rational number?
Solution:
Yes, – 8 or \(\frac { -8 }{ 1 }\) is a negative rational number, because its numerator is a negative integer.
Question 2.
List five more negative rational numbers.
Solution:
Five negative rational numbers are as follows:
\(\frac { – 5 }{ 9 }\), \(\frac { -6 }{ 11 }\), \(\frac { -3 }{ 13 }\), \(\frac { 3 }{ -10 }\) and \(\frac { -1 }{ 7 }\)
Try These (Page 176)
Question 1.
Which of these are negative rational numbers?
(i) \(\frac { -2 }{ 3 }\)
(ii) \(\frac { 5 }{ 7 }\)
(iii) \(\frac { 3 }{ -5 }\)
(iv) 0
(v) \(\frac { 6 }{ 11 }\)
(vi) \(\frac { -2 }{ -9 }\)
Solution:
(i) \(\frac { -2 }{ 3 }\) is a negative rational number.
(ii) \(\frac { 5 }{ 7 }\) is a positive rational number.
(iii) \(\frac { 3 }{ -5 }\) is a negative rational number.
(iv) 0 is neither a positive nor a negative rational number.
(v) \(\frac { 6 }{ 11 }\) is a positive rational number.
(vi) \(\frac { -2 }{ -9 }\) is a positive rational number.
∴ (i) \(\frac { -2 }{ 3 }\) and (ii) \(\frac { 3 }{ -5 }\) are negative rational numbers.
Try These (Page 178)
Question 1.
Find the standard form of:
(i) \(\frac { -18 }{ 45 }\)
(ii) \(\frac { -12 }{ 18 }\)
Solution:
(i) Since HCF of 18 and 45 is 9.
∴ \(\frac { -18 }{ 45 }\) = \(\frac { (-18)÷9 }{ 45÷9 }\) = \(\frac { -2 }{ 5 }\)
Thus, the standard form of is \(\frac { -18 }{ 45 }\) is \(\frac { -2 }{ 5 }\)
(ii) Since, HCF of 12 and 18 is 6.
∴ \(\frac { -12 }{ 18 }\) = \(\frac { (-12)÷6 }{ 18÷6 }\) = \(\frac { -2 }{ 3 }\)
Thus, the standard form of \(\frac { -12 }{ 18 }\) is \(\frac { -2 }{ 3 }\)
![]()
Try These (Page 181)
Question 1.
Find five rational numbers between \(\frac { -5 }{ 7 }\) and \(\frac { -3 }{ 8 }\).
Solution:
First we convert the given rational numbers with common denominators.
∵ LCM of 7 and 8 is 56.
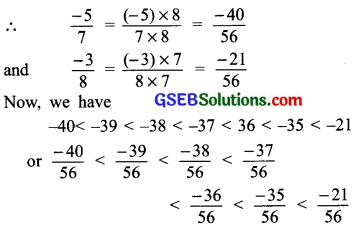
Thus, the five rational numbers, between \(\frac { -5 }{ 7 }\) and \(\frac { -3 }{ 8 }\) are:
\(\frac { -39 }{ 56 }\), \(\frac { -38 }{ 56 }\), \(\frac { -37 }{ 56 }\), \(\frac { -36 }{ 56 }\), \(\frac { -35 }{ 56 }\)
or \(\frac { -39 }{ 56 }\), \(\frac { -19 }{ 28 }\), \(\frac { -37 }{ 56 }\), \(\frac { -9 }{ 14 }\), \(\frac { -5 }{ 8 }\)
Try These (Page 185)
Question 1.
Find:
(i) \(\frac { -13 }{ 7 }\) + \(\frac { 6 }{ 7 }\)
(ii) \(\frac { 19 }{ 5 }\) + \(\frac { -7 }{ 5 }\)
Solution:

Question 2.
Find:
(i) \(\frac { -3 }{ 7 }\) + \(\frac { 2 }{ 3 }\)
(ii) \(\frac { -5 }{ 6 }\) + \(\frac { -3 }{ 11 }\)
Solution:
(i) \(\frac { -3 }{ 7 }\) + \(\frac { 2 }{ 3 }\)
∵ LCM of 7 and 3 is 21.
∴ \(\frac { -3 }{ 7 }\) = \(\frac { (-3)×3 }{ 7×3 }\) = \(\frac { -9 }{ 21 }\)
and \(\frac { 2 }{ 3 }\) = \(\frac { 2×7 }{ 3×7 }\) = \(\frac { 14 }{ 21 }\)
∴ \(\frac { -3 }{ 7 }\) + \(\frac { 2 }{ 3 }\) = \(\frac { -9 }{ 21 }\) + \(\frac { 14 }{ 21 }\)
= \(\frac { -9+14 }{ 21 }\)
= \(\frac { 5 }{ 21 }\)
(ii) \(\frac { -5 }{ 6 }\) + \(\frac { -3 }{ 11 }\)
Since, LCM of 6 and 11 is 66.
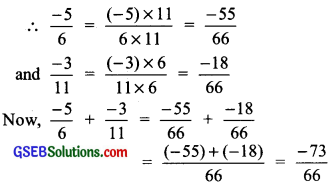
Try These (Page 186)
Question 1.
What will be the additive inverse of \(\frac { -3 }{ 9 }\)? \(\frac { -9 }{ 11 }\)?\(\frac { 5 }{ 7 }\)?
Solution:
Additive inverse of \(\frac { -3 }{ 9 }\) is \(\frac { 3 }{ 9 }\)
Additive inverse of \(\frac { -9 }{ 11 }\) is \(\frac { 9 }{ 11 }\)
Additive inverse of \(\frac { 5 }{ 7 }\) is \(\frac { -5 }{ 7 }\)
![]()
Try These (Page 187)
Question 1.
Find:
(i) \(\frac { 7 }{ 9 }\) – \(\frac { 2 }{ 5 }\)
(ii) 2\(\frac { 1 }{ 5 }\) – \(\frac { -1 }{ 3 }\)
Solution:

Try These (Page 188)
Question 1.
What will be
(i) \(\frac { -3 }{ 5 }\) x 7?
(ii) \(\frac { -6 }{ 5 }\) x (-2)?
Solution:
(i) \(\frac { -3 }{ 5 }\) x 7 = \(\frac { (-3)×7 }{ 5 }\) = \(\frac { -21 }{ 5 }\)
(ii) \(\frac { -6 }{ 5 }\) x (-2) = \(\frac { -6×(-2) }{ 5 }\) = \(\frac { 12 }{ 5 }\)
Note:
We multiply two rational numbers in the following way:
(i) Multiply the numerators of the rational numbers.
(ii) Multiply the denominators of the rational numbers.
(iii) Then product = ![]()
For example:
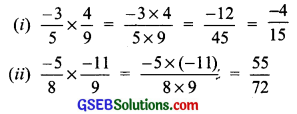
![]()
Try These (Page 188)
Question 1.
Find:
(i) \(\frac { -3 }{ 4 }\) x \(\frac { 1 }{ 7 }\)
(ii) \(\frac { 2 }{ 3 }\) x \(\frac { -5 }{ 9 }\)
Solution:

Try These (Page 189)
Question 1.
What will be the reciprocal of \(\frac { -6 }{ 11 }\) and \(\frac { -8 }{ 5 }\)?
Solution:
(i) Reciprocal of \(\frac { -6 }{ 11 }\) is \(\frac { 11 }{ -6 }\)
(ii) Reciprocal of \(\frac { -8 }{ 5 }\) is \(\frac { -5 }{ 8 }\).
To divide one rational number by the other rational number, we multiply the rational number by the reciprocal of the other. For example,

Try These (Page 190)
Question 1.
Find:
(i) \(\frac { 2 }{ 3 }\) x \(\frac { -7 }{ 8 }\)
(ii) \(\frac { -6 }{ 7 }\) x \(\frac { 5 }{ 7 }\)
Solution: