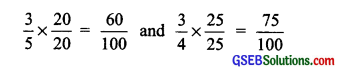Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 1 Rational Numbers Ex 1.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 1 Rational Numbers Ex 1.2
Question 1.
Represent these numbers on the number line.
- \(\frac { 7 }{ 4 }\)
- \(\frac { -5 }{ 6 }\)
Solution:
(i) To represent \(\frac { 7 }{ 4 }\) we make 7 markings each at a distance equal to \(\frac { 1 }{ 4 }\) on the right of 0.
The 7th point represents the rational number \(\frac { 7 }{ 4 }\) as shown in the figure.

The point A \(\frac { 7 }{ 4 }\).
(ii) To represent (\(\frac { 7 }{ 4 }\)) on the nmber Line, we make 5 each at a distance equal to \(\frac { 1 }{ 6 }\) on the left of 0. We consider the 5th point as shwn in the figure
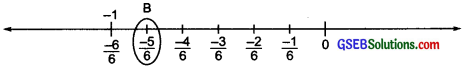
The point B represent (\(\frac { -5 }{ 6 }\))
![]()
Question 2.
Represent \(\frac { -2 }{ 11 }\), \(\frac { -5 }{ 11 }\), \(\frac { -9 }{ 11 }\). on the number line.
Solution:
TO represent \(\frac { -2 }{ 11 }\), \(\frac { -5 }{ 11 }\) and \(\frac { -9 }{ 11 }\) on a number line, we make 11 marking each being equal to distance \(\frac { 1 }{ 11 }\) on the left of 0.

- The point A represent \(\frac { -2 }{ 11 }\)
- The point B represent \(\frac { -5 }{ 11 }\)
- The point C represent \(\frac { -9 }{ 11 }\)
Question 3.
Write five rational numbers which are smaller than 2.
Solution:
There can be unlimited rational numbers smaller than 2. Five of them are:
0, -1, \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 2 }\), 1
![]()
Question 4.
Find ten rational numbers between \(\frac { -2 }{ 5 }\) and \(\frac { 1 }{ 2 }\)
Solution:
To convert \(\frac { -2 }{ 5 }\) and \(\frac { 1 }{ 2 }\) having the same denominators:
We have \(\frac { -2 }{ 5 }\) = \(\frac{-2 \times 4}{5 \times 4}\) = \(\frac { -8 }{ 20 }\) and \(\frac { 1 }{ 2 }\) = \(\frac{1 \times 10}{2 \times 10}\) = \(\frac { 10 }{ 20 }\)
∵ The rational numbers between \(\frac { 10 }{ 20 }\) and \(\frac { -8 }{ 20 }\) are \(\frac { 9 }{ 20 }\), \(\frac { 8 }{ 20 }\), \(\frac { 7 }{ 20 }\), \(\frac { 6 }{ 20 }\), …., \(\frac { -6 }{ 20 }\) , \(\frac { -7 }{ 20 }\)
We can take any 10 of them.
∵ ten rational nnumbers between \(\frac { -2 }{ 5 }\) and \(\frac { 1 }{ 2 }\) are:
(i) \(\frac { 9 }{ 20 }\)
(ii) \(\frac { 8 }{ 20 }\)
(iii) \(\frac { 7 }{ 20 }\)
(iv) \(\frac { 6 }{ 20 }\)
(v) \(\frac { 5 }{ 20 }\)
(vi) \(\frac { 4 }{ 20 }\)
(vii) \(\frac { 3 }{ 20 }\)
(viii) \(\frac { 2 }{ 20 }\)
(ix) \(\frac { 1 }{ 20 }\)
(x) 0
Question 5.
Find five rational numbers between:
- \(\frac { 2 }{ 3 }\) and \(\frac { 4 }{ 5 }\)
- \(\frac { -3 }{ 2 }\) and \(\frac { 5 }{ 3 }\)
- \(\frac { 1 }{ 4 }\) and \(\frac { 1 }{ 2 }\)
solution:
(i) Coverting \(\frac { 2 }{ 3 }\) and \(\frac { 4 }{ 5 }\) having same denominators such that difference between the numerators is more than 5.
We have \(\frac { 2 }{ 3 }\) = \(\frac{2 \times 20}{3 \times 20}\) = \(\frac { 40 }{ 60 }\) and \(\frac { 4 }{ 5 }\) = \(\frac{4 \times 12}{5 \times 12}\) = \(\frac { 48 }{ 60 }\)
Now, any five rational number between
\(\frac{40}{60}\left(=\frac{2}{3}\right)\) and \(\frac{48}{60}\left(=\frac{4}{5}\right)\) are: \(\frac { 41 }{ 60 }\), \(\frac { 42 }{ 60 }\), \(\frac { 43 }{ 60 }\) , \(\frac { 44 }{ 60 }\), \(\frac { 45 }{ 60 }\)
(ii) Converting \(\frac { -3 }{ 2 }\) and \(\frac { 5 }{ 3 }\) with same denominators, we have
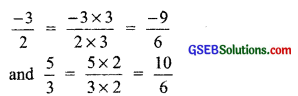
∴ Five rational numbers between
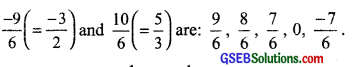
(iii) Converting \(\frac { 1 }{ 4 }\) and \(\frac { 1 }{ 2 }\) to rational numbers with the same denominators, we have
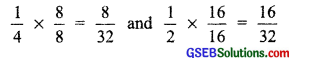
∴ Five rational numbers between \(\frac { 1 }{ 4 }\) and \(\frac { 1 }{ 2 }\) i.e., \(\frac { 8 }{ 32 }\) and \(\frac { 16 }{ 32 }\) are: \(\frac { 9 }{ 32 }\), \(\frac { 10 }{ 32 }\), \(\frac { 11 }{ 32 }\), \(\frac { 12 }{ 32 }\), \(\frac { 13 }{ 32 }\)
![]()
Question 6.
Write five rational numbers greater than – 2.
Solution:
Five rational numbers greater than – 2 are: \(\frac { -3 }{ 2 }\), -1, \(\frac { -1 }{ 2 }\), 0, \(\frac { 1 }{ 2 }\)
Note: There ten rationalnumbers greater than – 2
Question 7.
Find the rational numbers between \(\frac { 3 }{ 5 }\) and \(\frac { 3 }{ 4 }\).
Solution:
Converting \(\frac { 3 }{ 5 }\) and \(\frac { 3 }{ 4 }\) such that they between \(\frac { 3 }{ 4 }\) and \(\frac { 3 }{ 4 }\) such that they have common denominators and their numerators have difference of more than 10, i.each