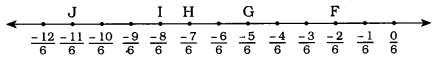Gujarat Board GSEB Solutions Class 8 Maths Chapter 1 સંમેય સંખ્યાઓ InText Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 1 સંમેય સંખ્યાઓ InText Questions
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 4)
નીચેના કોષ્ટકમાં ખાલી જગ્યા પૂરોઃ
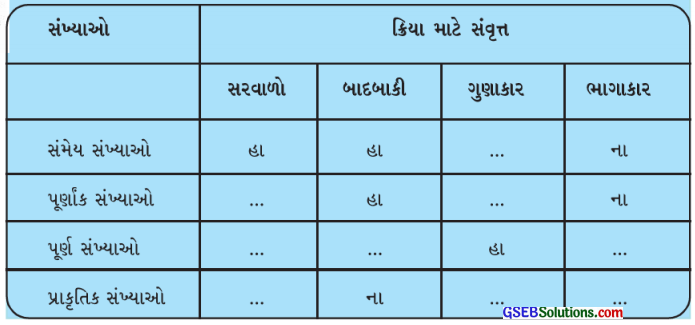
ઉત્તરઃ
આપણે સંમેય સંખ્યાઓના, પૂર્ણાંક સંખ્યાઓના, પૂર્ણ સંખ્યાઓના અને પ્રાકૃતિક સંખ્યાઓના સરવાળા, બાદબાકી, ગુણાકાર અને ભાગાકાર વિશે સંવૃત્તતાના ગુણધર્મોનો અભ્યાસ કર્યો. તે પરથી આગળના કોષ્ટકમાં નીચે પ્રમાણે જવાબ લખાશેઃ
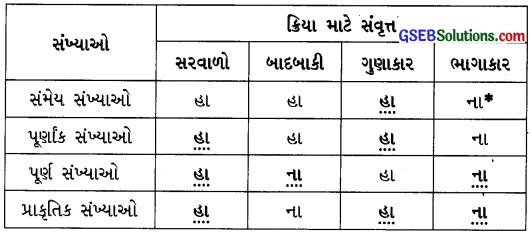
નોંધ: સંમેય સંખ્યા ભાગાકાર વિશે સંવૃત્ત નથી તે જુઓ.
દા. ત.\(\frac {2}{3}\) ÷ 0 = ? એ વ્યાખ્યાયિત નથી. માટે કોષ્ટકમાં જવાબ “ના” છે.
![]()
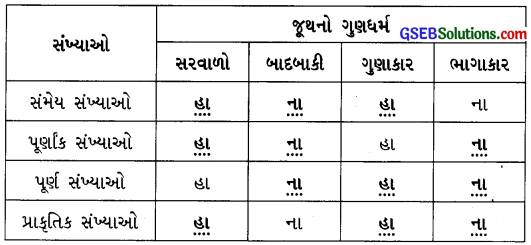
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 6)
નીચેનું કોષ્ટક પૂર્ણ પૂરોઃ
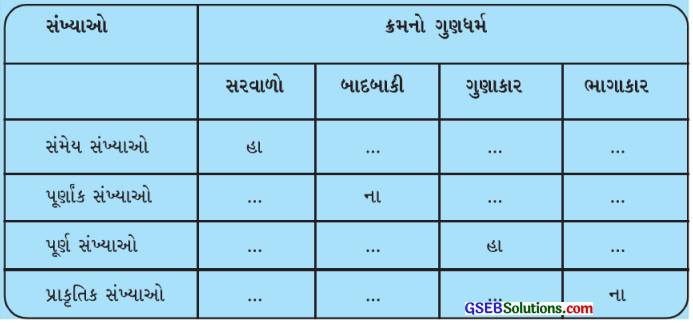
ઉત્તરઃ
આપણે સંમેય સંખ્યાઓના, પૂર્ણાંક સંખ્યાઓના, પૂર્ણ સંખ્યાઓના અને પ્રાકૃતિક સંખ્યાઓના સરવાળા, બાદબાકી, ગુણાકાર અને ભાગાકાર વિશે ક્રમના ગુણધર્મોનો અભ્યાસ કર્યો. તે પરથી ઉપરના કોષ્ટકમાં નીચે પ્રમાણે જવાબ લખાશે :
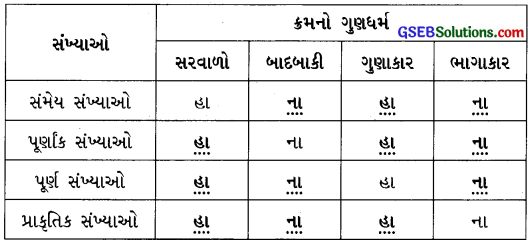
પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબ 9)
નીચેનું કોષ્ટક પૂર્ણ કરો:
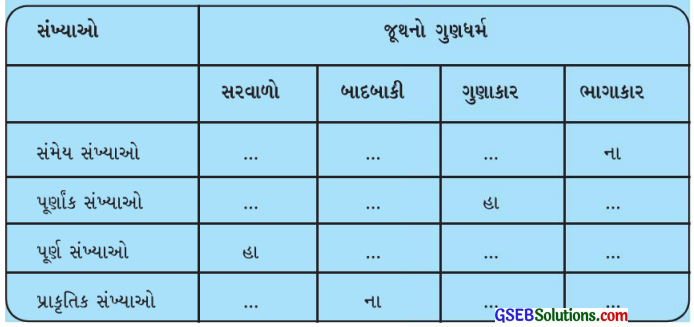
ઉત્તરઃ
આપણે સંમેય સંખ્યાઓના, પૂર્ણાંક સંખ્યાઓના, પૂર્ણ સંખ્યાઓના અને પ્રાકૃતિક સંખ્યાઓના સરવાળા, બાદબાકી, ગુણાકાર અને ભાગાકાર વિશે જૂથના ગુણધર્મોનો અભ્યાસ કર્યો. તે પરથી ઉપરના કોષ્ટકમાં પછીના પેજ પ્રમાણે જવાબ લખાશે :
![]()
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 11)
જો કોઈ ગુણધર્મ સંમેય સંખ્યા માટે સાચો હોય, તો તે પૂર્ણાંક સંખ્યા માટે પણ સાચો હોય? પૂર્ણ સંખ્યા માટે શું કહી શકાય? ક્યારે સાચો અને ક્યારે સાચો નહીં?
ઉત્તરઃ
(i) જો કોઈ ગુણધર્મ સંમેય સંખ્યા માટે સાચો હોય, તો તે પૂર્ણાંક સંખ્યા માટે પણ સાચો હોય. સિવાય કે –
‘a’ અને `b’ માટે (a ÷ b) એ પૂર્ણાક જ હોય તે જરૂરી નથી.
(ii) જો કોઈ ગુણધર્મ સંમેય સંખ્યા માટે સાચો હોય, તો તે પૂર્ણ સંખ્યા માટે પણ સાચો હોય. સિવાય કે –
(a) જો ‘a’ અને ‘b’ પૂર્ણ સંખ્યાઓ હોય, તો (a – b) એ પૂર્ણ સંખ્યા ન પણ હોય.
(b) જો ‘વ’ અને ‘b’ પૂર્ણ સંખ્યાઓ હોય, તો (b # 0), a = b એ પૂર્ણ સંખ્યા ન પણ હોય.
પ્રયત્ન કરો: (પાઠ્યપુસ્તક પાન નંબ 13)
વિભાજનના ગુણધર્મનો ઉપયોગ કરી શોધોઃ
પ્રશ્ન (i).
\(\left\{\frac{7}{5} \times\left(\frac{-3}{12}\right)\right\}+\left\{\frac{7}{5} \times \frac{5}{12}\right\}\)
ઉત્તરઃ
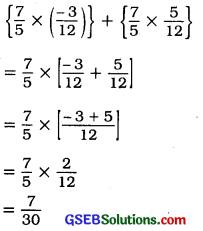
પ્રશ્ન (ii).
\(\frac {1}{2}\)
ઉત્તરઃ

![]()
પ્રયત્ન કરો (પાઠ્યપુસ્તક પાન નંબ 17)
નીચે આપેલ સંખ્યારેખામાં અંગ્રેજી મૂળાક્ષરથી દર્શાવેલ બિંદુઓને સંમેય સંખ્યાથી દર્શાવોઃ
પ્રશ્ન (i).

ઉત્તરઃ
અહીં A ને સંગત સંમેય સંખ્યા \(\frac {1}{5}\), B ને સંગત સંમેય સંખ્યા \(\frac {4}{5}\), Cને સંગત સંમેય સંખ્યા \(\frac {5}{5}\) એટલે કે 1, Dને સંગત સંમેય સંખ્યા \(\frac {8}{5}\), અને E ને સંગત સંમેય સંખ્યા \(\frac {9}{5}\) છે.

પ્રશ્ન (ii).
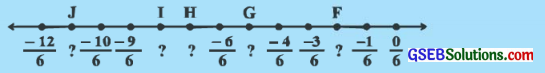
ઉત્તરઃ
અહીં F સંગત સંમેય સંખ્યા \(\frac {-2}{6}\) એટલે કે \(\frac {-1}{3}\), G ને સંગત સંમેય સંખ્યા
\(\frac {-5}{6}\), H ને સંગત સંમેય સંખ્યા \(\frac {-7}{6}\), I ને સંગત સંમેય સંખ્યા \(\frac {-8}{6}\) એટલે કે \(\frac {-4}{3}\) અને J ને સંગત સંમેય સંખ્યા \(\frac {-11}{6}\) છે.