GSEB Solutions Class 8 Maths Chapter 11 Mensuration Intext Questions

Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 11 Mensuration Intext Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 11 Mensuration Intext Questions

Try These (Page 170)

Question 1.
(a) Match the following figures with their respective areas in the box?

(b) Write the perimeter of each shape?
Solution:
(a)

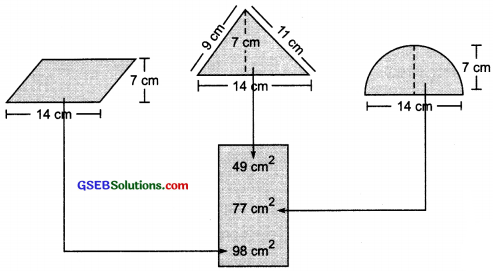
(b) (i) The given figure is a rectangle in which
Length = 14 cm
Breadth = 7 cm
∵ Perimeter of a rectangle = 2 × [Length + Breadth]
∴ Perimeter of the given figure = 2 × [14 cm + 7 cm]
= 2 × 21 cm = 42 cm

(ii) The figure is a square housing its side as 7 cm
∵ Perimeter of a square = 4 × side
∴ Perimeter of the given figure = 4 × 7 cm = 28 cm.

Try These (Page 172)

Question 1.
Nazma sister also has a trapezium shaped plot. Divide ¡tinto three parts as shown. Show that the area of trapezium WXYZ = h\(\frac{(a+b)}{2}\)

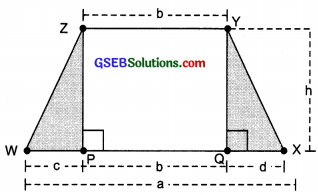
Solution:
Area of ∆ PWZ
= \(\frac{1}{2}\) × Base × Attitude = \(\frac{1}{2}\) × c × h = \(\frac{1}{2}\)ch
Area of the rectangle PQYZ = b × h = bh
Area of ∆ QXY = \(\frac{1}{2}\) × d × h = \(\frac{1}{2}\)ch
∴ Area of the trapezium XYZW

Question 2.
If h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm, find the values of each of its parts separately and add to find the area WXYZ . Verify it by putting the values of h, a and b in the expression \(\frac{h(a+b)}{2}\)?
Solution:
Area of ∆ PWZ = \(\frac{1}{2}\)ch
= \(\frac{1}{2}\) × 6 × 10cm² = 30 cm²
Area of ∆ QXY = \(\frac{1}{2}\)ch
= \(\frac{1}{2}\) × 4 × 10cm² = 20cm³
Area of rectangle PQYZ = Length × Breadth
= b × h
= 12 × 10 cm²
= 120 cm²

∴ Area of trapezium WXYZ = Area of ∆ PWZ + Area of ∆ QXY + Area of rectangle PQYZ
= 30 cm² + 20 cm² + 120 cm² = 170 cm²
Also, area of the trapezium WXYZ = \(\frac{h(a+b)}{2}\)
= \(\frac{10(22+12)}{2}\) cm² (∵a = c + b + d = 6 cm + 12 cm + 4 cm = 22 cm)
= \(\frac{10×34}{2}\) cm² = 170 cm²
Hence, the area of trapezium is verified.

Try These (Page 173)

Question 1.
Find the area of the following trapeziums?

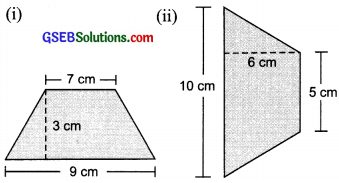
Solution:
Note: Area of a trapezium
= \(\frac{1}{2}\) × [Sum of parallel sides] × [Perpendicular distance between parallel sides]

(i) Area of the given trapezium
= \(\frac{1}{2}\) × (Sum of parallel sides) × (Perpendicular distance between parallel sides)
= \(\frac{1}{2}\) × (9 + 7) cm × 3 cm
= \(\frac{1}{2}\) × 16 cm × 3 cm = 24 cm²

(ii) Area of the given trapezium
= \(\frac{1}{2}\) × (Sum of parallel aides) × (Perpendicular distance between parallel sides)
= \(\frac{1}{2}\) × (10 + 5) cm × 6 cm
= \(\frac{1}{2}\) × 15 cm × 6 cm = 45 cm²

Try These (Page 174)

Question 1.
We know that parallelogram is also a quadrilateral. Let us also split such a quadrilateral, find their areas and hence thai of the parallelogram. Does this
agree with the formula that you know already?

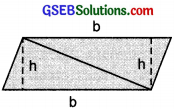
Solution:
The diagonal BD of quadrilateral ABCD is joined and it divides the quadrilateral into two traingles.

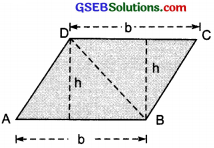
Now,
Area of quadrilateral ABCD
= Area of ∆ ABD + Area of ∆ BCD
= (\(\frac{1}{2}\) b × h) + (\(\frac{1}{2}\) b × h) = 2(\(\frac{1}{2}\) b × h) = bh
In fact ABCD is a parallelogram
∴ Area of a parallelogram ABCD = b × h
Area of a parallelogram = Base × Height
We know that a parallelogram can also be a trapezium ABCD
= \(\frac{1}{2}\) (Sum of parallel sides) × [Perpendicular distance between the parallel sides]
= \(\frac{1}{2}\) × (b + h) × h = \(\frac{1}{2}\) × (2b) × h = bh
orArea of parallelogram ABCD = bh.
Yes, the above relation agrees with formula that we know already.

Try These (Page 175)

Question 1.
Find the area of these quadrilaterals:

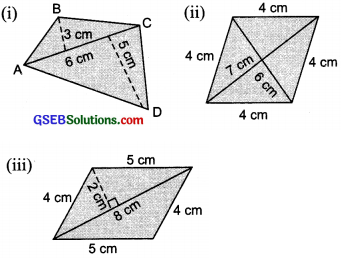
Solution:
(i) Area of quadrilateral ABCD
= \(\frac{1}{2}\) × AC × [Sum of perpendiculars on AC from opposite vertices]
= \(\frac{1}{2}\) × 6 cm × [3 cm + 5 cm]
= \(\frac{1}{2}\) × 6 cm × 8 cm = 24 cm²

(ii) The given figure is a rhombus having d₁ = 7 cm and d₂ = 6 cm.
∴ Area of the given rhombus
= \(\frac{1}{2}\) × Product of diagonals = \(\frac{1}{2}\) × d₁ × d₂
= \(\frac{1}{2}\) × 7 cm × 6 cm = 7 cm × 3 cm = 21 cm²

(iii) The given figure is a parallelogram. Its diagonal divides it into two congruent triangles.
∴ Area of the parallelogram
= 2 × [Area of one of the triangles]
= 2 × [\(\frac{1}{2}\) × 8 × 2] cm²
= 2 × 4 × 2 cm²
= 16 cm²

Try These (Page 176)

Question 1.
Divide the following polygons into parts (triangles and trapezium) to find out its area?

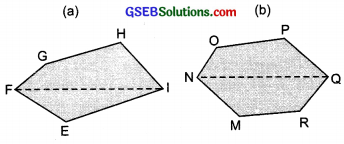
Solution:
(a) We draw perpendiculars from opposite vertices on FI. i.e. GL \(\perp\) FI, HM \(\perp\) FI and EN \(\perp\) FI
= ar (∆ GFL) + ar (trapezium GLMH) + ar (∆ HMI) + ar (∆ NEI) + ar (∆ EFN)
= (\(\frac{1}{2}\) FL × GL) + \(\frac{1}{2}\) (GL + HM) × LM + (\(\frac{1}{2}\) MI × MH) + (\(\frac{1}{2}\) NI × NE) + (\(\frac{1}{2}\) × FN × NE)

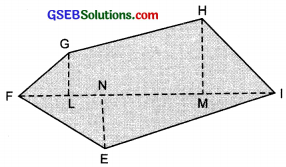
(b) NQ is a disgonal. Draw OA \(\perp\) NQ, MB \(\perp\) NQ, PC \(\perp\) NQ and RD \(\perp\) NQ

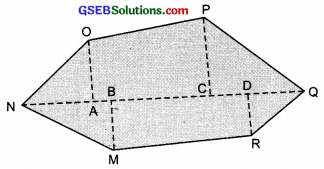
∴ Area of polygon OPQRMN
= ar (∆ OAN) + as (trap. CPOA) + ar (∆ PCQ) + ar (∆ RDQ) + ar (trap. MBDR) + ar (∆ MBN)
= (\(\frac{1}{2}\) × NA × OA) + (\(\frac{1}{2}\) × (CP + AO) × AC] + (\(\frac{1}{2}\) × CQ × PC) + (\(\frac{1}{2}\) × QD × RD) + [\(\frac{1}{2}\) × (DR + MB) × BD] + (\(\frac{1}{2}\) × BN × MB)

Question 2.
Fill in the blanks.
Poligon ABCDE is divided into pans as shown below Find its area if AD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm and perpendiculars BF = 2 cm, CH = 3 cm, EG = 2.5 cm.

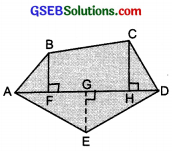
Area of polygon ABCDE = Area of ∆AFB + ………. Area of ∆AFB = \(\frac{1}{2}\) × AF × BF
= \(\frac{1}{2}\) × 3 × 2 = ……………..
Area of trapezium FBCH = FH × \(\frac{(BF+CH)}{2}\)
= 3 × \(\frac{(2+3)}{2}\) [FH = AH – AF]
Area of ∆ CHD = \(\frac{1}{2}\) × HD × CH = …………..
Area of ∆ ADE = \(\frac{1}{2}\) × AD × GE = …………….
So, the area of polygon ABCDE = ……………
Solution:
Area of polygon ABCDE = Area of ∆ AFB + Area of trapezium FBCH + Area of ∆ CHD + Area of ∆ ADE
Area of ∆ AFB = \(\frac{1}{2}\) × AF × BF
= \(\frac{1}{2}\) × 3 × 2 = 3 cm²
Area of trapezium FBCH = FH × \(\frac{BF+CH}{2}\)
= 3 × \(\frac{(2+3)}{2}\) cm² [∵ FH = AH – AF]
= 3 × \(\frac{5}{2}\) cm² = \(\frac{15}{2}\) cm² = 7.5 cm²
Area of ∆ CHD = \(\frac{1}{2}\) × HD × CH
= \(\frac{1}{2}\) × (AD – AH) × CH [∵HD = AD – AH]
= \(\frac{1}{2}\) (8 – 6) × 3 cm² = 3 cm²
Area of ∆ ADE = \(\frac{1}{2}\) × AD × GE
= \(\frac{1}{2}\) × 8 × 2.5 cm² = 4 × 2.5 cm² = 10 cm²
So, the area of polygon ABCD = 3 cm² + 7.5 cm² + 3 cm² + 10 cm² = 23.5 cm²

Question 3.
Find the area of polygon MNOPQR if MP = 9cm, MD = 7cm, MC = 6cm, MB = 4cm, MA = 2 cm. NA, OC, QD and RB are perpendiculars to diagonal MP?
Solution:
Area of polygon MNOPQR

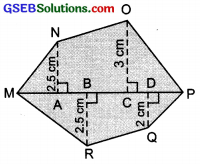
= ar (∆MAN) + ar (trap, ACON) + ar (∆CP) + ar (∆PDQ) + ar (trap. DBRQ) + ar (∆RBM)
∵ Area of ∆MAN = \(\frac{1}{2}\) × MA × AN
= \(\frac{1}{2}\) × 2 × AN cm² = AN cm²
Area of trapezium ACON = \(\frac{1}{2}\) (AN + OC) × AC

Area of ∆OCP = \(\frac{1}{2}\) × CP × OC

Area of ∆PDQ = \(\frac{1}{2}\) × PD × DQ

Area of trapezium DBRQ

Area of ∆RBM = \(\frac{1}{2}\) × MB × BR
= \(\frac{1}{2}\) × 4 × BR cm² = 2BR cm²
∴ Area of polygon MNOPQR

Try These (Page 181)

Question 1.
Find the total surface area of the following cuboids?

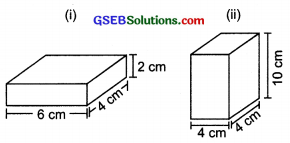
Solution:
(i) ∵ l = 6 cm, b = 4 cm and h = 2 cm
∴ Total surface area of the cuboids
= 2(lb + bh + hl)
= 2(6 × 4 + 4 × 2 + 2 × 6) cm²
= 2(24 + 8 + 12) cm²
= 2 × 44 cm² = 88 cm²

(ii) ∵ l = 4cm, b = 4 cm and h = 10 cm
∴ Total surface area of the cuboid
= 2(lb + bh + hl)
= 2(4 × 4 + 4 × 10 + 10 × 4) cm²
= 2(16 + 40 + 40) cm²
= 2 × 96 cm² = 192 cm²

Try These (Page 182)

Question 1.
Find the surface area of cube A and lateral surface area of cube B?

Solution:
For cube A:
Side (l) = 10 cm
∴ Total surface area of the cube = 6l²
= 6 × (10)² cm² = 600 cm²

For cube B:
Side (l) = 8 cm
∴ Total surface area of the cube = 6l²
= 6 × (8)² cm²
= 6 × 64 cm²
= 384 cm²

Try These (Page 184)

Question 1.
Note that lateral surface area of a cylinder is the circumference of base × height of cylinder. Can we write lateral surface area of a cuboid as perimeter of base × height of cuboid?
Solution:

Yes. Because the lateral surface area of cuboid is the surface area of its n walls, which is given by [perimeter of the room] × height.

Try These (Page 188)

Question 1.
Find the volume of the following cuboids?

Solution:
(i) Base area = 8 cm × 3 cm
Height = 2 cm
∴ Volume of the cuboid
(8 cm × 3 cm) × 2 cm = 48 cm³

(ii) Base area = 24 m²
Height = 3 cm
∴ Volume of the cuboid = Base area × height
= 24 m² × 3 cm = 24 × \(\frac{3}{100}\) m³
= \(\frac{72}{100}\) m³ = 0.72 m³
Cube: Cube is a special case of a cuboid such that its Length = Breadth = Height
∴ Its volume = Edge × Edge × Edge
Volume of a cube = (Edge)³

Question 2.
Find the volume of the following cubes (a) with a side 4 cm and (b) with a side 1.5 m?
Solution:
(a) Side (edge) of the cube = 4 cm
∴ Volume of the cube = (Edge)³ = (4 cm)³
= 4 × 4 × 4 cm³ 64 cm³

(b) Side (edge) of the cube = 1.5 m
∴ Volume of the cube = (Edge)³
= (1.5 m)³ = (\(\frac{15}{10}\) × \(\frac{15}{10}\) × \(\frac{15}{10}\))m³
= \(\frac{3375}{1000}\)m³ = 3.375m³

Try These (Page 189)

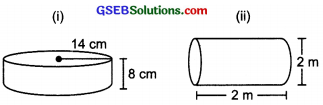
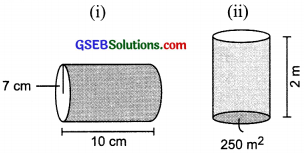
Question 1.
Find the volume of the following cylinders?

Solution:
(i) Radius (r) = 7 cm
Height (h) = 10 cm
∴ Volume of the cylinder = πr²h
= \(\frac{22}{7}\) × 7² × 10 cm³
= \(\frac{22}{7}\) × 7 × 7 × 10 cm³
= 22 × 7 × 10 cm³ = 1540 cm³

(ii) Base area 250 m², Height = 2 m
∴ Volume of the cylinder
= Base area × Height
250 m² × 2 m = 500 m³