GSEB Solutions Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1

Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1

Question 1.
Solve the following equations.
(i) x- 2 = 7
(ii) y + 3 = 10
(iii) 6 = z + 2
(iv) \(\frac { 3 }{ 7 }\) + = \(\frac { 17 }{ 7 }\)
(v) 6x = 12
(vi) \(\frac { t }{ 5 }\) = 10
(vii) \(\frac { 2x }{ 3 }\) = 18
(viii) 1.6 = \(\frac { y }{ 1.5 }\)
(ix) 7x – 9 = 16
(x) 14y – 8 = 13
(xi) 17 + 6p = 9
(xii) \(\frac { x }{ 3 }\) + 1 = \(\frac { 7 }{ 15 }\)
Solutions:
(i) x- 2 = 7
Transposing (-2) to RHS, we have
x = 7 + 2
∴ x = 9

(ii) y + 3 = 10
Transposing 3 to RHS, we have
y = 10 – 3
∴ y = 7

(iii) 6 = z + 2
Transposing 2 to LHS, we have
6 – 2 = z
or 4 = z
∴ z = 4

(iv) \(\frac { 3 }{ 7 }\) + = \(\frac { 17 }{ 7 }\)
Transposing \(\frac { 3 }{ 7 }\) to RHS, we have
x = \(\frac { 17 }{ 7 }\) – \(\frac { 3 }{ 7 }\) = \(\frac { 17 – 3 }{ 7 }\) = \(\frac { 14 }{ 7 }\) = 2
∴ x = 2

(v) 6x = 12
Dividing both sides by 6, we have:
\(\frac { 6x }{ 6 }\) = \(\frac { 12 }{ 6 }\) or x = 2
∴ x = 2

(vi) \(\frac { t }{ 5 }\) = 10
Multiplying both sides by 5, we have
\(\frac { t }{ 5 }\) ×5 = 10 ×5 or t = 50
∴ t = 50

(vii) \(\frac { 2x }{ 3 }\) = 18
Multiplying both sides by 3, we have
(\(\frac { t }{ 5 }\)) × 3 = 18 × 3 or 2x = 54
Dividing both sides by 2, we have
\(\frac { 2x }{ 2 }\) = \(\frac { 54 }{ 2 }\)
or x = \(\frac { 54 }{ 2 }\) = 27
∴ x = 27

(viii) 1.6 = \(\frac { y }{ 1.5 }\)
Multiplying both sides by 1.5, we have

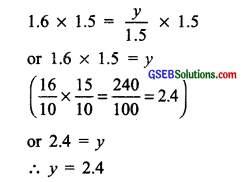
(ix) 7x – 9 = 16
Transposing (-9) to RHS, we have
7x = 16 + 9 = 25
Dividing both sides by 7, we have \(\frac { 7x }{ 7 }\) = \(\frac { 25 }{ 7 }\)
∴ x = \(\frac { 25 }{ 7 }\)

(x) 14y – 8 = 13
Transposing -8 to RHS, we have
14y = 13 + 8 = 21
Dividing both sides by 14, we have
\(\frac { 14y }{ 14 }\) or y = \(\frac { 21 }{ 14 }\) = \(\frac { 3 }{ 4 }\)
∴ y = \(\frac { 3 }{ 2 }\)

(xi) 17 + 6p = 9
Transposing 17 to RHS, we have
6p = 9 – 17 = -8
Dividing both sides by 6, we have
\(\frac { 6p }{ 6 }\) = \(\frac { -8 }{ 6 }\) or p = \(\frac { -8 }{ 6 }\) = –\(\frac { 4 }{ 3 }\)
∴ p = \(\frac { 4 }{ 3 }\)

(xii) \(\frac { x }{ 3 }\) + 1 = \(\frac { 7 }{ 15 }\)
Transposing 1 to RHS, we have
\(\frac { x }{ 3 }\) = \(\frac { 7 }{ 15 }\) – 1
or \(\frac { x }{ 3 }\) = \(\frac { 7 – 15 }{ 15 }\) = \(\frac { -8 }{ 15 }\)

Multiplying both sides by 3, we have
\(\frac { x }{ 3 }\) ×3 = \(\frac { -8 }{ 15 }\) ×3 = – \(\frac { -8 }{ 5 }\)
∴ x = \(\frac { -8 }{ 15 }\)