Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.4 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.4
Question 1.
Amina thinks of a number and subtracts \(\frac { 5 }{ 2 }\) from it. She multiplies the result by 8. The result now obtained is 3 times the same number she thought of. What is the number?
Solution:
Let the number be ‘x’.
Subtracting \(\frac { 5 }{ 2 }\), we get x – \(\frac { 5 }{ 2 }\).
According to the condition, we have
8 × (x – \(\frac { 5 }{ 2 }\)) = 3 × x or 8x – 20 = 3x
Transposing -20 to RHS, we have
8x = 3x + 20
Again transposing 3x to LHS, we have
8x – 3x = 20 or 5x = 20 or x = \(\frac { 20 }{ 5 }\) = 4
Thus, the required number = 4
![]()
Question 2.
A positive number is 5 times another number. If 21 is added to both the numbers, then one of the new numbers becomes twice the other new number. What are the numbers?
Solution:
Let the positive number = 5x
The other number = x
On adding 21 to both numbers, we get (5x + 21) and (x + 21)
According to the condition, we have
2 × (x + 21) = 5x + 21 or 2x + 42= 5x + 21
Transposing 42 to RHS, we have
2x = 5x + 21 – 42
Transposing 5x to LHS, we have
2x – 5x = -21 or – 3x = -21
Dividing both sides by (-3), we have
\(\frac { -3x }{ -3 }\) = \(\frac { -21 }{ -3 }\) or x = 7 and 5x = 5 × 7 = 35
Thus, the required numbers are 7 and 35.
![]()
Question 3.
Sum of the digits of a two-digit number is 9. When we interchange the digits, it is found that the resulting new number is greater than the original number by 27. What is the two-digit number?
Solution:
Let the units digit = x
∴ The tens digits = (9 – x)
∴ The original number = 10(9 – x) + x
= 90 – 10x + x = 90 – 9x
On interchanging the digits, the new number
= 10x + (9 – x) = 10x + 9- x = 9x + 9
According to the condition, we have
[New number] = [Original number] + 27
or 9x + 9 = 90 – 9x + 27
or 9x + 9 = 117 – 9x
or 9x = 117 – 9 – 9x [Transposing 9 to RHS]
or 9x + 9x = 108 [Transposing (-9x) to LHS]
or 18x = 108
Dividing both sides by 18, we have
x = \(\frac { 108 }{ 18 }\) = 6
∴The Original number = 90 – (9×6)
= 90 – 54 = 36
Question 4.
One of the two digits of a two-digit number is three times the other digit. If you interchange the digits of this two-digit number and add the resulting number to the original number, you get 88. What is the original number?
Solution:
Let the digit at unit place = x
The digit at tens place = 3x
The number = 10(3x) + x = 30x + x = 31x
On interchanging the digits, the number
= 10x + 3x = 13x
According to the condition, we have
31x + 13x = 88 or 44x = 88
Dividing both sides by 44, we have
\(\frac { 44x }{ 44 }\) = \(\frac { 88 }{ 44 }\) or x = 2
∴The number = 31 x 2 = 62
![]()
Question 5.
Shobo’s mother’s present age is six times Shobo’s present age. Shobo s age five years from now will be one-third of his mother s present age. What are their present ages?
Solution:
Let Shobo’s present age = x years /. Mother’s present age = 6x years After 5 years: Shobo’s age = (x + 5) years Mother’s age = (6x + 5) years According to the condition, we have
(Mother’s present age) = (Shobo’s age after 5 years)
ie. \(\frac { 1 }{ 3 }\) (6x) = x + 5 or \(\frac { 1 }{ 3 }\) × 6x = x + 5
or 2x = x + 5 or 2x – x = 5
(Transporting x to LHS)
or x = 5
∴ Shobo’s present age = 6 × 5 = 30 years
Question 6.
There is a narrow rectangular plot, reserved for a school, in Mahuli village. The length and breadth of the plot are in the ratio 11: 4. At the rate ₹ 100 per metre it will cost the village panchayat ₹ 75000 to fence the plot. What are the dimensions of the plot?
Solution:
Let the length = 11x metres and breadth = 4x metres
∴Perimeter = 2(Length + Breadth)
= 2(11x + 4x) = 2 x 15x = 30x
Cost of fencing = ₹ 100 x 30x = ₹ 3000x
But the cost of fencing is ₹ 75000.
3000x = 75000. or x = \(\frac { 75000 }{ 3000 }\) = 25
Length = 11 x 25 = 275 metres
Breadth = 4 x 25 = 100 metres
![]()
Question 7.
Hasan buys two kinds of cloth materials for school uniforms, shirt material that costs him 750 per metre and trouser material that costs him₹ 90 per metre. For every 3 metres of the shirt material, he buys 2 metres of the trouser material. He sells the materials at 12% and 10% profit respectively. His total sale is ₹ 36,600. How much trouser material did he buy?
Solution:
Let the length of cloth for trousers = 2x metres
∴ The length of cloth for shirts = 3x metres
Cost of trouser’s cloth = 2x × ₹90 = ₹ 180x
Cost of shirt’s cloth = 3x × ₹ 50 = ₹ 150x
S.P. of trouser’s cloth at 10% profit =
= ₹ \(\frac { 110 }{ 100 }\) ×108x = ₹ 198x
S.p of shirt’s clth at 12% profit = ₹ \(\frac { 112 }{ 100 }\) × 150x = ₹ 168x
∴ Total S.P = ₹ 198x + ₹ 198x = ₹366x
But the total S.P = ₹36,600
∴ 366x = 36,600 or x = \(\frac { 36600 }{ 366 }\)
[Dividing both sides by 366] = 100
∴ 2x = 2 × 100 = 200
Thus, he bougth cloth for trouser = 200 metres
Question 8.
Half of a herd of deer are grazing in the field and three-fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.
Solution:
Let the total number of deer = x
∴ Number of deer: Grazing in the field = \(\frac { x }{ 2 }\)
Playing nearly = \(\frac { 3 }{ 4 }\) × (Remaining no. of deer)
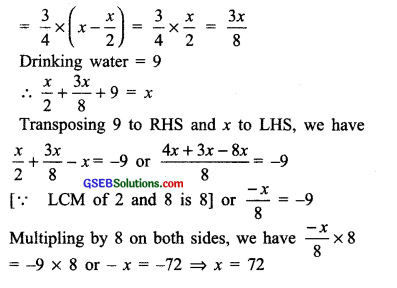
Thus, number of deer in herd = 72
![]()
Question 9.
A grandfather is ten times older than his granddaughter. He is also 54 years older than her. Find their present ages.
Solution:
Let the present age of grandfather = x years
∴Present age of granddaughter = \(\frac { 1 }{ 2 }\) years
According to the condition, we have [Present age of granddaughter] + 54 = x or \(\frac { x }{ 10 }\) + 54 = x
Transposing 54 to RHS and x to LHS, we have

Present age of grandfather = 60 years
∴Present age of granddaughter = 6 years
![]()
Question 10.
Atnan’s age is three times his son s age. Ten years ago he was five times his son’s age. Find their present ages.
Solution:
Let present age of son = x years Present age of Aman = 3x years Ten years ago son’s age = (x – 10) years Aman’s age = (3x – 10) years According to the condition, we have [Son’s age (10 years ago)] x 5 = [Aman’s age (10 years ago)] or (x – 10) x 5 = (3x – 10) or 5x – 50 = 3x – 10
Transposing (-50) to RHS and 3x to LHS, we have
5x – 3x = -10 + 50
or 2x = 40 or x = \(\frac { 40 }{ 2 }\) = 20
[Dividing both sides by 2]
and 3x = 3 × 20 = 60
Son’s present age = 20 years
Aman’s present age = 60 years